Menu Close

If-180-show-that-cos-2-cos-2-cos-2-4-cos-4-cos-4-cos-4-

Tinku Tara 0 Comments
Pin




Question Number 57873 by 786786AM last updated on 13/Apr/19
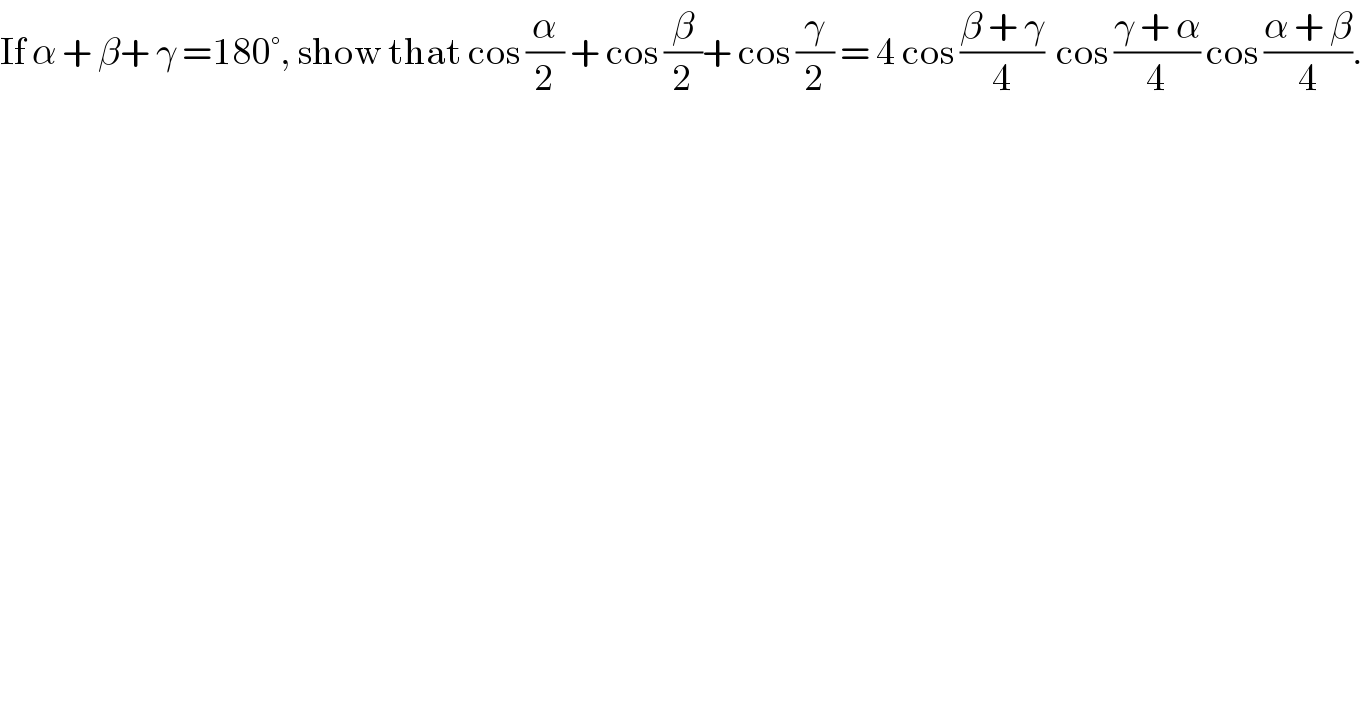
If α + β+ γ =180°, show that cos (α/2) + cos (β/2)+ cos (γ/2) = 4 cos ((β + γ)/4) cos ((γ + α)/4) cos ((α + β)/4).
$$\mathrm{If}\:\alpha\:+\:\beta+\:\gamma\:=\mathrm{180}°,\:\mathrm{show}\:\mathrm{that}\:\mathrm{cos}\:\frac{\alpha}{\mathrm{2}}\:+\:\mathrm{cos}\:\frac{\beta}{\mathrm{2}}+\:\mathrm{cos}\:\frac{\gamma}{\mathrm{2}}\:=\:\mathrm{4}\:\mathrm{cos}\:\frac{\beta\:+\:\gamma}{\mathrm{4}}\:\:\mathrm{cos}\:\frac{\gamma\:+\:\alpha}{\mathrm{4}}\:\mathrm{cos}\:\frac{\alpha\:+\:\beta}{\mathrm{4}}. \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 13/Apr/19
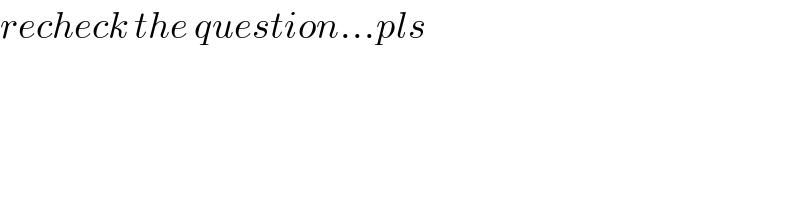
recheck the question...pls
$${recheck}\:{the}\:{question}…{pls} \\ $$
Answered by math1967 last updated on 14/Apr/19
cos(α/2) +cos(β/2)+cos(γ/2) =2cos((α+β)/4)cos((α−β)/4)+cos(((180)/2)−((α+β)/2)) =2cos((α+β)/4)cos((α−β)/4) +sin((α+β)/2) =2cos((α+β)/4)cos((α−β)/4) +2sin((α+β)/4)cos((α+β)/4) =2cos((α+β)/4){cos((α−β)/4) +sin((α+β)/4)} =2cos((α+β)/4){cos((α−β)/4) +cos(90−((α+β)/4)} =2cos((α+β)/4){2cos((90+((α−β)/4)−((α+β)/4))/2)cos((90−((α+β)/4)−((α−β)/4))/2) =2cos((α+β)/4){2cos((90−((2β)/4))/2)cos((90−((2α)/4))/2)} =4cos((α+β)/4)cos((180−β)/4)cos((180−α)/4) =4cos((α+β)/4)cos((α+γ)/4)cos((β+γ)/4) ★ ★(180−α)=β+γ,(180−β)=α+γ
$${cos}\frac{\alpha}{\mathrm{2}}\:+{cos}\frac{\beta}{\mathrm{2}}+{cos}\frac{\gamma}{\mathrm{2}} \\ $$$$=\mathrm{2}{cos}\frac{\alpha+\beta}{\mathrm{4}}{cos}\frac{\alpha−\beta}{\mathrm{4}}+{cos}\left(\frac{\mathrm{180}}{\mathrm{2}}−\frac{\alpha+\beta}{\mathrm{2}}\right) \\ $$$$=\mathrm{2}{cos}\frac{\alpha+\beta}{\mathrm{4}}{cos}\frac{\alpha−\beta}{\mathrm{4}}\:+{sin}\frac{\alpha+\beta}{\mathrm{2}} \\ $$$$=\mathrm{2}{cos}\frac{\alpha+\beta}{\mathrm{4}}{cos}\frac{\alpha−\beta}{\mathrm{4}}\:+\mathrm{2}{sin}\frac{\alpha+\beta}{\mathrm{4}}{cos}\frac{\alpha+\beta}{\mathrm{4}} \\ $$$$=\mathrm{2}{cos}\frac{\alpha+\beta}{\mathrm{4}}\left\{{cos}\frac{\alpha−\beta}{\mathrm{4}}\:+{sin}\frac{\alpha+\beta}{\mathrm{4}}\right\} \\ $$$$=\mathrm{2}{cos}\frac{\alpha+\beta}{\mathrm{4}}\left\{{cos}\frac{\alpha−\beta}{\mathrm{4}}\:+{cos}\left(\mathrm{90}−\frac{\alpha+\beta}{\mathrm{4}}\right\}\right. \\ $$$$=\mathrm{2}{cos}\frac{\alpha+\beta}{\mathrm{4}}\left\{\mathrm{2}{cos}\frac{\mathrm{90}+\frac{\alpha−\beta}{\mathrm{4}}−\frac{\alpha+\beta}{\mathrm{4}}}{\mathrm{2}}{cos}\frac{\mathrm{90}−\frac{\alpha+\beta}{\mathrm{4}}−\frac{\alpha−\beta}{\mathrm{4}}}{\mathrm{2}}\right. \\ $$$$=\mathrm{2}{cos}\frac{\alpha+\beta}{\mathrm{4}}\left\{\mathrm{2}{cos}\frac{\mathrm{90}−\frac{\mathrm{2}\beta}{\mathrm{4}}}{\mathrm{2}}{cos}\frac{\mathrm{90}−\frac{\mathrm{2}\alpha}{\mathrm{4}}}{\mathrm{2}}\right\} \\ $$$$=\mathrm{4}{cos}\frac{\alpha+\beta}{\mathrm{4}}{cos}\frac{\mathrm{180}−\beta}{\mathrm{4}}{cos}\frac{\mathrm{180}−\alpha}{\mathrm{4}} \\ $$$$=\mathrm{4}{cos}\frac{\alpha+\beta}{\mathrm{4}}{cos}\frac{\alpha+\gamma}{\mathrm{4}}{cos}\frac{\beta+\gamma}{\mathrm{4}}\:\bigstar \\ $$$$\bigstar\left(\mathrm{180}−\alpha\right)=\beta+\gamma,\left(\mathrm{180}−\beta\right)=\alpha+\gamma \\ $$
Commented by 786786AM last updated on 14/Apr/19
Tk yu sir.
$$\mathrm{Tk}\:\mathrm{yu}\:\mathrm{sir}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *