Question Number 83941 by john santu last updated on 08/Mar/20
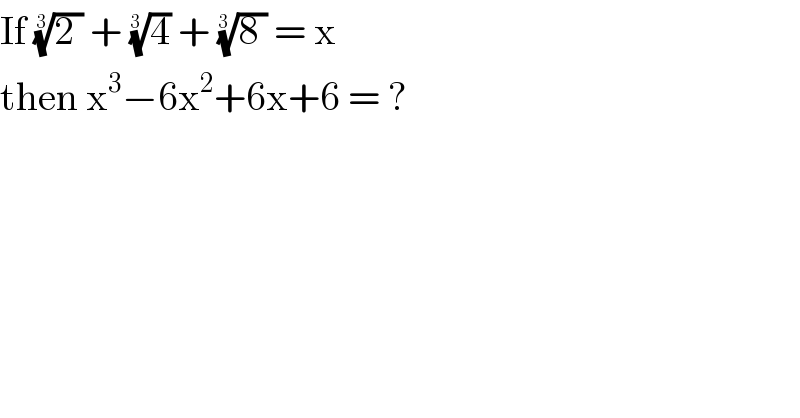
$$\mathrm{If}\:\sqrt[{\mathrm{3}}]{\mathrm{2}\:}\:+\:\sqrt[{\mathrm{3}\:}]{\mathrm{4}}\:+\:\sqrt[{\mathrm{3}\:}]{\mathrm{8}\:}\:=\:\mathrm{x}\: \\ $$$$\mathrm{then}\:\mathrm{x}^{\mathrm{3}} −\mathrm{6x}^{\mathrm{2}} +\mathrm{6x}+\mathrm{6}\:=\:? \\ $$
Answered by $@ty@m123 last updated on 08/Mar/20
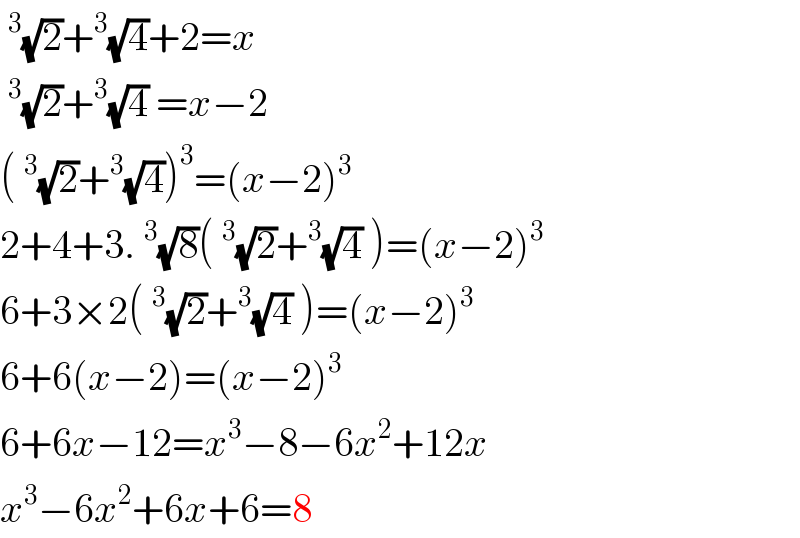
$$\:^{\mathrm{3}} \sqrt{\mathrm{2}}+^{\mathrm{3}} \sqrt{\mathrm{4}}+\mathrm{2}={x} \\ $$$$\:^{\mathrm{3}} \sqrt{\mathrm{2}}+^{\mathrm{3}} \sqrt{\mathrm{4}}\:={x}−\mathrm{2} \\ $$$$\left(\:^{\mathrm{3}} \sqrt{\mathrm{2}}+^{\mathrm{3}} \sqrt{\mathrm{4}}\right)^{\mathrm{3}} =\left({x}−\mathrm{2}\right)^{\mathrm{3}} \\ $$$$\mathrm{2}+\mathrm{4}+\mathrm{3}.\:^{\mathrm{3}} \sqrt{\mathrm{8}}\left(\:^{\mathrm{3}} \sqrt{\mathrm{2}}+^{\mathrm{3}} \sqrt{\mathrm{4}}\:\right)=\left({x}−\mathrm{2}\right)^{\mathrm{3}} \\ $$$$\mathrm{6}+\mathrm{3}×\mathrm{2}\left(\:^{\mathrm{3}} \sqrt{\mathrm{2}}+^{\mathrm{3}} \sqrt{\mathrm{4}}\:\right)=\left({x}−\mathrm{2}\right)^{\mathrm{3}} \\ $$$$\mathrm{6}+\mathrm{6}\left({x}−\mathrm{2}\right)=\left({x}−\mathrm{2}\right)^{\mathrm{3}} \\ $$$$\mathrm{6}+\mathrm{6}{x}−\mathrm{12}={x}^{\mathrm{3}} −\mathrm{8}−\mathrm{6}{x}^{\mathrm{2}} +\mathrm{12}{x} \\ $$$${x}^{\mathrm{3}} −\mathrm{6}{x}^{\mathrm{2}} +\mathrm{6}{x}+\mathrm{6}=\mathrm{8} \\ $$
Commented by john santu last updated on 08/Mar/20

$$\mathrm{good}… \\ $$
