Question Number 149621 by mathdanisur last updated on 06/Aug/21
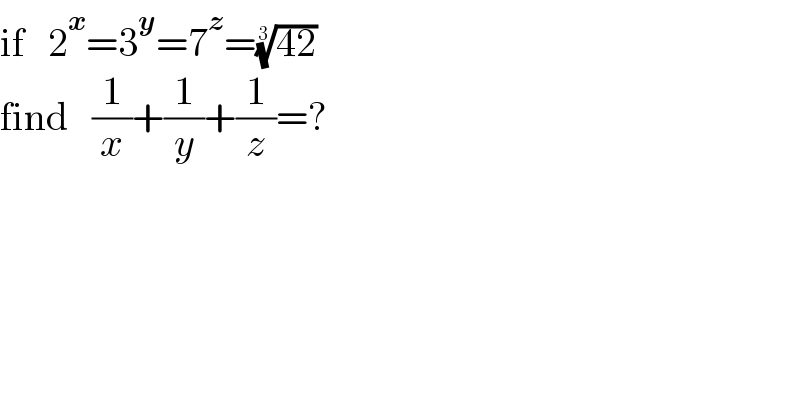
$$\mathrm{if}\:\:\:\mathrm{2}^{\boldsymbol{{x}}} =\mathrm{3}^{\boldsymbol{{y}}} =\mathrm{7}^{\boldsymbol{{z}}} =\sqrt[{\mathrm{3}}]{\mathrm{42}} \\ $$$$\mathrm{find}\:\:\:\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{y}}+\frac{\mathrm{1}}{{z}}=? \\ $$
Answered by iloveisrael last updated on 06/Aug/21
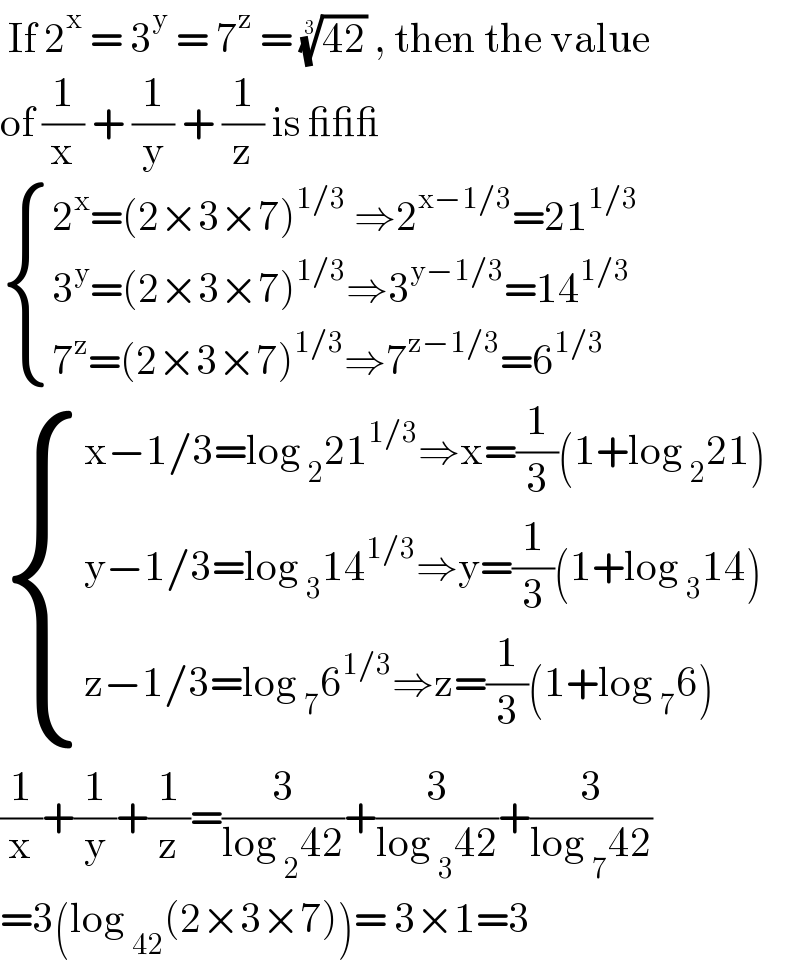
$$\:\mathrm{If}\:\mathrm{2}^{\mathrm{x}} \:=\:\mathrm{3}^{\mathrm{y}} \:=\:\mathrm{7}^{\mathrm{z}} \:=\:\sqrt[{\mathrm{3}}]{\mathrm{42}}\:,\:\mathrm{then}\:\mathrm{the}\:\mathrm{value} \\ $$$$\mathrm{of}\:\frac{\mathrm{1}}{\mathrm{x}}\:+\:\frac{\mathrm{1}}{\mathrm{y}}\:+\:\frac{\mathrm{1}}{\mathrm{z}}\:\mathrm{is}\:\_\_\_ \\ $$$$\begin{cases}{\mathrm{2}^{\mathrm{x}} =\left(\mathrm{2}×\mathrm{3}×\mathrm{7}\right)^{\mathrm{1}/\mathrm{3}} \:\Rightarrow\mathrm{2}^{\mathrm{x}−\mathrm{1}/\mathrm{3}} =\mathrm{21}^{\mathrm{1}/\mathrm{3}} }\\{\mathrm{3}^{\mathrm{y}} =\left(\mathrm{2}×\mathrm{3}×\mathrm{7}\right)^{\mathrm{1}/\mathrm{3}} \Rightarrow\mathrm{3}^{\mathrm{y}−\mathrm{1}/\mathrm{3}} =\mathrm{14}^{\mathrm{1}/\mathrm{3}} }\\{\mathrm{7}^{\mathrm{z}} =\left(\mathrm{2}×\mathrm{3}×\mathrm{7}\right)^{\mathrm{1}/\mathrm{3}} \Rightarrow\mathrm{7}^{\mathrm{z}−\mathrm{1}/\mathrm{3}} =\mathrm{6}^{\mathrm{1}/\mathrm{3}} }\end{cases} \\ $$$$\begin{cases}{\mathrm{x}−\mathrm{1}/\mathrm{3}=\mathrm{log}\:_{\mathrm{2}} \mathrm{21}^{\mathrm{1}/\mathrm{3}} \Rightarrow\mathrm{x}=\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{1}+\mathrm{log}\:_{\mathrm{2}} \mathrm{21}\right)}\\{\mathrm{y}−\mathrm{1}/\mathrm{3}=\mathrm{log}\:_{\mathrm{3}} \mathrm{14}^{\mathrm{1}/\mathrm{3}} \Rightarrow\mathrm{y}=\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{1}+\mathrm{log}\:_{\mathrm{3}} \mathrm{14}\right)}\\{\mathrm{z}−\mathrm{1}/\mathrm{3}=\mathrm{log}\:_{\mathrm{7}} \mathrm{6}^{\mathrm{1}/\mathrm{3}} \Rightarrow\mathrm{z}=\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{1}+\mathrm{log}\:_{\mathrm{7}} \mathrm{6}\right)}\end{cases} \\ $$$$\frac{\mathrm{1}}{\mathrm{x}}+\frac{\mathrm{1}}{\mathrm{y}}+\frac{\mathrm{1}}{\mathrm{z}}=\frac{\mathrm{3}}{\mathrm{log}\:_{\mathrm{2}} \mathrm{42}}+\frac{\mathrm{3}}{\mathrm{log}\:_{\mathrm{3}} \mathrm{42}}+\frac{\mathrm{3}}{\mathrm{log}\:_{\mathrm{7}} \mathrm{42}} \\ $$$$=\mathrm{3}\left(\mathrm{log}\:_{\mathrm{42}} \left(\mathrm{2}×\mathrm{3}×\mathrm{7}\right)\right)=\:\mathrm{3}×\mathrm{1}=\mathrm{3} \\ $$
Commented by mathdanisur last updated on 06/Aug/21

$$\mathrm{Thankyou}\:\boldsymbol{\mathrm{S}}\mathrm{er} \\ $$
