Question Number 113876 by Aina Samuel Temidayo last updated on 16/Sep/20
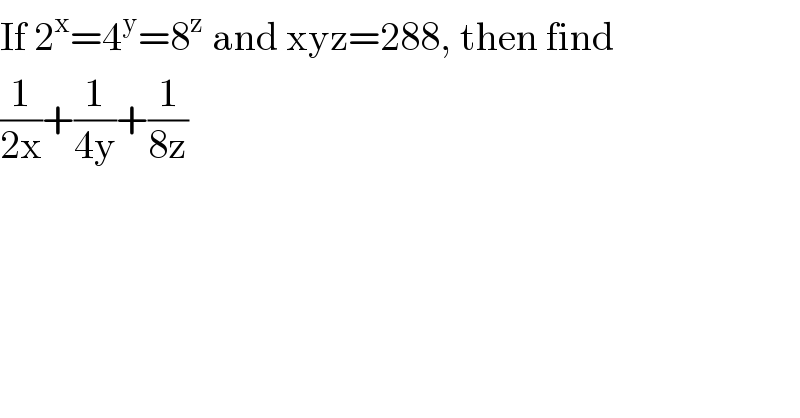
$$\mathrm{If}\:\mathrm{2}^{\mathrm{x}} =\mathrm{4}^{\mathrm{y}} =\mathrm{8}^{\mathrm{z}} \:\mathrm{and}\:\mathrm{xyz}=\mathrm{288},\:\mathrm{then}\:\mathrm{find} \\ $$$$\frac{\mathrm{1}}{\mathrm{2x}}+\frac{\mathrm{1}}{\mathrm{4y}}+\frac{\mathrm{1}}{\mathrm{8z}} \\ $$
Answered by Olaf last updated on 16/Sep/20
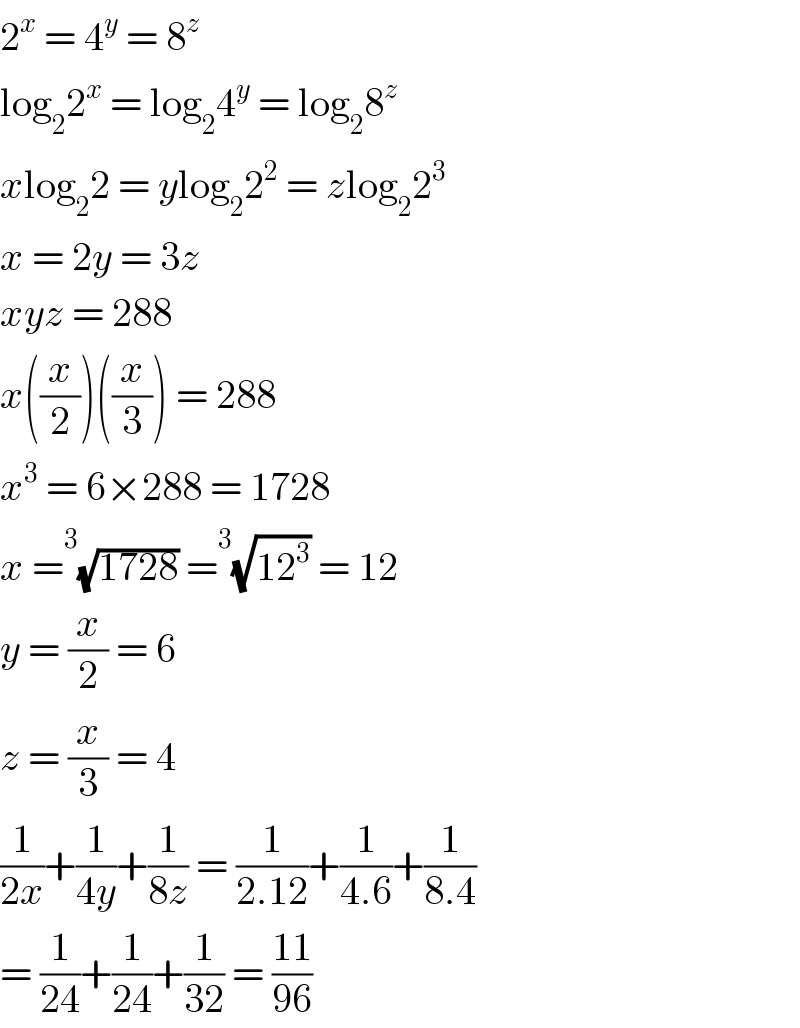
$$\mathrm{2}^{{x}} \:=\:\mathrm{4}^{{y}} \:=\:\mathrm{8}^{{z}} \\ $$$$\mathrm{log}_{\mathrm{2}} \mathrm{2}^{{x}} \:=\:\mathrm{log}_{\mathrm{2}} \mathrm{4}^{{y}} \:=\:\mathrm{log}_{\mathrm{2}} \mathrm{8}^{{z}} \\ $$$${x}\mathrm{log}_{\mathrm{2}} \mathrm{2}\:=\:{y}\mathrm{log}_{\mathrm{2}} \mathrm{2}^{\mathrm{2}} \:=\:{z}\mathrm{log}_{\mathrm{2}} \mathrm{2}^{\mathrm{3}} \\ $$$${x}\:=\:\mathrm{2}{y}\:=\:\mathrm{3}{z} \\ $$$${xyz}\:=\:\mathrm{288} \\ $$$${x}\left(\frac{{x}}{\mathrm{2}}\right)\left(\frac{{x}}{\mathrm{3}}\right)\:=\:\mathrm{288} \\ $$$${x}^{\mathrm{3}} \:=\:\mathrm{6}×\mathrm{288}\:=\:\mathrm{1728} \\ $$$${x}\:=\overset{\mathrm{3}} {\:}\sqrt{\mathrm{1728}}\:=\overset{\mathrm{3}} {\:}\sqrt{\mathrm{12}^{\mathrm{3}} }\:=\:\mathrm{12} \\ $$$${y}\:=\:\frac{{x}}{\mathrm{2}}\:=\:\mathrm{6} \\ $$$${z}\:=\:\frac{{x}}{\mathrm{3}}\:=\:\mathrm{4} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}{x}}+\frac{\mathrm{1}}{\mathrm{4}{y}}+\frac{\mathrm{1}}{\mathrm{8}{z}}\:=\:\frac{\mathrm{1}}{\mathrm{2}.\mathrm{12}}+\frac{\mathrm{1}}{\mathrm{4}.\mathrm{6}}+\frac{\mathrm{1}}{\mathrm{8}.\mathrm{4}} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{24}}+\frac{\mathrm{1}}{\mathrm{24}}+\frac{\mathrm{1}}{\mathrm{32}}\:=\:\frac{\mathrm{11}}{\mathrm{96}} \\ $$
Commented by Aina Samuel Temidayo last updated on 16/Sep/20

$$\mathrm{Thanks}. \\ $$
Answered by MJS_new last updated on 16/Sep/20
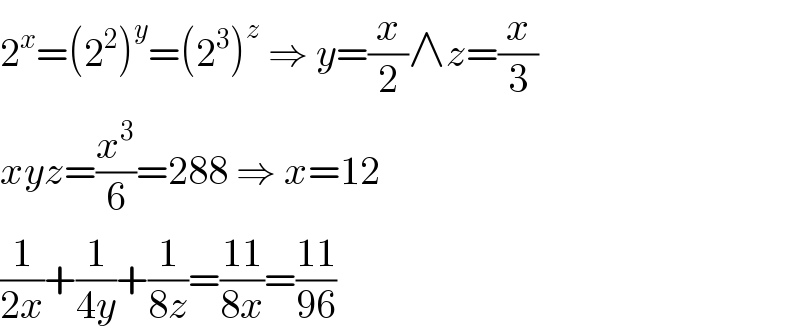
$$\mathrm{2}^{{x}} =\left(\mathrm{2}^{\mathrm{2}} \right)^{{y}} =\left(\mathrm{2}^{\mathrm{3}} \right)^{{z}} \:\Rightarrow\:{y}=\frac{{x}}{\mathrm{2}}\wedge{z}=\frac{{x}}{\mathrm{3}} \\ $$$${xyz}=\frac{{x}^{\mathrm{3}} }{\mathrm{6}}=\mathrm{288}\:\Rightarrow\:{x}=\mathrm{12} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}{x}}+\frac{\mathrm{1}}{\mathrm{4}{y}}+\frac{\mathrm{1}}{\mathrm{8}{z}}=\frac{\mathrm{11}}{\mathrm{8}{x}}=\frac{\mathrm{11}}{\mathrm{96}} \\ $$
Answered by john santu last updated on 16/Sep/20
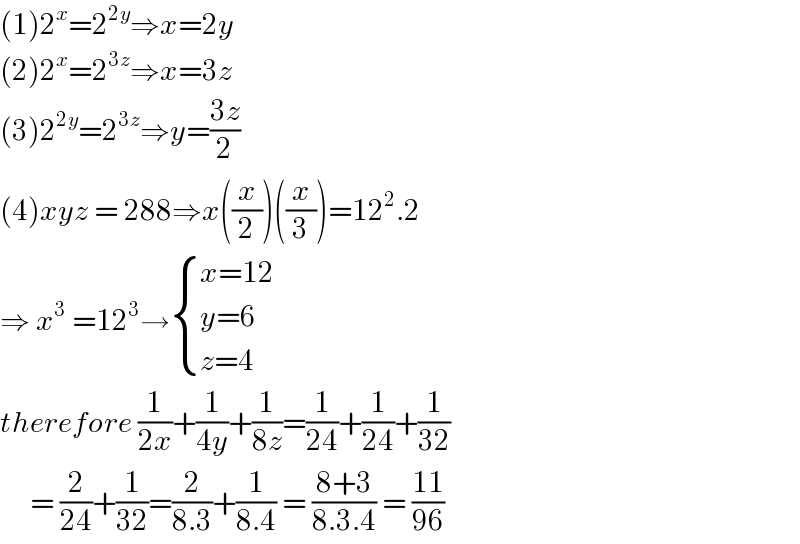
$$\left(\mathrm{1}\right)\mathrm{2}^{{x}} =\mathrm{2}^{\mathrm{2}{y}} \Rightarrow{x}=\mathrm{2}{y} \\ $$$$\left(\mathrm{2}\right)\mathrm{2}^{{x}} =\mathrm{2}^{\mathrm{3}{z}} \Rightarrow{x}=\mathrm{3}{z} \\ $$$$\left(\mathrm{3}\right)\mathrm{2}^{\mathrm{2}{y}} =\mathrm{2}^{\mathrm{3}{z}} \Rightarrow{y}=\frac{\mathrm{3}{z}}{\mathrm{2}} \\ $$$$\left(\mathrm{4}\right){xyz}\:=\:\mathrm{288}\Rightarrow{x}\left(\frac{{x}}{\mathrm{2}}\right)\left(\frac{{x}}{\mathrm{3}}\right)=\mathrm{12}^{\mathrm{2}} .\mathrm{2} \\ $$$$\Rightarrow\:{x}^{\mathrm{3}} \:=\mathrm{12}^{\mathrm{3}} \rightarrow\begin{cases}{{x}=\mathrm{12}}\\{{y}=\mathrm{6}\:}\\{{z}=\mathrm{4}}\end{cases} \\ $$$${therefore}\:\frac{\mathrm{1}}{\mathrm{2}{x}}+\frac{\mathrm{1}}{\mathrm{4}{y}}+\frac{\mathrm{1}}{\mathrm{8}{z}}=\frac{\mathrm{1}}{\mathrm{24}}+\frac{\mathrm{1}}{\mathrm{24}}+\frac{\mathrm{1}}{\mathrm{32}} \\ $$$$\:\:\:\:\:=\:\frac{\mathrm{2}}{\mathrm{24}}+\frac{\mathrm{1}}{\mathrm{32}}=\frac{\mathrm{2}}{\mathrm{8}.\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{8}.\mathrm{4}}\:=\:\frac{\mathrm{8}+\mathrm{3}}{\mathrm{8}.\mathrm{3}.\mathrm{4}}\:=\:\frac{\mathrm{11}}{\mathrm{96}} \\ $$
Commented by Aina Samuel Temidayo last updated on 16/Sep/20

$$\mathrm{Thanks}. \\ $$
Answered by floor(10²Eta[1]) last updated on 16/Sep/20
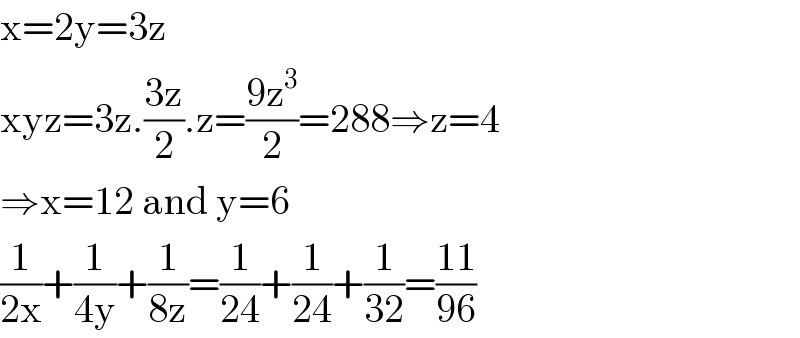
$$\mathrm{x}=\mathrm{2y}=\mathrm{3z} \\ $$$$\mathrm{xyz}=\mathrm{3z}.\frac{\mathrm{3z}}{\mathrm{2}}.\mathrm{z}=\frac{\mathrm{9z}^{\mathrm{3}} }{\mathrm{2}}=\mathrm{288}\Rightarrow\mathrm{z}=\mathrm{4} \\ $$$$\Rightarrow\mathrm{x}=\mathrm{12}\:\mathrm{and}\:\mathrm{y}=\mathrm{6} \\ $$$$\frac{\mathrm{1}}{\mathrm{2x}}+\frac{\mathrm{1}}{\mathrm{4y}}+\frac{\mathrm{1}}{\mathrm{8z}}=\frac{\mathrm{1}}{\mathrm{24}}+\frac{\mathrm{1}}{\mathrm{24}}+\frac{\mathrm{1}}{\mathrm{32}}=\frac{\mathrm{11}}{\mathrm{96}} \\ $$
