Question Number 124423 by ZiYangLee last updated on 03/Dec/20
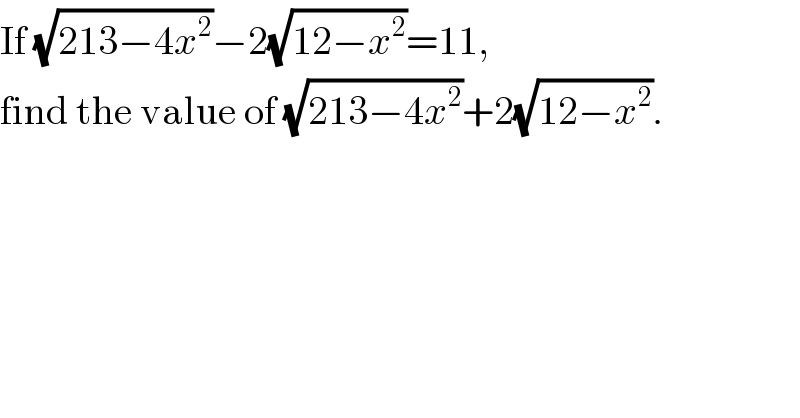
$$\mathrm{If}\:\sqrt{\mathrm{213}−\mathrm{4}{x}^{\mathrm{2}} }−\mathrm{2}\sqrt{\mathrm{12}−{x}^{\mathrm{2}} }=\mathrm{11}, \\ $$$$\mathrm{find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\sqrt{\mathrm{213}−\mathrm{4}{x}^{\mathrm{2}} }+\mathrm{2}\sqrt{\mathrm{12}−{x}^{\mathrm{2}} }. \\ $$
Commented by ZiYangLee last updated on 03/Dec/20

$$\mathrm{Answer}:\:\mathrm{15} \\ $$
Answered by Olaf last updated on 03/Dec/20

$$\sqrt{\mathrm{213}−\mathrm{4}{x}^{\mathrm{2}} }−\mathrm{2}\sqrt{\mathrm{12}−{x}^{\mathrm{2}} }\:= \\ $$$$\frac{\left(\mathrm{213}−\mathrm{4}{x}^{\mathrm{2}} \right)−\mathrm{4}\left(\mathrm{12}−{x}^{\mathrm{2}} \right)}{\:\sqrt{\mathrm{213}−\mathrm{4}{x}^{\mathrm{2}} }+\mathrm{2}\sqrt{\mathrm{12}−{x}^{\mathrm{2}} }}\:= \\ $$$$\frac{\mathrm{213}−\mathrm{4}×\mathrm{12}}{\:\sqrt{\mathrm{213}−\mathrm{4}{x}^{\mathrm{2}} }+\mathrm{2}\sqrt{\mathrm{12}−{x}^{\mathrm{2}} }}\:= \\ $$$$\frac{\mathrm{165}}{\:\sqrt{\mathrm{213}−\mathrm{4}{x}^{\mathrm{2}} }+\mathrm{2}\sqrt{\mathrm{12}−{x}^{\mathrm{2}} }}\:= \\ $$$$\frac{\mathrm{15}×\mathrm{11}}{\:\sqrt{\mathrm{213}−\mathrm{4}{x}^{\mathrm{2}} }+\mathrm{2}\sqrt{\mathrm{12}−{x}^{\mathrm{2}} }}\:=\:\mathrm{11} \\ $$$$\Rightarrow\:\sqrt{\mathrm{213}−\mathrm{4}{x}^{\mathrm{2}} }+\mathrm{2}\sqrt{\mathrm{12}−{x}^{\mathrm{2}} }\:=\:\mathrm{15} \\ $$
