Menu Close

If-2cos-sin-1-2-0-lt-lt-90-then-2sin-cos-

Tinku Tara 0 Comments
Pin




Question Number 115062 by Sudip last updated on 23/Sep/20
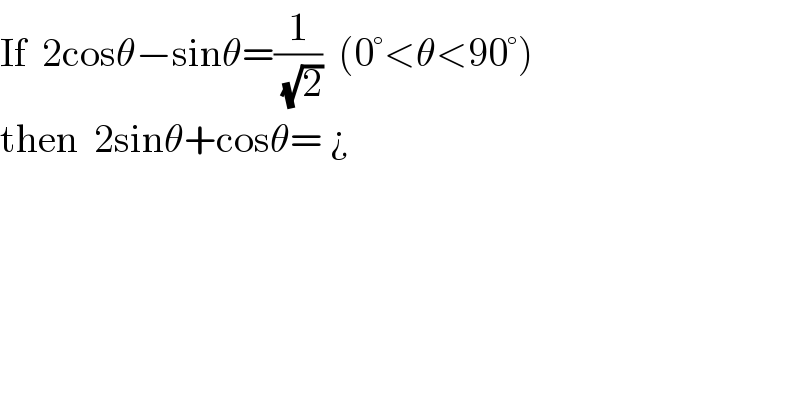
If 2cosθ−sinθ=(1/( (√2))) (0°<θ<90°) then 2sinθ+cosθ= ¿
$$\mathrm{If}\:\:\mathrm{2cos}\theta−\mathrm{sin}\theta=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:\:\left(\mathrm{0}°<\theta<\mathrm{90}°\right) \\ $$$$\mathrm{then}\:\:\mathrm{2sin}\theta+\mathrm{cos}\theta=\:¿ \\ $$
Answered by PRITHWISH SEN 2 last updated on 23/Sep/20
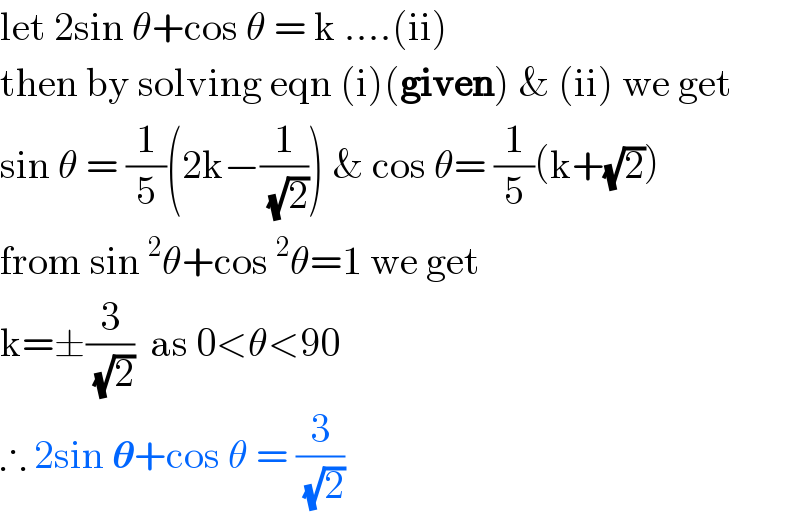
let 2sin θ+cos θ = k ....(ii) then by solving eqn (i)(given) & (ii) we get sin θ = (1/5)(2k−(1/( (√2)))) & cos θ= (1/5)(k+(√2)) from sin^2 θ+cos^2 θ=1 we get k=±(3/( (√2))) as 0<θ<90 ∴ 2sin 𝛉+cos θ = (3/( (√2)))
$$\mathrm{let}\:\mathrm{2sin}\:\theta+\mathrm{cos}\:\theta\:=\:\mathrm{k}\:….\left(\mathrm{ii}\right) \\ $$$$\mathrm{then}\:\mathrm{by}\:\mathrm{solving}\:\mathrm{eqn}\:\left(\mathrm{i}\right)\left(\boldsymbol{\mathrm{given}}\right)\:\&\:\left(\mathrm{ii}\right)\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{sin}\:\theta\:=\:\frac{\mathrm{1}}{\mathrm{5}}\left(\mathrm{2k}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)\:\&\:\mathrm{cos}\:\theta=\:\frac{\mathrm{1}}{\mathrm{5}}\left(\mathrm{k}+\sqrt{\mathrm{2}}\right) \\ $$$$\mathrm{from}\:\mathrm{sin}\:^{\mathrm{2}} \theta+\mathrm{cos}\:^{\mathrm{2}} \theta=\mathrm{1}\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{k}=\pm\frac{\mathrm{3}}{\:\sqrt{\mathrm{2}}}\:\:\mathrm{as}\:\mathrm{0}<\theta<\mathrm{90} \\ $$$$\therefore\:\mathrm{2sin}\:\boldsymbol{\theta}+\mathrm{cos}\:\theta\:=\:\frac{\mathrm{3}}{\:\sqrt{\mathrm{2}}} \\ $$
Answered by Dwaipayan Shikari last updated on 23/Sep/20
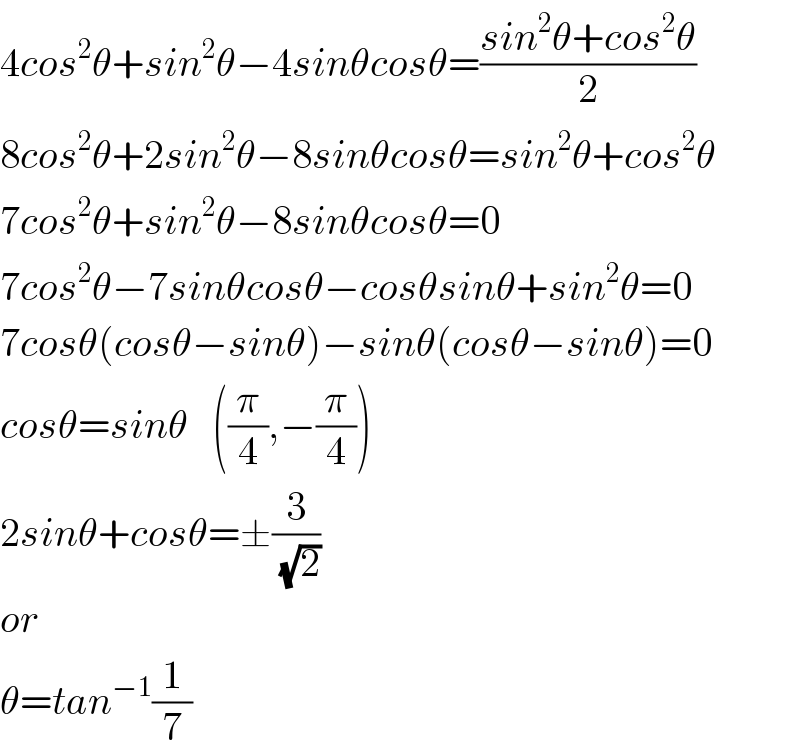
4cos^2 θ+sin^2 θ−4sinθcosθ=((sin^2 θ+cos^2 θ)/2) 8cos^2 θ+2sin^2 θ−8sinθcosθ=sin^2 θ+cos^2 θ 7cos^2 θ+sin^2 θ−8sinθcosθ=0 7cos^2 θ−7sinθcosθ−cosθsinθ+sin^2 θ=0 7cosθ(cosθ−sinθ)−sinθ(cosθ−sinθ)=0 cosθ=sinθ ((π/4),−(π/4)) 2sinθ+cosθ=±(3/( (√2))) or θ=tan^(−1) (1/7)
$$\mathrm{4}{cos}^{\mathrm{2}} \theta+{sin}^{\mathrm{2}} \theta−\mathrm{4}{sin}\theta{cos}\theta=\frac{{sin}^{\mathrm{2}} \theta+{cos}^{\mathrm{2}} \theta}{\mathrm{2}} \\ $$$$\mathrm{8}{cos}^{\mathrm{2}} \theta+\mathrm{2}{sin}^{\mathrm{2}} \theta−\mathrm{8}{sin}\theta{cos}\theta={sin}^{\mathrm{2}} \theta+{cos}^{\mathrm{2}} \theta \\ $$$$\mathrm{7}{cos}^{\mathrm{2}} \theta+{sin}^{\mathrm{2}} \theta−\mathrm{8}{sin}\theta{cos}\theta=\mathrm{0} \\ $$$$\mathrm{7}{cos}^{\mathrm{2}} \theta−\mathrm{7}{sin}\theta{cos}\theta−{cos}\theta{sin}\theta+{sin}^{\mathrm{2}} \theta=\mathrm{0} \\ $$$$\mathrm{7}{cos}\theta\left({cos}\theta−{sin}\theta\right)−{sin}\theta\left({cos}\theta−{sin}\theta\right)=\mathrm{0} \\ $$$${cos}\theta={sin}\theta\:\:\:\left(\frac{\pi}{\mathrm{4}},−\frac{\pi}{\mathrm{4}}\right) \\ $$$$\mathrm{2}{sin}\theta+{cos}\theta=\pm\frac{\mathrm{3}}{\:\sqrt{\mathrm{2}}} \\ $$$${or} \\ $$$$\theta={tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{7}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *