Menu Close

If-2f-x-f-1-x-3x-what-is-f-x-

Tinku Tara 0 Comments
Pin




Question Number 110436 by bemath last updated on 29/Aug/20
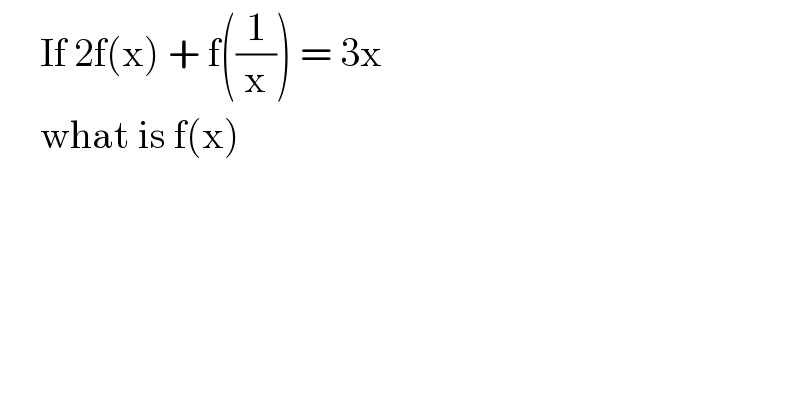
If 2f(x) + f((1/x)) = 3x what is f(x)
$$\:\:\:\:\:\mathrm{If}\:\mathrm{2f}\left(\mathrm{x}\right)\:+\:\mathrm{f}\left(\frac{\mathrm{1}}{\mathrm{x}}\right)\:=\:\mathrm{3x} \\ $$$$\:\:\:\:\:\mathrm{what}\:\mathrm{is}\:\mathrm{f}\left(\mathrm{x}\right) \\ $$
Answered by john santu last updated on 29/Aug/20
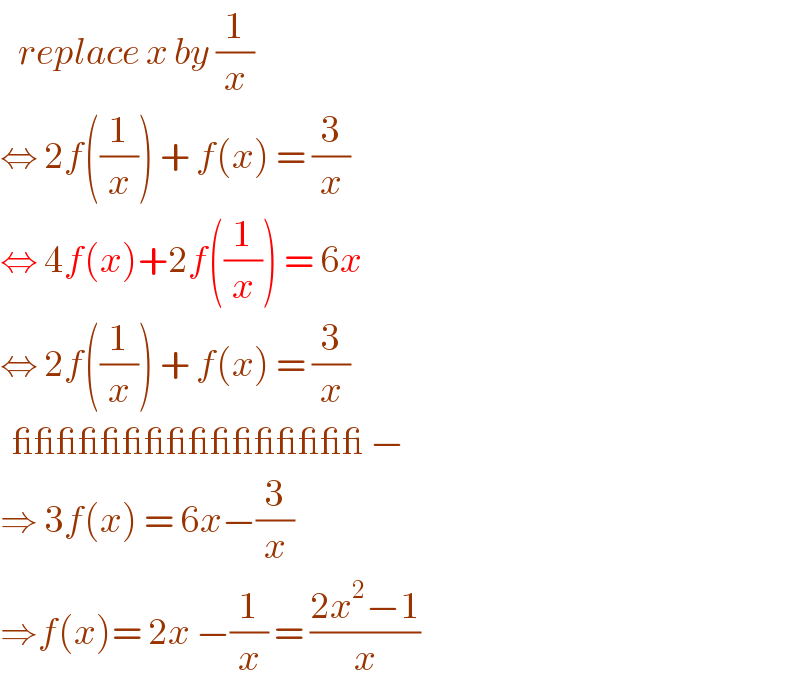
replace x by (1/x) ⇔ 2f((1/x)) + f(x) = (3/x) ⇔ 4f(x)+2f((1/x)) = 6x ⇔ 2f((1/x)) + f(x) = (3/x) ________________ − ⇒ 3f(x) = 6x−(3/x) ⇒f(x)= 2x −(1/x) = ((2x^2 −1)/x)
$$\:\:\:{replace}\:{x}\:{by}\:\frac{\mathrm{1}}{{x}} \\ $$$$\Leftrightarrow\:\mathrm{2}{f}\left(\frac{\mathrm{1}}{{x}}\right)\:+\:{f}\left({x}\right)\:=\:\frac{\mathrm{3}}{{x}}\: \\ $$$$\Leftrightarrow\:\mathrm{4}{f}\left({x}\right)+\mathrm{2}{f}\left(\frac{\mathrm{1}}{{x}}\right)\:=\:\mathrm{6}{x} \\ $$$$\Leftrightarrow\:\mathrm{2}{f}\left(\frac{\mathrm{1}}{{x}}\right)\:+\:{f}\left({x}\right)\:=\:\frac{\mathrm{3}}{{x}} \\ $$$$\:\:\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\:− \\ $$$$\Rightarrow\:\mathrm{3}{f}\left({x}\right)\:=\:\mathrm{6}{x}−\frac{\mathrm{3}}{{x}} \\ $$$$\Rightarrow{f}\left({x}\right)=\:\mathrm{2}{x}\:−\frac{\mathrm{1}}{{x}}\:=\:\frac{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{1}}{{x}} \\ $$
Answered by mathmax by abdo last updated on 29/Aug/20
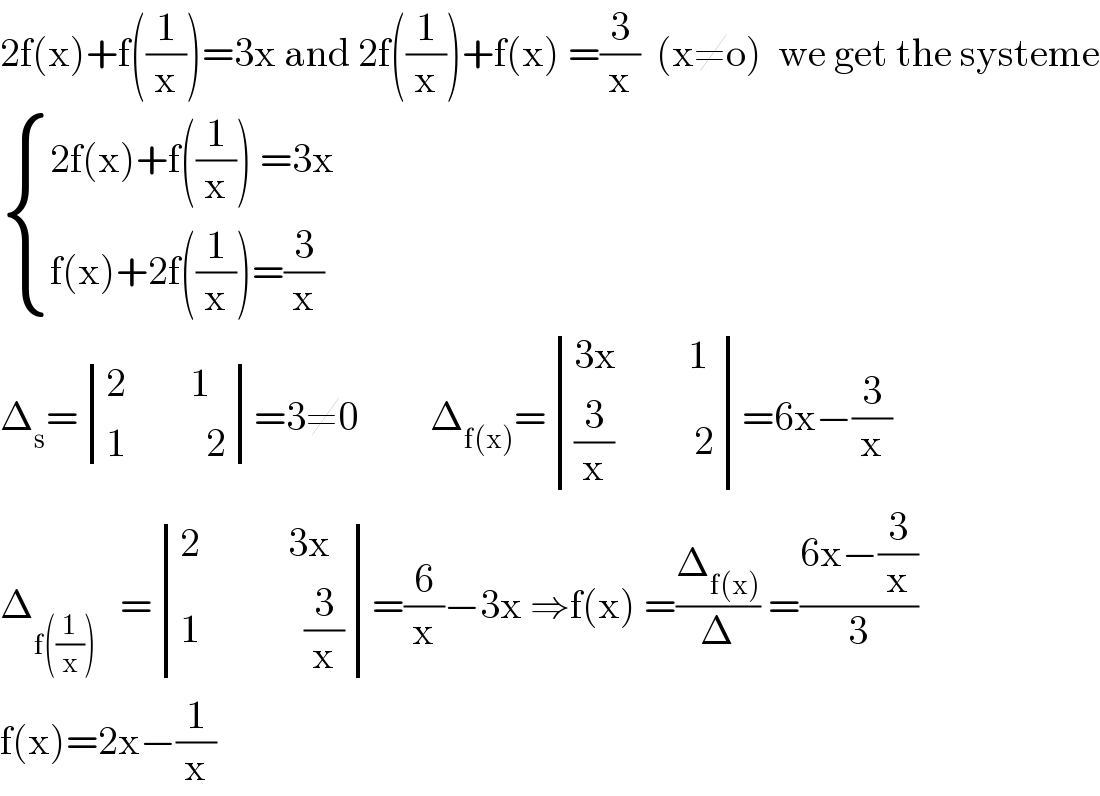
2f(x)+f((1/x))=3x and 2f((1/x))+f(x) =(3/x) (x≠o) we get the systeme { ((2f(x)+f((1/x)) =3x)),((f(x)+2f((1/x))=(3/x))) :} Δ_s = determinant (((2 1)),((1 2)))=3≠0 Δ_(f(x)) = determinant (((3x 1)),(((3/x) 2)))=6x−(3/x) Δ_(f((1/x))) = determinant (((2 3x)),((1 (3/x))))=(6/x)−3x ⇒f(x) =(Δ_(f(x)) /Δ) =((6x−(3/x))/3) f(x)=2x−(1/x)
$$\mathrm{2f}\left(\mathrm{x}\right)+\mathrm{f}\left(\frac{\mathrm{1}}{\mathrm{x}}\right)=\mathrm{3x}\:\mathrm{and}\:\mathrm{2f}\left(\frac{\mathrm{1}}{\mathrm{x}}\right)+\mathrm{f}\left(\mathrm{x}\right)\:=\frac{\mathrm{3}}{\mathrm{x}}\:\:\left(\mathrm{x}\neq\mathrm{o}\right)\:\:\mathrm{we}\:\mathrm{get}\:\mathrm{the}\:\mathrm{systeme} \\ $$$$\begin{cases}{\mathrm{2f}\left(\mathrm{x}\right)+\mathrm{f}\left(\frac{\mathrm{1}}{\mathrm{x}}\right)\:=\mathrm{3x}}\\{\mathrm{f}\left(\mathrm{x}\right)+\mathrm{2f}\left(\frac{\mathrm{1}}{\mathrm{x}}\right)=\frac{\mathrm{3}}{\mathrm{x}}}\end{cases} \\ $$$$\Delta_{\mathrm{s}} =\begin{vmatrix}{\mathrm{2}\:\:\:\:\:\:\:\:\mathrm{1}}\\{\mathrm{1}\:\:\:\:\:\:\:\:\:\:\mathrm{2}}\end{vmatrix}=\mathrm{3}\neq\mathrm{0}\:\:\:\:\:\:\:\:\:\Delta_{\mathrm{f}\left(\mathrm{x}\right)} =\begin{vmatrix}{\mathrm{3x}\:\:\:\:\:\:\:\:\:\mathrm{1}}\\{\frac{\mathrm{3}}{\mathrm{x}}\:\:\:\:\:\:\:\:\:\:\mathrm{2}}\end{vmatrix}=\mathrm{6x}−\frac{\mathrm{3}}{\mathrm{x}} \\ $$$$\Delta_{\mathrm{f}\left(\frac{\mathrm{1}}{\mathrm{x}}\right)} \:\:\:=\begin{vmatrix}{\mathrm{2}\:\:\:\:\:\:\:\:\:\:\:\mathrm{3x}}\\{\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{3}}{\mathrm{x}}}\end{vmatrix}=\frac{\mathrm{6}}{\mathrm{x}}−\mathrm{3x}\:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\:=\frac{\Delta_{\mathrm{f}\left(\mathrm{x}\right)} }{\Delta}\:=\frac{\mathrm{6x}−\frac{\mathrm{3}}{\mathrm{x}}}{\mathrm{3}} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{2x}−\frac{\mathrm{1}}{\mathrm{x}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *