Question Number 30871 by ajfour last updated on 27/Feb/18
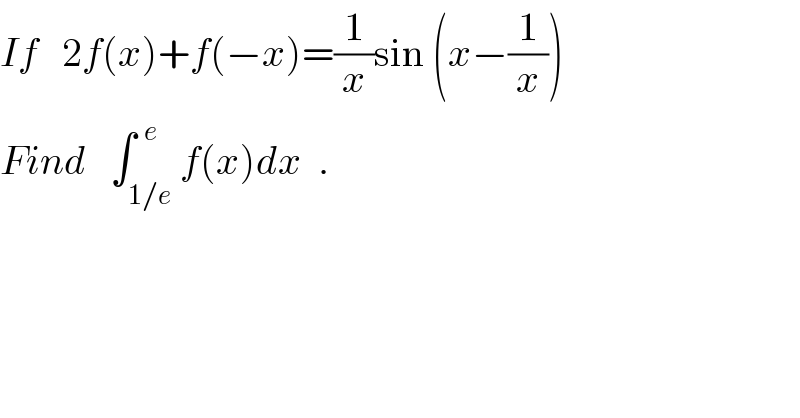
$${If}\:\:\:\mathrm{2}{f}\left({x}\right)+{f}\left(−{x}\right)=\frac{\mathrm{1}}{{x}}\mathrm{sin}\:\left({x}−\frac{\mathrm{1}}{{x}}\right) \\ $$$${Find}\:\:\:\int_{\mathrm{1}/{e}} ^{\:\:{e}} {f}\left({x}\right){dx}\:\:. \\ $$
Commented by abdo imad last updated on 27/Feb/18
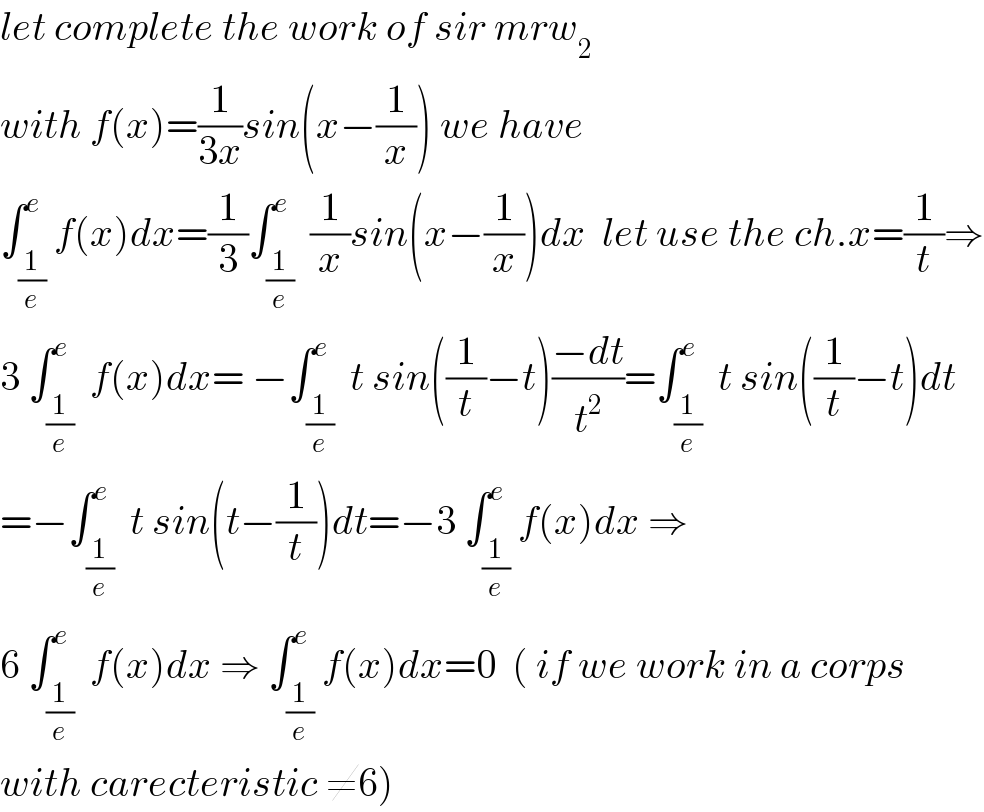
$${let}\:{complete}\:{the}\:{work}\:{of}\:{sir}\:{mrw}_{\mathrm{2}} \\ $$$${with}\:{f}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{3}{x}}{sin}\left({x}−\frac{\mathrm{1}}{{x}}\right)\:{we}\:{have} \\ $$$$\int_{\frac{\mathrm{1}}{{e}}} ^{{e}} {f}\left({x}\right){dx}=\frac{\mathrm{1}}{\mathrm{3}}\int_{\frac{\mathrm{1}}{{e}}} ^{{e}} \:\frac{\mathrm{1}}{{x}}{sin}\left({x}−\frac{\mathrm{1}}{{x}}\right){dx}\:\:{let}\:{use}\:{the}\:{ch}.{x}=\frac{\mathrm{1}}{{t}}\Rightarrow \\ $$$$\mathrm{3}\:\int_{\frac{\mathrm{1}}{{e}}} ^{{e}} \:{f}\left({x}\right){dx}=\:−\int_{\frac{\mathrm{1}}{{e}}} ^{{e}} \:{t}\:{sin}\left(\frac{\mathrm{1}}{{t}}−{t}\right)\frac{−{dt}}{{t}^{\mathrm{2}} }=\int_{\frac{\mathrm{1}}{{e}}} ^{{e}} \:{t}\:{sin}\left(\frac{\mathrm{1}}{{t}}−{t}\right){dt} \\ $$$$=−\int_{\frac{\mathrm{1}}{{e}}} ^{{e}} \:{t}\:{sin}\left({t}−\frac{\mathrm{1}}{{t}}\right){dt}=−\mathrm{3}\:\int_{\frac{\mathrm{1}}{{e}}} ^{{e}} {f}\left({x}\right){dx}\:\Rightarrow \\ $$$$\mathrm{6}\:\int_{\frac{\mathrm{1}}{{e}}} ^{{e}} \:{f}\left({x}\right){dx}\:\Rightarrow\:\int_{\frac{\mathrm{1}}{{e}}} ^{{e}} {f}\left({x}\right){dx}=\mathrm{0}\:\:\left(\:{if}\:{we}\:{work}\:{in}\:{a}\:{corps}\right. \\ $$$$\left.{with}\:{carecteristic}\:\neq\mathrm{6}\right) \\ $$
Commented by ajfour last updated on 28/Feb/18

$${Thank}\:{you}\:{Sir}. \\ $$
Answered by mrW2 last updated on 27/Feb/18
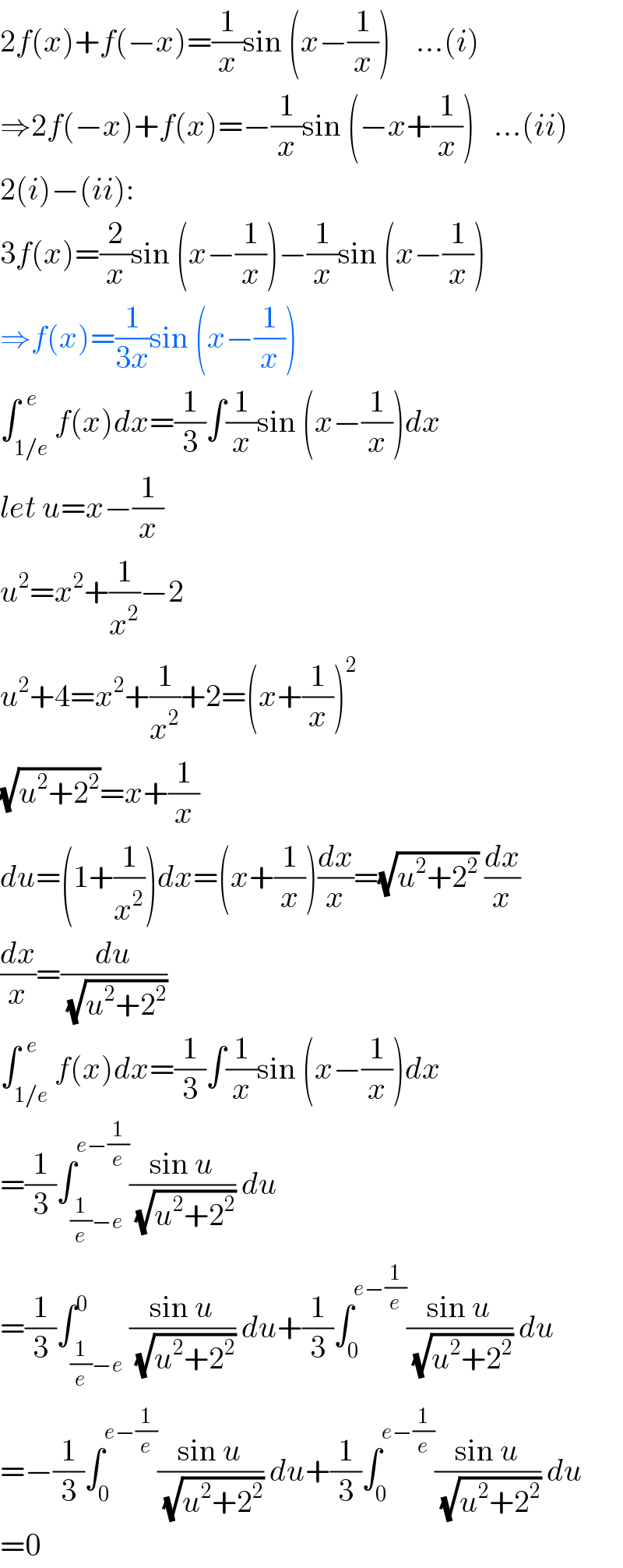
$$\mathrm{2}{f}\left({x}\right)+{f}\left(−{x}\right)=\frac{\mathrm{1}}{{x}}\mathrm{sin}\:\left({x}−\frac{\mathrm{1}}{{x}}\right)\:\:\:\:…\left({i}\right) \\ $$$$\Rightarrow\mathrm{2}{f}\left(−{x}\right)+{f}\left({x}\right)=−\frac{\mathrm{1}}{{x}}\mathrm{sin}\:\left(−{x}+\frac{\mathrm{1}}{{x}}\right)\:\:\:…\left({ii}\right) \\ $$$$\mathrm{2}\left({i}\right)−\left({ii}\right): \\ $$$$\mathrm{3}{f}\left({x}\right)=\frac{\mathrm{2}}{{x}}\mathrm{sin}\:\left({x}−\frac{\mathrm{1}}{{x}}\right)−\frac{\mathrm{1}}{{x}}\mathrm{sin}\:\left({x}−\frac{\mathrm{1}}{{x}}\right) \\ $$$$\Rightarrow{f}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{3}{x}}\mathrm{sin}\:\left({x}−\frac{\mathrm{1}}{{x}}\right) \\ $$$$\int_{\mathrm{1}/{e}} ^{\:\:{e}} {f}\left({x}\right){dx}=\frac{\mathrm{1}}{\mathrm{3}}\int\frac{\mathrm{1}}{{x}}\mathrm{sin}\:\left({x}−\frac{\mathrm{1}}{{x}}\right){dx} \\ $$$${let}\:{u}={x}−\frac{\mathrm{1}}{{x}} \\ $$$${u}^{\mathrm{2}} ={x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }−\mathrm{2} \\ $$$${u}^{\mathrm{2}} +\mathrm{4}={x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+\mathrm{2}=\left({x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} \\ $$$$\sqrt{{u}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} }={x}+\frac{\mathrm{1}}{{x}} \\ $$$${du}=\left(\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right){dx}=\left({x}+\frac{\mathrm{1}}{{x}}\right)\frac{{dx}}{{x}}=\sqrt{{u}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} }\:\frac{{dx}}{{x}} \\ $$$$\frac{{dx}}{{x}}=\frac{{du}}{\:\sqrt{{u}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} }} \\ $$$$\int_{\mathrm{1}/{e}} ^{\:\:{e}} {f}\left({x}\right){dx}=\frac{\mathrm{1}}{\mathrm{3}}\int\frac{\mathrm{1}}{{x}}\mathrm{sin}\:\left({x}−\frac{\mathrm{1}}{{x}}\right){dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\int_{\frac{\mathrm{1}}{{e}}−{e}} ^{{e}−\frac{\mathrm{1}}{{e}}} \frac{\mathrm{sin}\:{u}}{\:\sqrt{{u}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} }}\:{du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\int_{\frac{\mathrm{1}}{{e}}−{e}} ^{\mathrm{0}} \frac{\mathrm{sin}\:{u}}{\:\sqrt{{u}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} }}\:{du}+\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{{e}−\frac{\mathrm{1}}{{e}}} \frac{\mathrm{sin}\:{u}}{\:\sqrt{{u}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} }}\:{du} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{{e}−\frac{\mathrm{1}}{{e}}} \frac{\mathrm{sin}\:{u}}{\:\sqrt{{u}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} }}\:{du}+\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{{e}−\frac{\mathrm{1}}{{e}}} \frac{\mathrm{sin}\:{u}}{\:\sqrt{{u}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} }}\:{du} \\ $$$$=\mathrm{0} \\ $$
Commented by abdo imad last updated on 27/Feb/18

$${sir}\:{you}\:{are}\:{more}\:{near}\:{from}\:{value}\:{look}\:{that} \\ $$$$\frac{\mathrm{1}}{{e}}−{e}=−\left({e}−\frac{\mathrm{1}}{{e}}\right)\:{and}\:{the}\:{function}\:\:{u}\rightarrow\frac{{sinu}}{\:\sqrt{{u}^{\mathrm{2}} \:+\mathrm{4}}}\:{is}\:{odd}\:{so} \\ $$$$\int\left(…\right){du}=\mathrm{0}. \\ $$
Commented by mrW2 last updated on 27/Feb/18
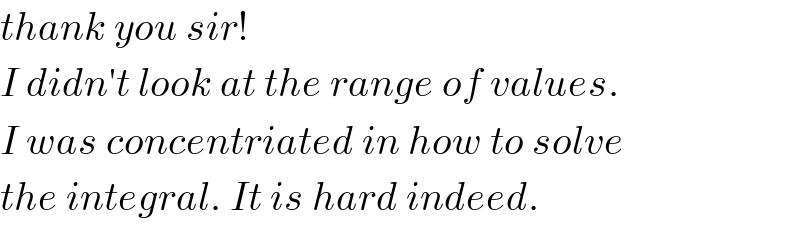
$${thank}\:{you}\:{sir}! \\ $$$${I}\:{didn}'{t}\:{look}\:{at}\:{the}\:{range}\:{of}\:{values}. \\ $$$${I}\:{was}\:{concentriated}\:{in}\:{how}\:{to}\:{solve} \\ $$$${the}\:{integral}.\:{It}\:{is}\:{hard}\:{indeed}. \\ $$
Commented by mrW2 last updated on 27/Feb/18
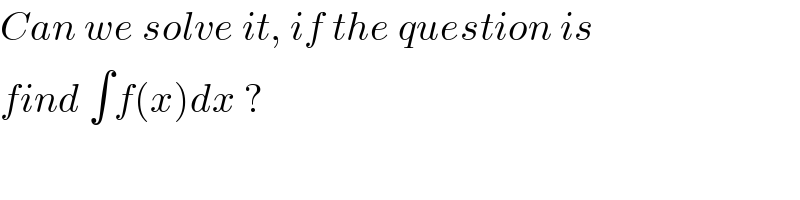
$${Can}\:{we}\:{solve}\:{it},\:{if}\:{the}\:{question}\:{is} \\ $$$${find}\:\int{f}\left({x}\right){dx}\:? \\ $$
Commented by prof Abdo imad last updated on 28/Feb/18
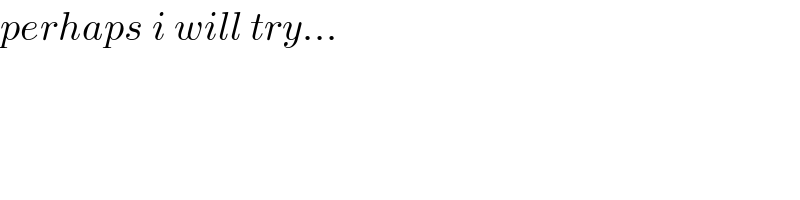
$${perhaps}\:{i}\:{will}\:{try}… \\ $$
Commented by ajfour last updated on 28/Feb/18

$${Thank}\:{you}\:{Sir}. \\ $$
Commented by abdo imad last updated on 28/Feb/18
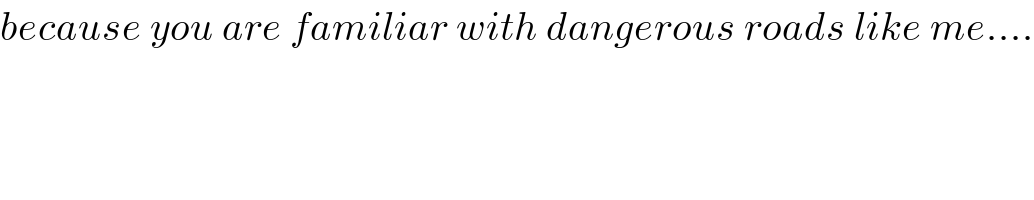
$${because}\:{you}\:{are}\:{familiar}\:{with}\:{dangerous}\:{roads}\:{like}\:{me}…. \\ $$
