Question Number 180826 by mnjuly1970 last updated on 17/Nov/22
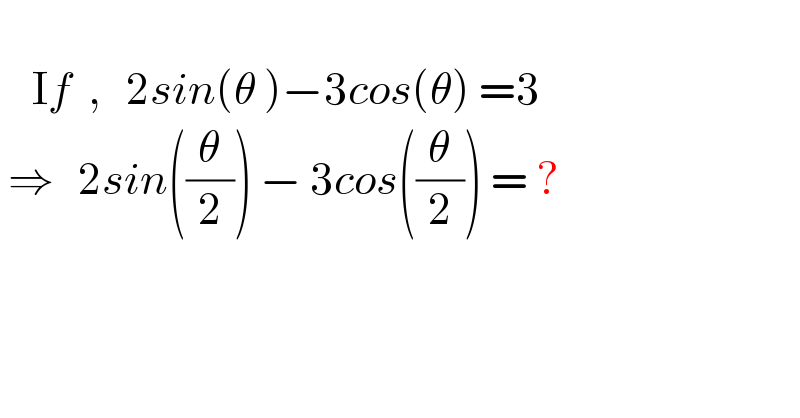
$$ \\ $$$$\:\:\:\:\mathrm{I}{f}\:\:,\:\:\:\mathrm{2}{sin}\left(\theta\:\right)−\mathrm{3}{cos}\left(\theta\right)\:=\mathrm{3} \\ $$$$\:\Rightarrow\:\:\:\mathrm{2}{sin}\left(\frac{\theta}{\mathrm{2}}\right)\:−\:\mathrm{3}{cos}\left(\frac{\theta}{\mathrm{2}}\right)\:=\:? \\ $$$$ \\ $$
Answered by mr W last updated on 17/Nov/22
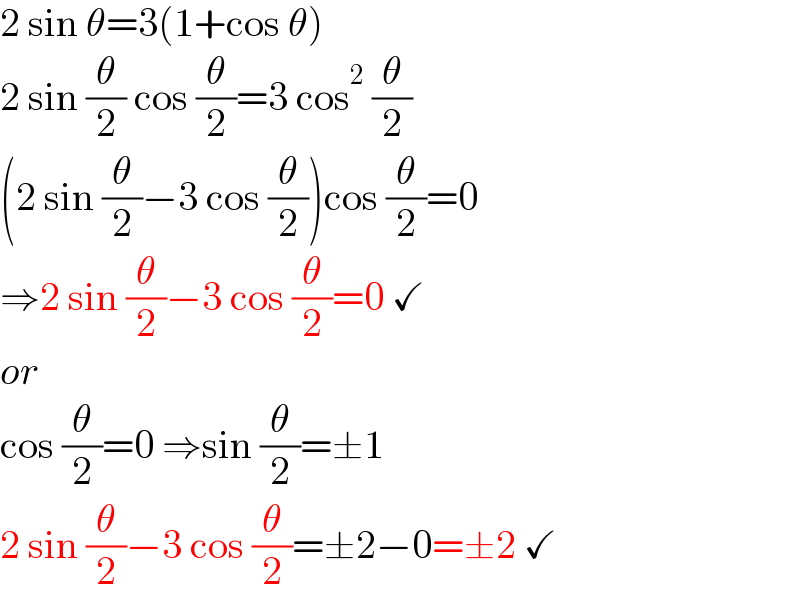
$$\mathrm{2}\:\mathrm{sin}\:\theta=\mathrm{3}\left(\mathrm{1}+\mathrm{cos}\:\theta\right) \\ $$$$\mathrm{2}\:\mathrm{sin}\:\frac{\theta}{\mathrm{2}}\:\mathrm{cos}\:\frac{\theta}{\mathrm{2}}=\mathrm{3}\:\mathrm{cos}^{\mathrm{2}} \:\frac{\theta}{\mathrm{2}} \\ $$$$\left(\mathrm{2}\:\mathrm{sin}\:\frac{\theta}{\mathrm{2}}−\mathrm{3}\:\mathrm{cos}\:\frac{\theta}{\mathrm{2}}\right)\mathrm{cos}\:\frac{\theta}{\mathrm{2}}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{2}\:\mathrm{sin}\:\frac{\theta}{\mathrm{2}}−\mathrm{3}\:\mathrm{cos}\:\frac{\theta}{\mathrm{2}}=\mathrm{0}\:\checkmark \\ $$$${or} \\ $$$$\mathrm{cos}\:\frac{\theta}{\mathrm{2}}=\mathrm{0}\:\Rightarrow\mathrm{sin}\:\frac{\theta}{\mathrm{2}}=\pm\mathrm{1} \\ $$$$\mathrm{2}\:\mathrm{sin}\:\frac{\theta}{\mathrm{2}}−\mathrm{3}\:\mathrm{cos}\:\frac{\theta}{\mathrm{2}}=\pm\mathrm{2}−\mathrm{0}=\pm\mathrm{2}\:\checkmark \\ $$
