Question Number 92424 by Jidda28 last updated on 06/May/20
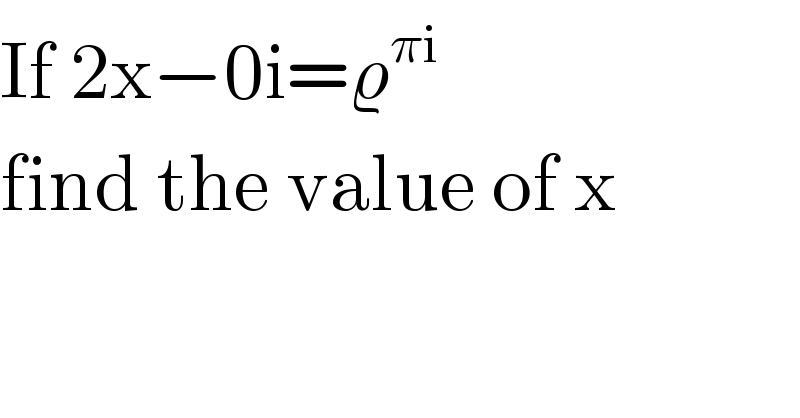
$$\mathrm{If}\:\mathrm{2x}−\mathrm{0i}=\varrho^{\pi\mathrm{i}} \: \\ $$$$\mathrm{find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{x} \\ $$
Commented by mathmax by abdo last updated on 06/May/20
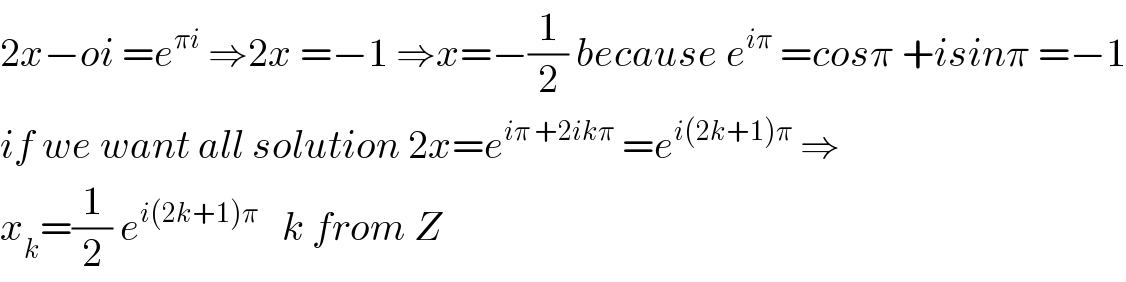
$$\mathrm{2}{x}−{oi}\:={e}^{\pi{i}} \:\Rightarrow\mathrm{2}{x}\:=−\mathrm{1}\:\Rightarrow{x}=−\frac{\mathrm{1}}{\mathrm{2}}\:{because}\:{e}^{{i}\pi} \:={cos}\pi\:+{isin}\pi\:=−\mathrm{1} \\ $$$${if}\:{we}\:{want}\:{all}\:{solution}\:\mathrm{2}{x}={e}^{{i}\pi\:+\mathrm{2}{ik}\pi} \:={e}^{{i}\left(\mathrm{2}{k}+\mathrm{1}\right)\pi} \:\Rightarrow \\ $$$${x}_{{k}} =\frac{\mathrm{1}}{\mathrm{2}}\:{e}^{{i}\left(\mathrm{2}{k}+\mathrm{1}\right)\pi} \:\:\:{k}\:{from}\:{Z} \\ $$
Commented by Jidda28 last updated on 06/May/20
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{so}\:\mathrm{much}\:\mathrm{sir} \\ $$
Commented by mathmax by abdo last updated on 07/May/20
$${you}\:{are}\:{welcome}. \\ $$
