Question Number 148027 by mathdanisur last updated on 25/Jul/21
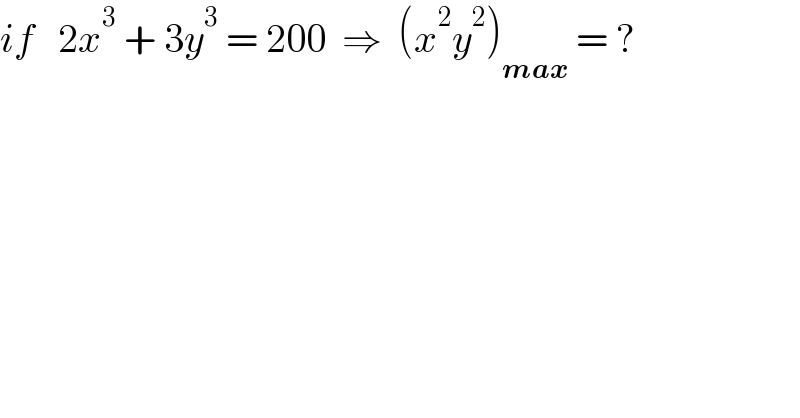
$${if}\:\:\:\mathrm{2}{x}^{\mathrm{3}} \:+\:\mathrm{3}{y}^{\mathrm{3}} \:=\:\mathrm{200}\:\:\Rightarrow\:\:\left({x}^{\mathrm{2}} {y}^{\mathrm{2}} \right)_{\boldsymbol{{max}}} \:=\:? \\ $$
Commented by mr W last updated on 25/Jul/21
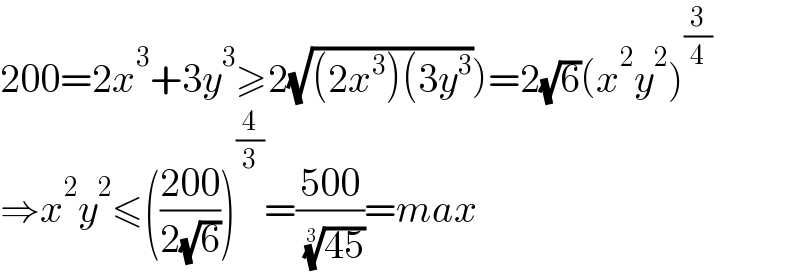
$$\left.\mathrm{200}=\mathrm{2}{x}^{\mathrm{3}} +\mathrm{3}{y}^{\mathrm{3}} \geqslant\mathrm{2}\sqrt{\left(\mathrm{2}{x}^{\mathrm{3}} \right)\left(\mathrm{3}{y}^{\mathrm{3}} \right.}\right)=\mathrm{2}\sqrt{\mathrm{6}}\left({x}^{\mathrm{2}} {y}^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{4}}} \\ $$$$\Rightarrow{x}^{\mathrm{2}} {y}^{\mathrm{2}} \leqslant\left(\frac{\mathrm{200}}{\mathrm{2}\sqrt{\mathrm{6}}}\right)^{\frac{\mathrm{4}}{\mathrm{3}}} =\frac{\mathrm{500}}{\:\sqrt[{\mathrm{3}}]{\mathrm{45}}}={max} \\ $$
Commented by mathdanisur last updated on 25/Jul/21

$${Thank}\:{you}\:{Sir} \\ $$
Commented by mathdanisur last updated on 25/Jul/21
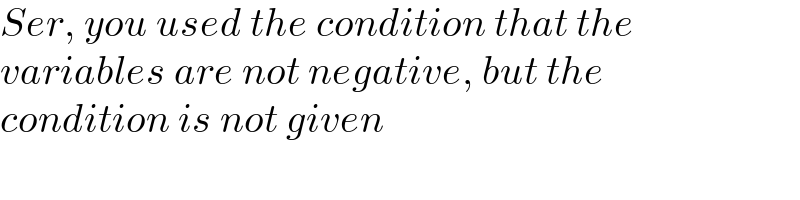
$${Ser},\:{you}\:{used}\:{the}\:{condition}\:{that}\:{the} \\ $$$${variables}\:{are}\:{not}\:{negative},\:{but}\:{the} \\ $$$${condition}\:{is}\:{not}\:{given} \\ $$
Commented by mr W last updated on 25/Jul/21

$${for}\:{local}\:{maximum},\:{both}\:{x}\:{and}\:{y}\:{are} \\ $$$${positive}. \\ $$$${in}\:{fact}\:{this}\:{question}\:{is}\:{not}\:{a}\:{good}\:{one}, \\ $$$${since}\:\left({x}^{\mathrm{2}} {y}^{\mathrm{2}} \right)\:{has}\:{neither}\:{a}\:{maximum} \\ $$$${nor}\:{a}\:{minimum}. \\ $$
Answered by Olaf_Thorendsen last updated on 25/Jul/21
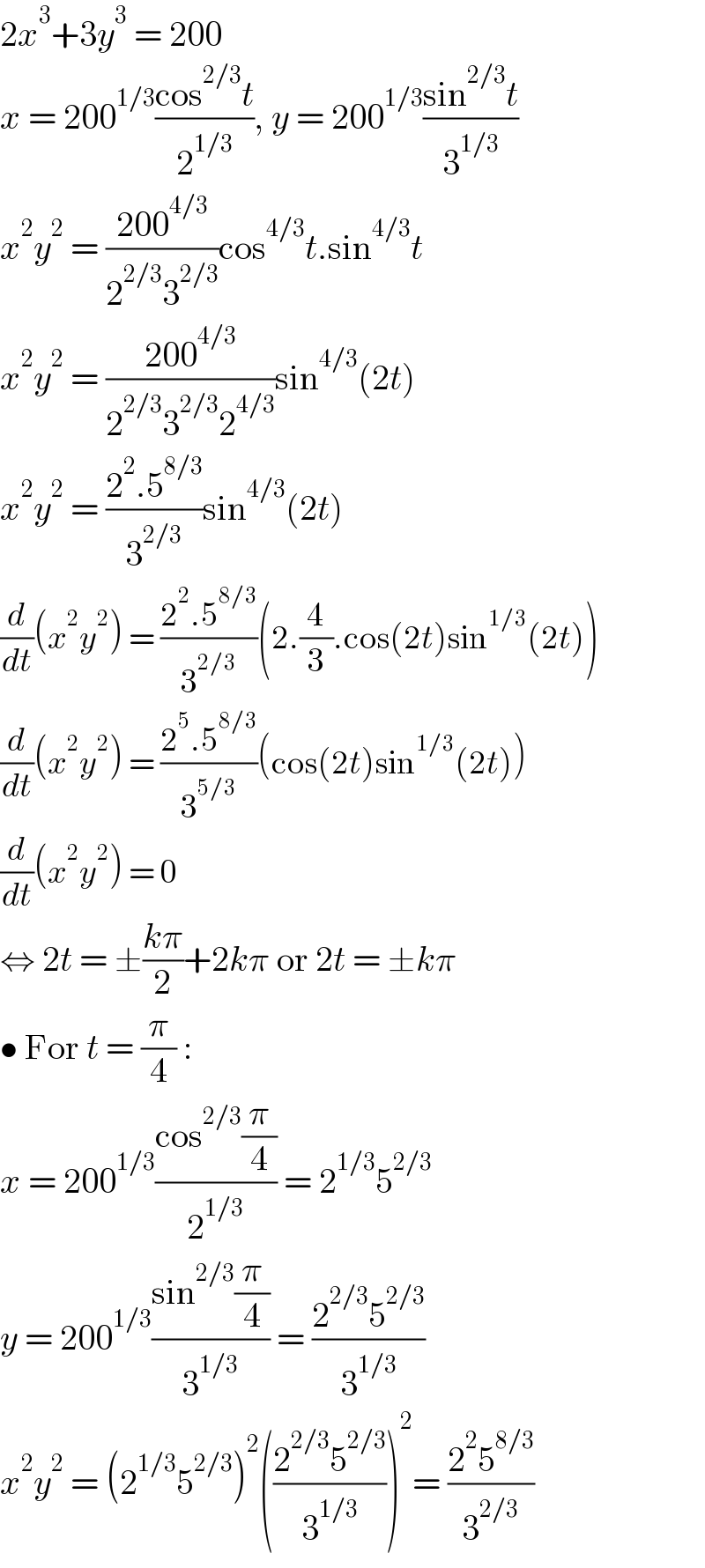
$$\mathrm{2}{x}^{\mathrm{3}} +\mathrm{3}{y}^{\mathrm{3}} \:=\:\mathrm{200} \\ $$$${x}\:=\:\mathrm{200}^{\mathrm{1}/\mathrm{3}} \frac{\mathrm{cos}^{\mathrm{2}/\mathrm{3}} {t}}{\mathrm{2}^{\mathrm{1}/\mathrm{3}} },\:{y}\:=\:\mathrm{200}^{\mathrm{1}/\mathrm{3}} \frac{\mathrm{sin}^{\mathrm{2}/\mathrm{3}} {t}}{\mathrm{3}^{\mathrm{1}/\mathrm{3}} } \\ $$$${x}^{\mathrm{2}} {y}^{\mathrm{2}} \:=\:\frac{\mathrm{200}^{\mathrm{4}/\mathrm{3}} }{\mathrm{2}^{\mathrm{2}/\mathrm{3}} \mathrm{3}^{\mathrm{2}/\mathrm{3}} }\mathrm{cos}^{\mathrm{4}/\mathrm{3}} {t}.\mathrm{sin}^{\mathrm{4}/\mathrm{3}} {t} \\ $$$${x}^{\mathrm{2}} {y}^{\mathrm{2}} \:=\:\frac{\mathrm{200}^{\mathrm{4}/\mathrm{3}} }{\mathrm{2}^{\mathrm{2}/\mathrm{3}} \mathrm{3}^{\mathrm{2}/\mathrm{3}} \mathrm{2}^{\mathrm{4}/\mathrm{3}} }\mathrm{sin}^{\mathrm{4}/\mathrm{3}} \left(\mathrm{2}{t}\right) \\ $$$${x}^{\mathrm{2}} {y}^{\mathrm{2}} \:=\:\frac{\mathrm{2}^{\mathrm{2}} .\mathrm{5}^{\mathrm{8}/\mathrm{3}} }{\mathrm{3}^{\mathrm{2}/\mathrm{3}} }\mathrm{sin}^{\mathrm{4}/\mathrm{3}} \left(\mathrm{2}{t}\right) \\ $$$$\frac{{d}}{{dt}}\left({x}^{\mathrm{2}} {y}^{\mathrm{2}} \right)\:=\:\frac{\mathrm{2}^{\mathrm{2}} .\mathrm{5}^{\mathrm{8}/\mathrm{3}} }{\mathrm{3}^{\mathrm{2}/\mathrm{3}} }\left(\mathrm{2}.\frac{\mathrm{4}}{\mathrm{3}}.\mathrm{cos}\left(\mathrm{2}{t}\right)\mathrm{sin}^{\mathrm{1}/\mathrm{3}} \left(\mathrm{2}{t}\right)\right) \\ $$$$\frac{{d}}{{dt}}\left({x}^{\mathrm{2}} {y}^{\mathrm{2}} \right)\:=\:\frac{\mathrm{2}^{\mathrm{5}} .\mathrm{5}^{\mathrm{8}/\mathrm{3}} }{\mathrm{3}^{\mathrm{5}/\mathrm{3}} }\left(\mathrm{cos}\left(\mathrm{2}{t}\right)\mathrm{sin}^{\mathrm{1}/\mathrm{3}} \left(\mathrm{2}{t}\right)\right) \\ $$$$\frac{{d}}{{dt}}\left({x}^{\mathrm{2}} {y}^{\mathrm{2}} \right)\:=\:\mathrm{0} \\ $$$$\Leftrightarrow\:\mathrm{2}{t}\:=\:\pm\frac{{k}\pi}{\mathrm{2}}+\mathrm{2}{k}\pi\:\mathrm{or}\:\mathrm{2}{t}\:=\:\pm{k}\pi \\ $$$$\bullet\:\mathrm{For}\:{t}\:=\:\frac{\pi}{\mathrm{4}}\:: \\ $$$${x}\:=\:\mathrm{200}^{\mathrm{1}/\mathrm{3}} \frac{\mathrm{cos}^{\mathrm{2}/\mathrm{3}} \frac{\pi}{\mathrm{4}}}{\mathrm{2}^{\mathrm{1}/\mathrm{3}} }\:=\:\mathrm{2}^{\mathrm{1}/\mathrm{3}} \mathrm{5}^{\mathrm{2}/\mathrm{3}} \\ $$$${y}\:=\:\mathrm{200}^{\mathrm{1}/\mathrm{3}} \frac{\mathrm{sin}^{\mathrm{2}/\mathrm{3}} \frac{\pi}{\mathrm{4}}}{\mathrm{3}^{\mathrm{1}/\mathrm{3}} }\:=\:\frac{\mathrm{2}^{\mathrm{2}/\mathrm{3}} \mathrm{5}^{\mathrm{2}/\mathrm{3}} }{\mathrm{3}^{\mathrm{1}/\mathrm{3}} } \\ $$$${x}^{\mathrm{2}} {y}^{\mathrm{2}} \:=\:\left(\mathrm{2}^{\mathrm{1}/\mathrm{3}} \mathrm{5}^{\mathrm{2}/\mathrm{3}} \right)^{\mathrm{2}} \left(\frac{\mathrm{2}^{\mathrm{2}/\mathrm{3}} \mathrm{5}^{\mathrm{2}/\mathrm{3}} }{\mathrm{3}^{\mathrm{1}/\mathrm{3}} }\right)^{\mathrm{2}} =\:\frac{\mathrm{2}^{\mathrm{2}} \mathrm{5}^{\mathrm{8}/\mathrm{3}} }{\mathrm{3}^{\mathrm{2}/\mathrm{3}} } \\ $$
Commented by mr W last updated on 25/Jul/21

$${please}\:{check}\:{before}\:{saying}! \\ $$$${but}\:\mathrm{50}\left(\mathrm{25}^{\frac{\mathrm{1}}{\mathrm{3}}} \right)\:{is}\:{wrong}! \\ $$$${and}\:\frac{\mathrm{2}^{\mathrm{2}} \mathrm{5}^{\mathrm{8}/\mathrm{3}} }{\mathrm{3}^{\mathrm{2}/\mathrm{3}} }\:{is}\:{right}! \\ $$
Commented by mathdanisur last updated on 25/Jul/21
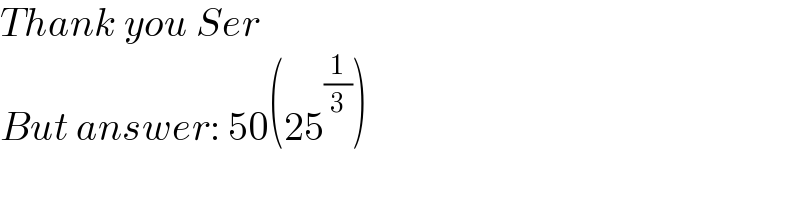
$${Thank}\:{you}\:{Ser} \\ $$$${But}\:{answer}:\:\mathrm{50}\left(\mathrm{25}^{\frac{\mathrm{1}}{\mathrm{3}}} \right) \\ $$
Commented by mathdanisur last updated on 25/Jul/21

$${Thankyou}\:{Ser} \\ $$
