Question Number 147432 by mathdanisur last updated on 20/Jul/21
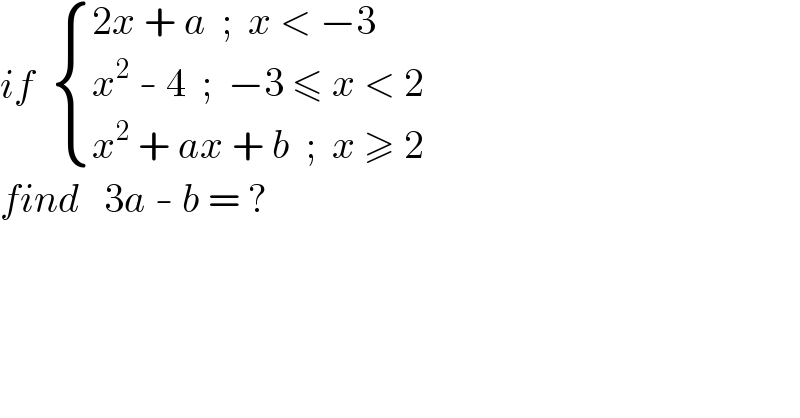
$${if}\:\:\begin{cases}{\mathrm{2}{x}\:+\:{a}\:\:;\:\:{x}\:<\:−\mathrm{3}}\\{{x}^{\mathrm{2}} \:-\:\mathrm{4}\:\:;\:\:−\mathrm{3}\:\leqslant\:{x}\:<\:\mathrm{2}}\\{{x}^{\mathrm{2}} \:+\:{ax}\:+\:{b}\:\:;\:\:{x}\:\geqslant\:\mathrm{2}}\end{cases} \\ $$$${find}\:\:\:\mathrm{3}{a}\:-\:{b}\:=\:? \\ $$
Answered by liberty last updated on 21/Jul/21
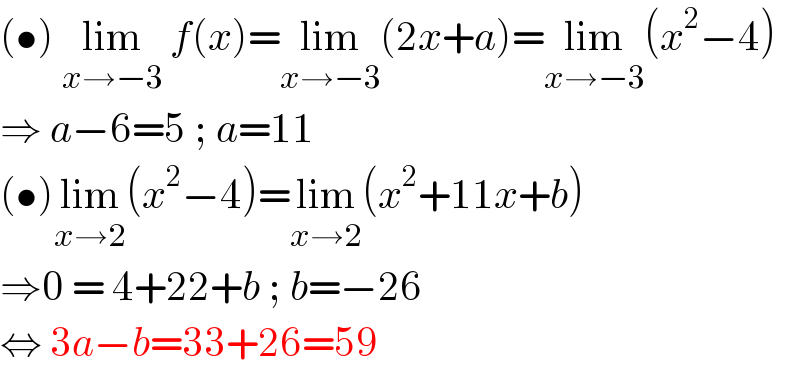
$$\left(\bullet\right)\:\underset{{x}\rightarrow−\mathrm{3}} {\mathrm{lim}}\:{f}\left({x}\right)=\underset{{x}\rightarrow−\mathrm{3}} {\mathrm{lim}}\left(\mathrm{2}{x}+{a}\right)=\underset{{x}\rightarrow−\mathrm{3}} {\mathrm{lim}}\left({x}^{\mathrm{2}} −\mathrm{4}\right) \\ $$$$\Rightarrow\:{a}−\mathrm{6}=\mathrm{5}\:;\:{a}=\mathrm{11} \\ $$$$\left(\bullet\right)\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\left({x}^{\mathrm{2}} −\mathrm{4}\right)=\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\left({x}^{\mathrm{2}} +\mathrm{11}{x}+{b}\right) \\ $$$$\Rightarrow\mathrm{0}\:=\:\mathrm{4}+\mathrm{22}+{b}\:;\:{b}=−\mathrm{26} \\ $$$$\Leftrightarrow\:\mathrm{3}{a}−{b}=\mathrm{33}+\mathrm{26}=\mathrm{59} \\ $$
Commented by mathdanisur last updated on 21/Jul/21

$${thank}\:{you}\:{Sir} \\ $$
