If-2z-1-3z-2-is-a-purely-imaginary-number-then-find-the-value-of-z-1-z-2-z-1-z-2-

Question Number 32028 by rahul 19 last updated on 18/Mar/18

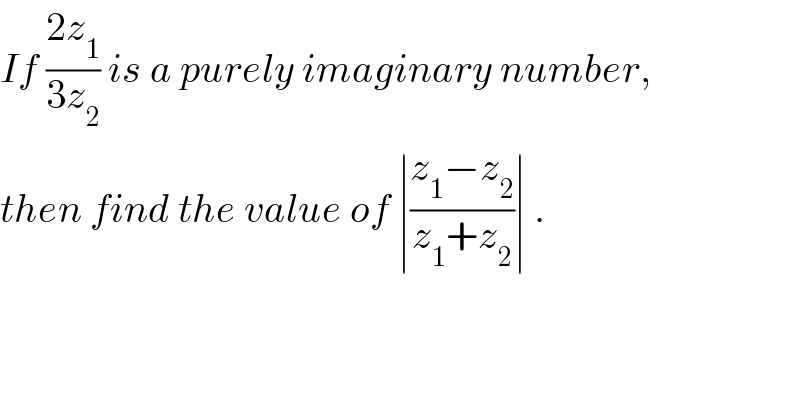
$${If}\:\frac{\mathrm{2}{z}_{\mathrm{1}} }{\mathrm{3}{z}_{\mathrm{2}} }\:{is}\:{a}\:{purely}\:{imaginary}\:{number}, \\ $$$${then}\:{find}\:{the}\:{value}\:{of}\:\mid\frac{{z}_{\mathrm{1}} −{z}_{\mathrm{2}} }{{z}_{\mathrm{1}} +{z}_{\mathrm{2}} }\mid\:. \\ $$

Answered by Giannibo last updated on 18/Mar/18

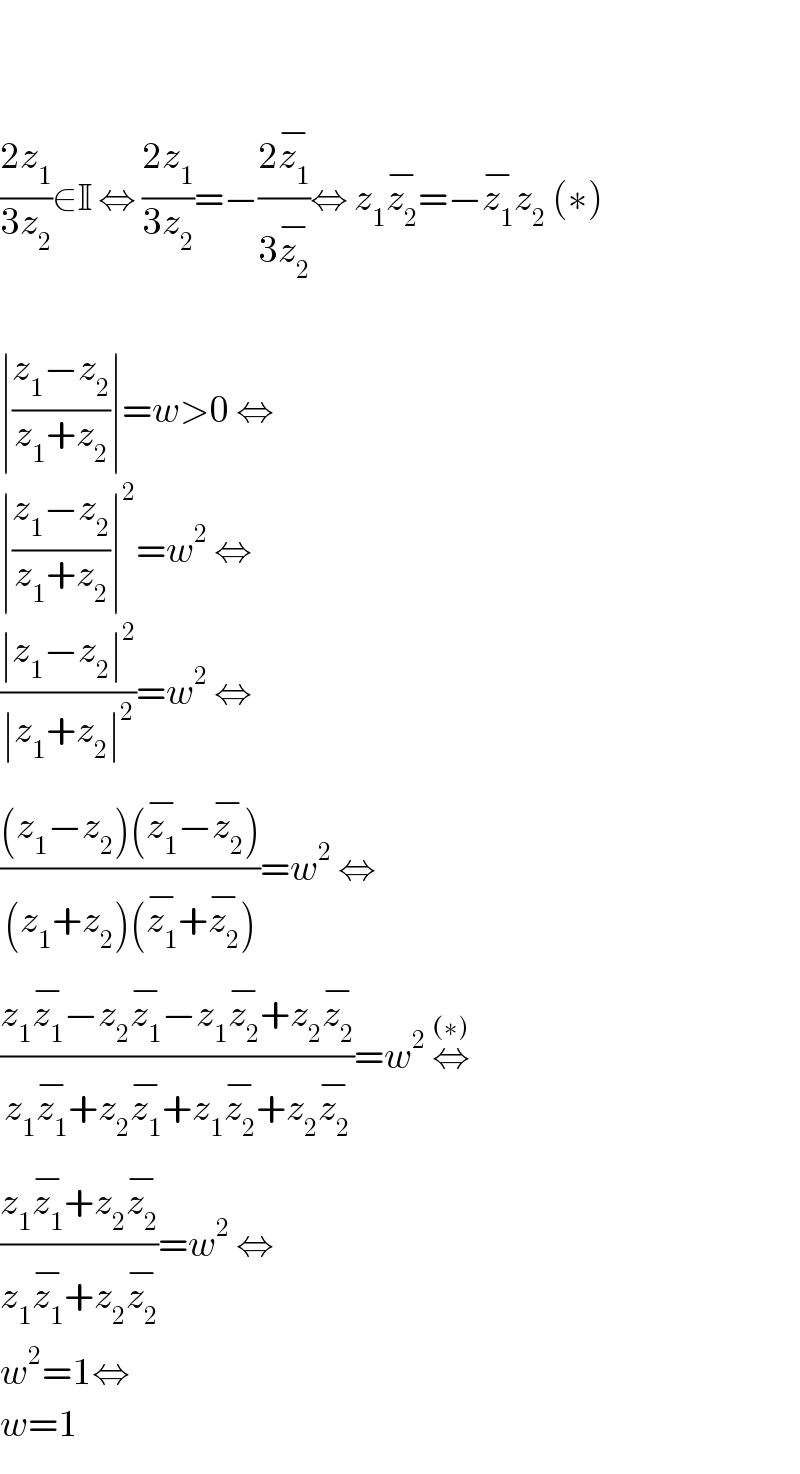
$$ \\ $$$$ \\ $$$$\frac{\mathrm{2}{z}_{\mathrm{1}} }{\mathrm{3}{z}_{\mathrm{2}} }\in\mathbb{I}\:\Leftrightarrow\:\frac{\mathrm{2}{z}_{\mathrm{1}} }{\mathrm{3}{z}_{\mathrm{2}} }=−\frac{\mathrm{2}\overline {{z}_{\mathrm{1}} }}{\mathrm{3}\overline {{z}_{\mathrm{2}} }}\Leftrightarrow\:{z}_{\mathrm{1}} \overline {{z}_{\mathrm{2}} }=−\overline {{z}_{\mathrm{1}} }{z}_{\mathrm{2}} \:\left(\ast\right) \\ $$$$ \\ $$$$\mid\frac{{z}_{\mathrm{1}} −{z}_{\mathrm{2}} }{{z}_{\mathrm{1}} +{z}_{\mathrm{2}} }\mid={w}>\mathrm{0}\:\Leftrightarrow \\ $$$$\mid\frac{{z}_{\mathrm{1}} −{z}_{\mathrm{2}} }{{z}_{\mathrm{1}} +{z}_{\mathrm{2}} }\mid^{\mathrm{2}} ={w}^{\mathrm{2}} \:\Leftrightarrow \\ $$$$\frac{\mid{z}_{\mathrm{1}} −{z}_{\mathrm{2}} \mid^{\mathrm{2}} }{\mid{z}_{\mathrm{1}} +{z}_{\mathrm{2}} \mid^{\mathrm{2}} }={w}^{\mathrm{2}} \:\Leftrightarrow \\ $$$$\frac{\left({z}_{\mathrm{1}} −{z}_{\mathrm{2}} \right)\left(\overline {{z}_{\mathrm{1}} }−\overline {{z}_{\mathrm{2}} }\right)}{\left({z}_{\mathrm{1}} +{z}_{\mathrm{2}} \right)\left(\overline {{z}_{\mathrm{1}} }+\overline {{z}_{\mathrm{2}} }\right)}={w}^{\mathrm{2}} \:\Leftrightarrow \\ $$$$\frac{{z}_{\mathrm{1}} \overline {{z}_{\mathrm{1}} }−{z}_{\mathrm{2}} \overline {{z}_{\mathrm{1}} }−{z}_{\mathrm{1}} \overline {{z}_{\mathrm{2}} }+{z}_{\mathrm{2}} \overline {{z}_{\mathrm{2}} }}{{z}_{\mathrm{1}} \overline {{z}_{\mathrm{1}} }+{z}_{\mathrm{2}} \overline {{z}_{\mathrm{1}} }+{z}_{\mathrm{1}} \overline {{z}_{\mathrm{2}} }+{z}_{\mathrm{2}} \overline {{z}_{\mathrm{2}} }}={w}^{\mathrm{2}} \:\overset{\left(\ast\right)} {\Leftrightarrow} \\ $$$$\frac{{z}_{\mathrm{1}} \overline {{z}_{\mathrm{1}} }+{z}_{\mathrm{2}} \overline {{z}_{\mathrm{2}} }}{{z}_{\mathrm{1}} \overline {{z}_{\mathrm{1}} }+{z}_{\mathrm{2}} \overline {{z}_{\mathrm{2}} }}={w}^{\mathrm{2}} \:\Leftrightarrow \\ $$$${w}^{\mathrm{2}} =\mathrm{1}\Leftrightarrow \\ $$$${w}=\mathrm{1} \\ $$

Commented by rahul 19 last updated on 18/Mar/18

$${thank}\:{u}\:{sir}! \\ $$

Terms of Service
Privacy Policy
Contact: info@tinkutara.com