Question Number 146467 by mathdanisur last updated on 13/Jul/21
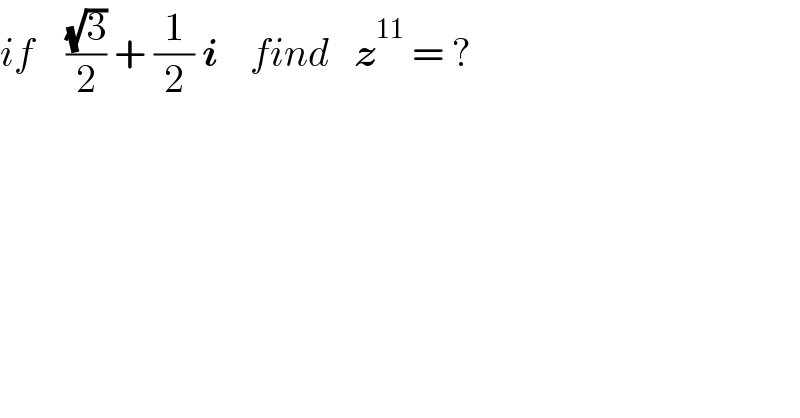
$${if}\:\:\:\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:+\:\frac{\mathrm{1}}{\mathrm{2}}\:\boldsymbol{{i}}\:\:\:\:{find}\:\:\:\boldsymbol{{z}}^{\mathrm{11}} \:=\:? \\ $$
Answered by gsk2684 last updated on 13/Jul/21

$${z}^{\mathrm{11}} \:=\:\left({cis}\:\frac{\Pi}{\mathrm{6}}\right)^{\mathrm{11}} =\:{cis}\left(\frac{\mathrm{11}\Pi}{\mathrm{6}}\right) \\ $$$$={cis}\left(\mathrm{2}\Pi−\frac{\Pi}{\mathrm{6}}\right) \\ $$$$={cis}\left(−\frac{\Pi}{\mathrm{6}}\right) \\ $$$$=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}−\frac{{i}}{\mathrm{2}} \\ $$
Commented by mathdanisur last updated on 13/Jul/21
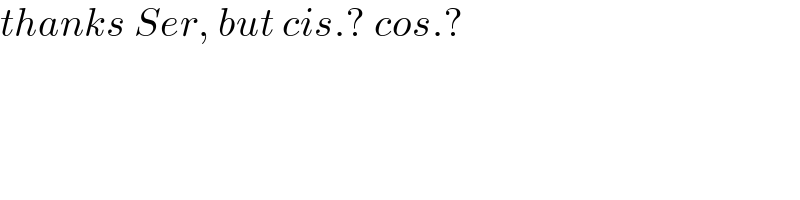
$${thanks}\:{Ser},\:{but}\:{cis}.?\:{cos}.? \\ $$
Commented by gsk2684 last updated on 13/Jul/21

$${cis}\:\theta\:=\:\mathrm{cos}\:\theta\:+\:{i}\:\mathrm{sin}\:\theta \\ $$
Commented by mathdanisur last updated on 13/Jul/21

$${thanks}\:{Ser} \\ $$
Answered by puissant last updated on 13/Jul/21

$$\mathrm{Z}=\mathrm{cos}\frac{\pi}{\mathrm{6}}+\mathrm{i}\:\mathrm{sin}\frac{\pi}{\mathrm{6}}=\mathrm{e}^{\mathrm{i}\frac{\pi}{\mathrm{6}}} \\ $$$$\mathrm{Z}^{\mathrm{11}} =\left(\mathrm{e}^{\mathrm{i}\frac{\pi}{\mathrm{6}}} \right)^{\mathrm{11}} =\mathrm{e}^{\mathrm{i}\frac{\mathrm{11}\pi}{\mathrm{6}}} =\:\mathrm{cos}\frac{\mathrm{11}\pi}{\mathrm{6}}+\mathrm{i}\:\mathrm{sin}\frac{\mathrm{11}\pi}{\mathrm{6}} \\ $$$$\Rightarrow\:\mathrm{Z}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{i} \\ $$
Commented by mathdanisur last updated on 13/Jul/21

$${thank}\:{you}\:{Ser} \\ $$$${cos}\frac{\mathrm{11}\pi}{\mathrm{6}}+{isin}\frac{\mathrm{11}\pi}{\mathrm{6}}\Rightarrow{z}^{\mathrm{11}} =\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}{i}.? \\ $$
Commented by mathdanisur last updated on 13/Jul/21

$${thanks}\:{Ser} \\ $$
