Menu Close

If-3sin-x-4cos-x-5-then-sin-x-

Tinku Tara 0 Comments
Pin




Question Number 100131 by bemath last updated on 25/Jun/20
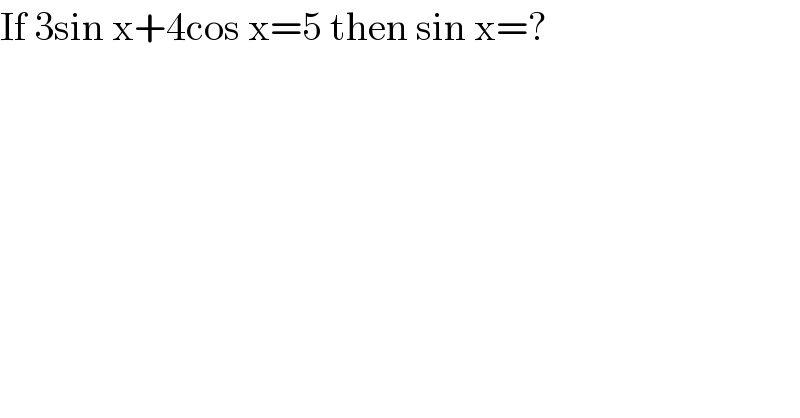
If 3sin x+4cos x=5 then sin x=?
$$\mathrm{If}\:\mathrm{3sin}\:\mathrm{x}+\mathrm{4cos}\:\mathrm{x}=\mathrm{5}\:\mathrm{then}\:\mathrm{sin}\:\mathrm{x}=? \\ $$
Commented by bobhans last updated on 25/Jun/20
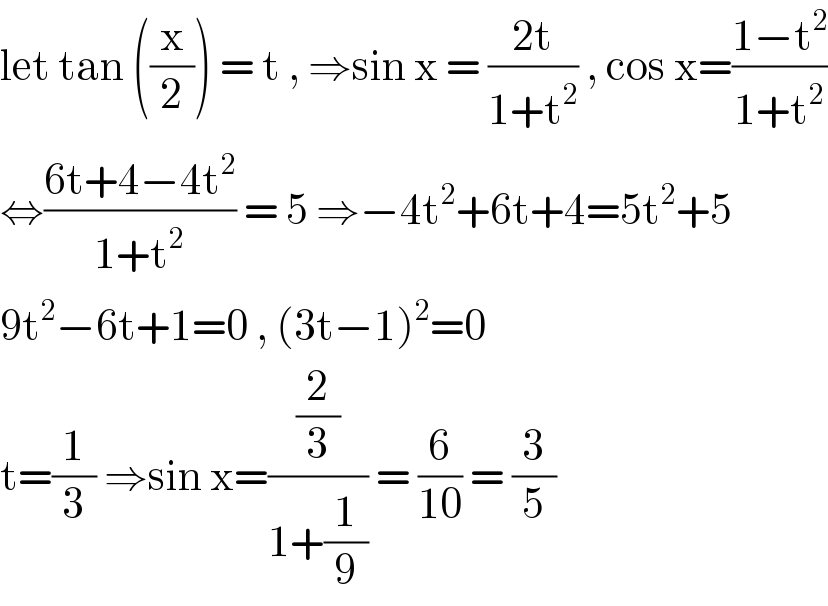
let tan ((x/2)) = t , ⇒sin x = ((2t)/(1+t^2 )) , cos x=((1−t^2 )/(1+t^2 )) ⇔((6t+4−4t^2 )/(1+t^2 )) = 5 ⇒−4t^2 +6t+4=5t^2 +5 9t^2 −6t+1=0 , (3t−1)^2 =0 t=(1/3) ⇒sin x=((2/3)/(1+(1/9))) = (6/(10)) = (3/5)
$$\mathrm{let}\:\mathrm{tan}\:\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\:=\:\mathrm{t}\:,\:\Rightarrow\mathrm{sin}\:\mathrm{x}\:=\:\frac{\mathrm{2t}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\:,\:\mathrm{cos}\:\mathrm{x}=\frac{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }{\mathrm{1}+\mathrm{t}^{\mathrm{2}} } \\ $$$$\Leftrightarrow\frac{\mathrm{6t}+\mathrm{4}−\mathrm{4t}^{\mathrm{2}} }{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\:=\:\mathrm{5}\:\Rightarrow−\mathrm{4t}^{\mathrm{2}} +\mathrm{6t}+\mathrm{4}=\mathrm{5t}^{\mathrm{2}} +\mathrm{5} \\ $$$$\mathrm{9t}^{\mathrm{2}} −\mathrm{6t}+\mathrm{1}=\mathrm{0}\:,\:\left(\mathrm{3t}−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{t}=\frac{\mathrm{1}}{\mathrm{3}}\:\Rightarrow\mathrm{sin}\:\mathrm{x}=\frac{\frac{\mathrm{2}}{\mathrm{3}}}{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{9}}}\:=\:\frac{\mathrm{6}}{\mathrm{10}}\:=\:\frac{\mathrm{3}}{\mathrm{5}} \\ $$
Commented by bemath last updated on 25/Jun/20
thank you all
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{all}\: \\ $$
Commented by Dwaipayan Shikari last updated on 25/Jun/20
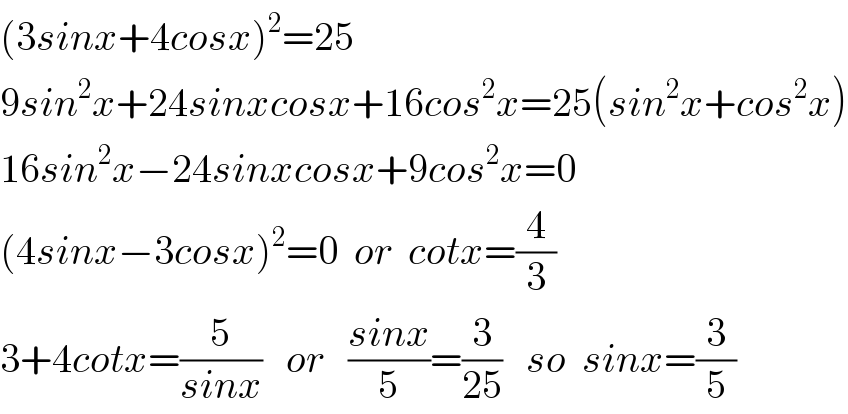
(3sinx+4cosx)^2 =25 9sin^2 x+24sinxcosx+16cos^2 x=25(sin^2 x+cos^2 x) 16sin^2 x−24sinxcosx+9cos^2 x=0 (4sinx−3cosx)^2 =0 or cotx=(4/3) 3+4cotx=(5/(sinx)) or ((sinx)/5)=(3/(25)) so sinx=(3/5)
$$\left(\mathrm{3}{sinx}+\mathrm{4}{cosx}\right)^{\mathrm{2}} =\mathrm{25} \\ $$$$\mathrm{9}{sin}^{\mathrm{2}} {x}+\mathrm{24}{sinxcosx}+\mathrm{16}{cos}^{\mathrm{2}} {x}=\mathrm{25}\left({sin}^{\mathrm{2}} {x}+{cos}^{\mathrm{2}} {x}\right) \\ $$$$\mathrm{16}{sin}^{\mathrm{2}} {x}−\mathrm{24}{sinxcosx}+\mathrm{9}{cos}^{\mathrm{2}} {x}=\mathrm{0} \\ $$$$\left(\mathrm{4}{sinx}−\mathrm{3}{cosx}\right)^{\mathrm{2}} =\mathrm{0}\:\:{or}\:\:{cotx}=\frac{\mathrm{4}}{\mathrm{3}} \\ $$$$\mathrm{3}+\mathrm{4}{cotx}=\frac{\mathrm{5}}{{sinx}}\:\:\:{or}\:\:\:\frac{{sinx}}{\mathrm{5}}=\frac{\mathrm{3}}{\mathrm{25}}\:\:\:{so}\:\:{sinx}=\frac{\mathrm{3}}{\mathrm{5}} \\ $$
Answered by Rasheed.Sindhi last updated on 25/Jun/20
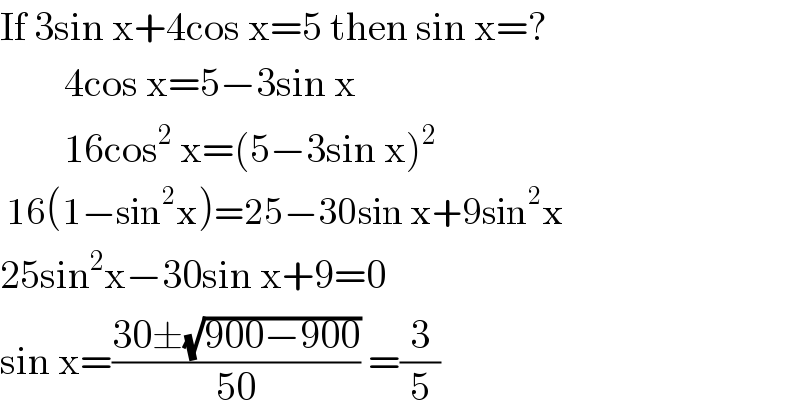
If 3sin x+4cos x=5 then sin x=? 4cos x=5−3sin x 16cos^2 x=(5−3sin x)^2 16(1−sin^2 x)=25−30sin x+9sin^2 x 25sin^2 x−30sin x+9=0 sin x=((30±(√(900−900)))/(50)) =(3/5)
$$\mathrm{If}\:\mathrm{3sin}\:\mathrm{x}+\mathrm{4cos}\:\mathrm{x}=\mathrm{5}\:\mathrm{then}\:\mathrm{sin}\:\mathrm{x}=? \\ $$$$\:\:\:\:\:\:\:\:\mathrm{4cos}\:\mathrm{x}=\mathrm{5}−\mathrm{3sin}\:\mathrm{x} \\ $$$$\:\:\:\:\:\:\:\:\mathrm{16cos}^{\mathrm{2}} \:\mathrm{x}=\left(\mathrm{5}−\mathrm{3sin}\:\mathrm{x}\right)^{\mathrm{2}} \\ $$$$\:\mathrm{16}\left(\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \mathrm{x}\right)=\mathrm{25}−\mathrm{30sin}\:\mathrm{x}+\mathrm{9sin}^{\mathrm{2}} \mathrm{x}\:\:\: \\ $$$$\mathrm{25sin}^{\mathrm{2}} \mathrm{x}−\mathrm{30sin}\:\mathrm{x}+\mathrm{9}=\mathrm{0}\: \\ $$$$\mathrm{sin}\:\mathrm{x}=\frac{\mathrm{30}\pm\sqrt{\mathrm{900}−\mathrm{900}}}{\mathrm{50}}\:=\frac{\mathrm{3}}{\mathrm{5}} \\ $$
Answered by mr W last updated on 25/Jun/20
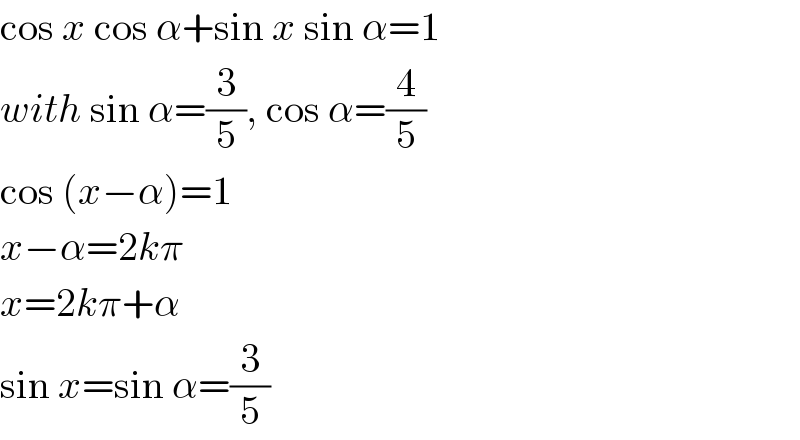
cos x cos α+sin x sin α=1 with sin α=(3/5), cos α=(4/5) cos (x−α)=1 x−α=2kπ x=2kπ+α sin x=sin α=(3/5)
$$\mathrm{cos}\:{x}\:\mathrm{cos}\:\alpha+\mathrm{sin}\:{x}\:\mathrm{sin}\:\alpha=\mathrm{1} \\ $$$${with}\:\mathrm{sin}\:\alpha=\frac{\mathrm{3}}{\mathrm{5}},\:\mathrm{cos}\:\alpha=\frac{\mathrm{4}}{\mathrm{5}} \\ $$$$\mathrm{cos}\:\left({x}−\alpha\right)=\mathrm{1} \\ $$$${x}−\alpha=\mathrm{2}{k}\pi \\ $$$${x}=\mathrm{2}{k}\pi+\alpha \\ $$$$\mathrm{sin}\:{x}=\mathrm{sin}\:\alpha=\frac{\mathrm{3}}{\mathrm{5}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *