If-3sin-x-4cos-y-3sin-y-8-then-sin-x-sin-y-

Question Number 173946 by mnjuly1970 last updated on 21/Jul/22

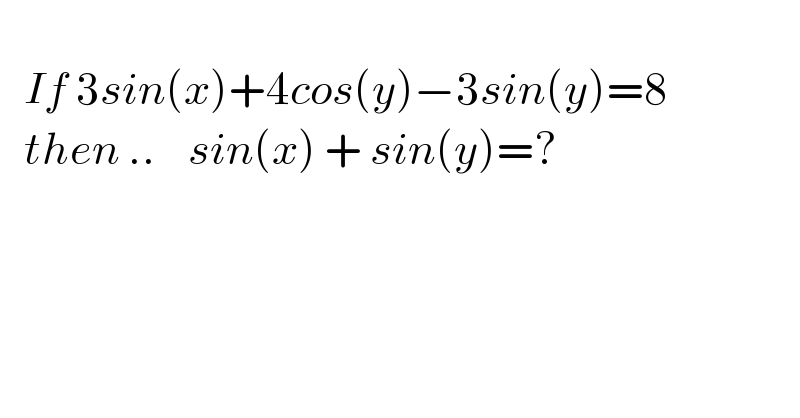
$$ \\ $$$$\:\:\:{If}\:\mathrm{3}{sin}\left({x}\right)+\mathrm{4}{cos}\left({y}\right)−\mathrm{3}{sin}\left({y}\right)=\mathrm{8} \\ $$$$\:\:\:{then}\:..\:\:\:\:{sin}\left({x}\right)\:+\:{sin}\left({y}\right)=? \\ $$$$ \\ $$$$ \\ $$

Answered by mr W last updated on 21/Jul/22

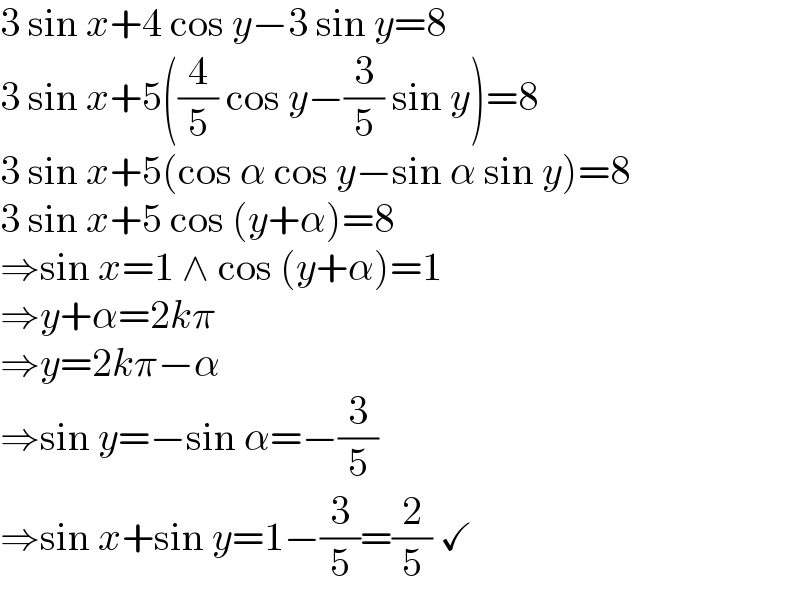
3 sin x+4 cos y−3 sin y=8 3 sin x+5((4/5) cos y−(3/5) sin y)=8 3 sin x+5(cos α cos y−sin α sin y)=8 3 sin x+5 cos (y+α)=8 ⇒sin x=1 ∧ cos (y+α)=1 ⇒y+α=2kπ ⇒y=2kπ−α ⇒sin y=−sin α=−(3/5) ⇒sin x+sin y=1−(3/5)=(2/5) ✓

$$\mathrm{3}\:\mathrm{sin}\:{x}+\mathrm{4}\:\mathrm{cos}\:{y}−\mathrm{3}\:\mathrm{sin}\:{y}=\mathrm{8} \\ $$$$\mathrm{3}\:\mathrm{sin}\:{x}+\mathrm{5}\left(\frac{\mathrm{4}}{\mathrm{5}}\:\mathrm{cos}\:{y}−\frac{\mathrm{3}}{\mathrm{5}}\:\mathrm{sin}\:{y}\right)=\mathrm{8} \\ $$$$\mathrm{3}\:\mathrm{sin}\:{x}+\mathrm{5}\left(\mathrm{cos}\:\alpha\:\mathrm{cos}\:{y}−\mathrm{sin}\:\alpha\:\mathrm{sin}\:{y}\right)=\mathrm{8} \\ $$$$\mathrm{3}\:\mathrm{sin}\:{x}+\mathrm{5}\:\mathrm{cos}\:\left({y}+\alpha\right)=\mathrm{8} \\ $$$$\Rightarrow\mathrm{sin}\:{x}=\mathrm{1}\:\wedge\:\mathrm{cos}\:\left({y}+\alpha\right)=\mathrm{1} \\ $$$$\Rightarrow{y}+\alpha=\mathrm{2}{k}\pi \\ $$$$\Rightarrow{y}=\mathrm{2}{k}\pi−\alpha \\ $$$$\Rightarrow\mathrm{sin}\:{y}=−\mathrm{sin}\:\alpha=−\frac{\mathrm{3}}{\mathrm{5}} \\ $$$$\Rightarrow\mathrm{sin}\:{x}+\mathrm{sin}\:{y}=\mathrm{1}−\frac{\mathrm{3}}{\mathrm{5}}=\frac{\mathrm{2}}{\mathrm{5}}\:\checkmark \\ $$

Commented by mathlove last updated on 22/Jul/22

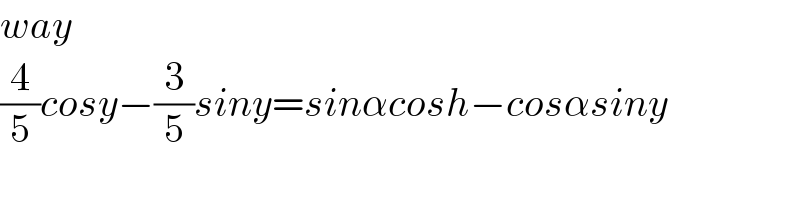
way (4/5)cosy−(3/5)siny=sinαcosh−cosαsiny

$${way} \\ $$$$\frac{\mathrm{4}}{\mathrm{5}}{cosy}−\frac{\mathrm{3}}{\mathrm{5}}{siny}={sin}\alpha{cosh}−{cos}\alpha{siny} \\ $$

Commented by infinityaction last updated on 22/Jul/22

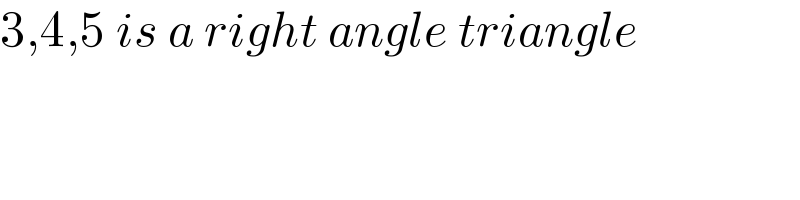
$$\mathrm{3},\mathrm{4},\mathrm{5}\:{is}\:{a}\:{right}\:{angle}\:{triangle} \\ $$

Commented by Tawa11 last updated on 22/Jul/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$

Commented by mr W last updated on 22/Jul/22

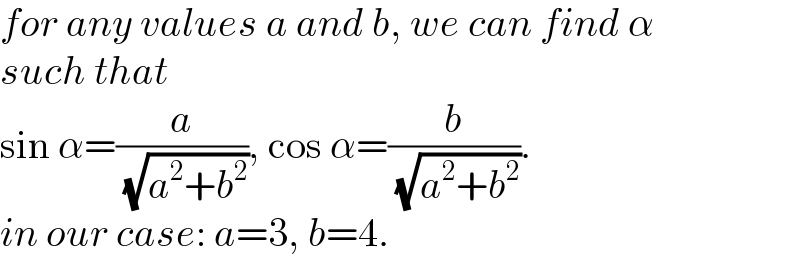
for any values a and b, we can find α such that sin α=(a/( (√(a^2 +b^2 )))), cos α=(b/( (√(a^2 +b^2 )))). in our case: a=3, b=4.

$${for}\:{any}\:{values}\:{a}\:{and}\:{b},\:{we}\:{can}\:{find}\:\alpha \\ $$$${such}\:{that} \\ $$$$\mathrm{sin}\:\alpha=\frac{{a}}{\:\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }},\:\mathrm{cos}\:\alpha=\frac{{b}}{\:\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }}. \\ $$$${in}\:{our}\:{case}:\:{a}=\mathrm{3},\:{b}=\mathrm{4}. \\ $$

Commented by mnjuly1970 last updated on 22/Jul/22

$${very}\:{nice}\:{sir}\:{W} \\ $$

Facebook Tweet Pin

If-3sin-x-4cos-y-3sin-y-8-then-sin-x-sin-y-

Leave a Reply Cancel reply