Question Number 119713 by som(math1967) last updated on 26/Oct/20
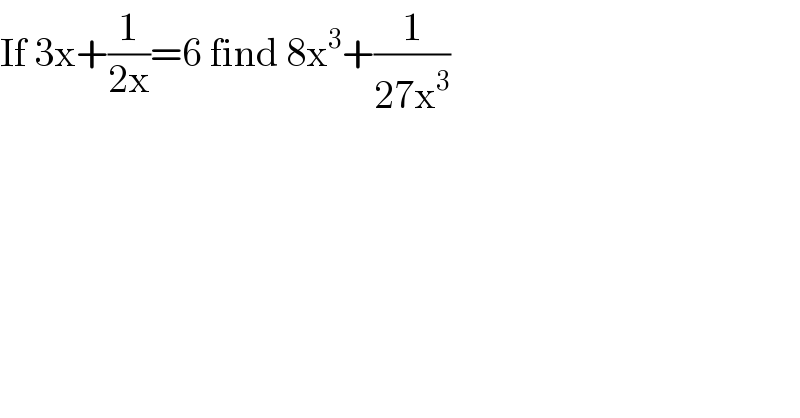
$$\mathrm{If}\:\mathrm{3x}+\frac{\mathrm{1}}{\mathrm{2x}}=\mathrm{6}\:\mathrm{find}\:\mathrm{8x}^{\mathrm{3}} +\frac{\mathrm{1}}{\mathrm{27x}^{\mathrm{3}} } \\ $$
Commented by bemath last updated on 26/Oct/20

$${santuyy} \\ $$
Commented by Jamshidbek2311 last updated on 26/Oct/20
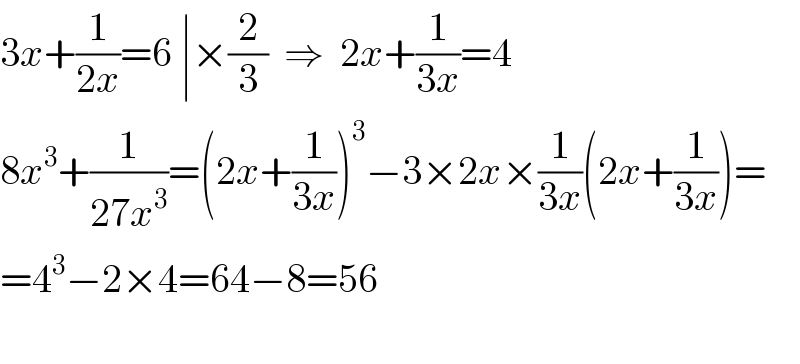
$$\mathrm{3}{x}+\frac{\mathrm{1}}{\mathrm{2}{x}}=\mathrm{6}\:\mid×\frac{\mathrm{2}}{\mathrm{3}}\:\:\Rightarrow\:\:\mathrm{2}{x}+\frac{\mathrm{1}}{\mathrm{3}{x}}=\mathrm{4} \\ $$$$\mathrm{8}{x}^{\mathrm{3}} +\frac{\mathrm{1}}{\mathrm{27}{x}^{\mathrm{3}} }=\left(\mathrm{2}{x}+\frac{\mathrm{1}}{\mathrm{3}{x}}\right)^{\mathrm{3}} −\mathrm{3}×\mathrm{2}{x}×\frac{\mathrm{1}}{\mathrm{3}{x}}\left(\mathrm{2}{x}+\frac{\mathrm{1}}{\mathrm{3}{x}}\right)= \\ $$$$=\mathrm{4}^{\mathrm{3}} −\mathrm{2}×\mathrm{4}=\mathrm{64}−\mathrm{8}=\mathrm{56} \\ $$$$ \\ $$
Commented by som(math1967) last updated on 26/Oct/20

$$\mathrm{Thanks} \\ $$
Answered by Dwaipayan Shikari last updated on 26/Oct/20
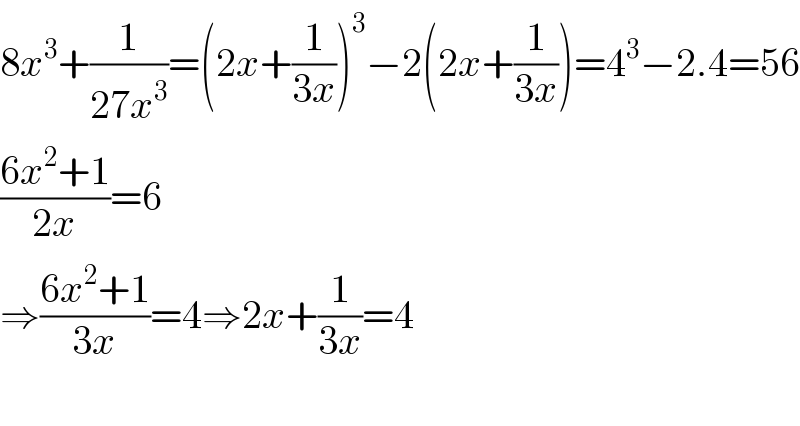
$$\mathrm{8}{x}^{\mathrm{3}} +\frac{\mathrm{1}}{\mathrm{27}{x}^{\mathrm{3}} }=\left(\mathrm{2}{x}+\frac{\mathrm{1}}{\mathrm{3}{x}}\right)^{\mathrm{3}} −\mathrm{2}\left(\mathrm{2}{x}+\frac{\mathrm{1}}{\mathrm{3}{x}}\right)=\mathrm{4}^{\mathrm{3}} −\mathrm{2}.\mathrm{4}=\mathrm{56} \\ $$$$\frac{\mathrm{6}{x}^{\mathrm{2}} +\mathrm{1}}{\mathrm{2}{x}}=\mathrm{6} \\ $$$$\Rightarrow\frac{\mathrm{6}{x}^{\mathrm{2}} +\mathrm{1}}{\mathrm{3}{x}}=\mathrm{4}\Rightarrow\mathrm{2}{x}+\frac{\mathrm{1}}{\mathrm{3}{x}}=\mathrm{4} \\ $$$$ \\ $$
Commented by som(math1967) last updated on 26/Oct/20
$$\mathrm{Very}\:\mathrm{nice}\:\mathrm{thank}\:\mathrm{you} \\ $$
