Question Number 161166 by naka3546 last updated on 13/Dec/21
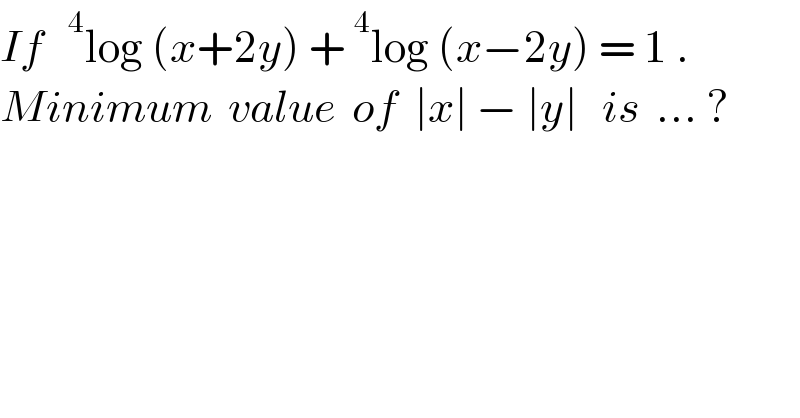
$${If}\:\:\:^{\mathrm{4}} \mathrm{log}\:\left({x}+\mathrm{2}{y}\right)\:+\:^{\mathrm{4}} \mathrm{log}\:\left({x}−\mathrm{2}{y}\right)\:=\:\mathrm{1}\:. \\ $$$${Minimum}\:\:{value}\:\:{of}\:\:\mid{x}\mid\:−\:\mid{y}\mid\:\:\:{is}\:\:…\:? \\ $$
Answered by mr W last updated on 13/Dec/21
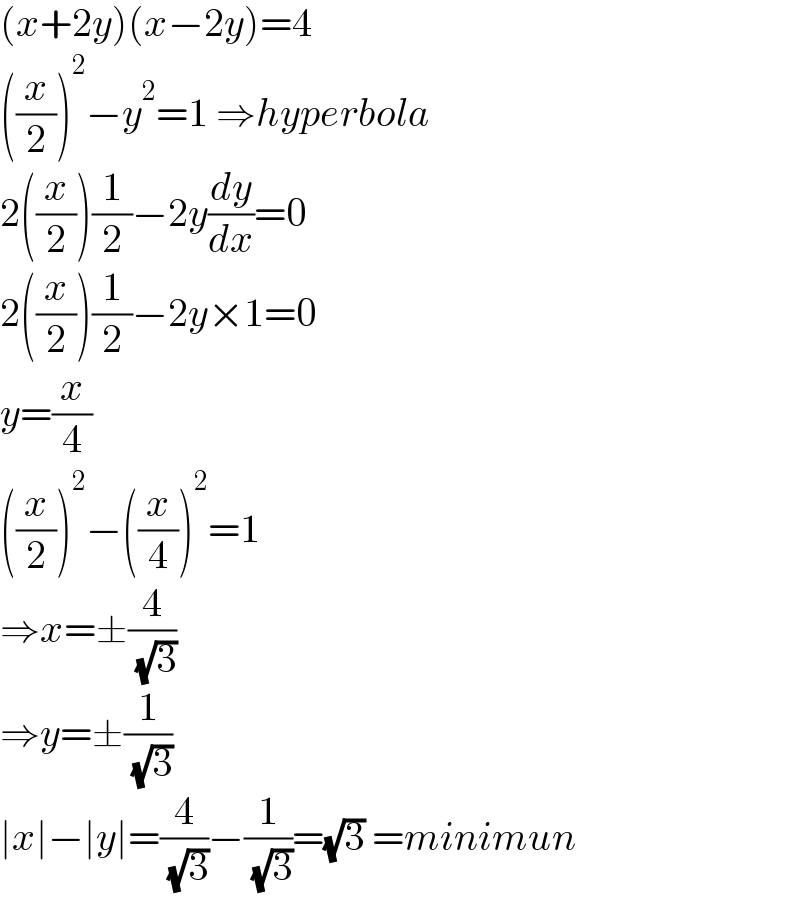
$$\left({x}+\mathrm{2}{y}\right)\left({x}−\mathrm{2}{y}\right)=\mathrm{4} \\ $$$$\left(\frac{{x}}{\mathrm{2}}\right)^{\mathrm{2}} −{y}^{\mathrm{2}} =\mathrm{1}\:\Rightarrow{hyperbola} \\ $$$$\mathrm{2}\left(\frac{{x}}{\mathrm{2}}\right)\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{2}{y}\frac{{dy}}{{dx}}=\mathrm{0} \\ $$$$\mathrm{2}\left(\frac{{x}}{\mathrm{2}}\right)\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{2}{y}×\mathrm{1}=\mathrm{0} \\ $$$${y}=\frac{{x}}{\mathrm{4}} \\ $$$$\left(\frac{{x}}{\mathrm{2}}\right)^{\mathrm{2}} −\left(\frac{{x}}{\mathrm{4}}\right)^{\mathrm{2}} =\mathrm{1} \\ $$$$\Rightarrow{x}=\pm\frac{\mathrm{4}}{\:\sqrt{\mathrm{3}}} \\ $$$$\Rightarrow{y}=\pm\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}} \\ $$$$\mid{x}\mid−\mid{y}\mid=\frac{\mathrm{4}}{\:\sqrt{\mathrm{3}}}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}=\sqrt{\mathrm{3}}\:={minimun} \\ $$
Commented by naka3546 last updated on 13/Dec/21
$${Thank}\:\:{you},\:\:{sir}. \\ $$
