Question Number 174143 by Shrinava last updated on 25/Jul/22
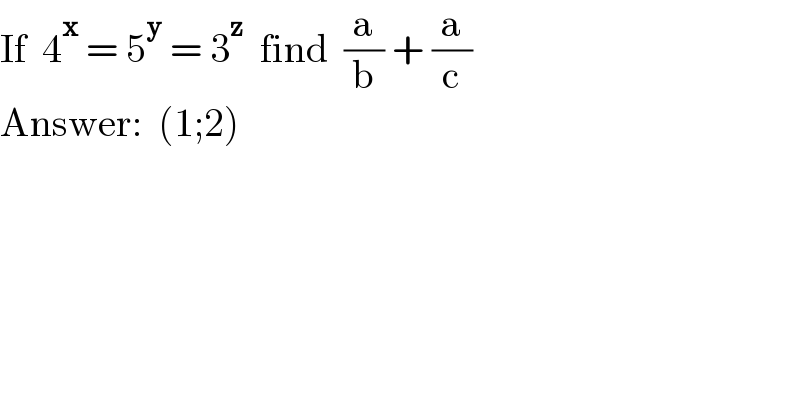
$$\mathrm{If}\:\:\mathrm{4}^{\boldsymbol{\mathrm{x}}} \:=\:\mathrm{5}^{\boldsymbol{\mathrm{y}}} \:=\:\mathrm{3}^{\boldsymbol{\mathrm{z}}} \:\:\mathrm{find}\:\:\frac{\mathrm{a}}{\mathrm{b}}\:+\:\frac{\mathrm{a}}{\mathrm{c}} \\ $$$$\mathrm{Answer}:\:\:\left(\mathrm{1};\mathrm{2}\right) \\ $$
Commented by MJS_new last updated on 26/Jul/22
![does the color of my shirt change the result? only if this apple weighs more than 132.78gr. in this case the answer is [(π,((√2)−(√3)i)),(((v^2 G)/λ_0 ),(lim_(x→∞) (Σ_(n=1) ^x ((1/(n!!)))))) ]](https://www.tinkutara.com/question/Q174151.png)
$$\mathrm{does}\:\mathrm{the}\:\mathrm{color}\:\mathrm{of}\:\mathrm{my}\:\mathrm{shirt}\:\mathrm{change}\:\mathrm{the}\:\mathrm{result}? \\ $$$$\mathrm{only}\:\mathrm{if}\:\mathrm{this}\:\mathrm{apple}\:\mathrm{weighs}\:\mathrm{more}\:\mathrm{than}\:\mathrm{132}.\mathrm{78gr}. \\ $$$$\mathrm{in}\:\mathrm{this}\:\mathrm{case}\:\mathrm{the}\:\mathrm{answer}\:\mathrm{is}\:\begin{bmatrix}{\pi}&{\sqrt{\mathrm{2}}−\sqrt{\mathrm{3}}\mathrm{i}}\\{\frac{{v}^{\mathrm{2}} {G}}{\lambda_{\mathrm{0}} }}&{\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\underset{{n}=\mathrm{1}} {\overset{{x}} {\sum}}\left(\frac{\mathrm{1}}{{n}!!}\right)\right)}\end{bmatrix} \\ $$
Commented by Rasheed.Sindhi last updated on 26/Jul/22
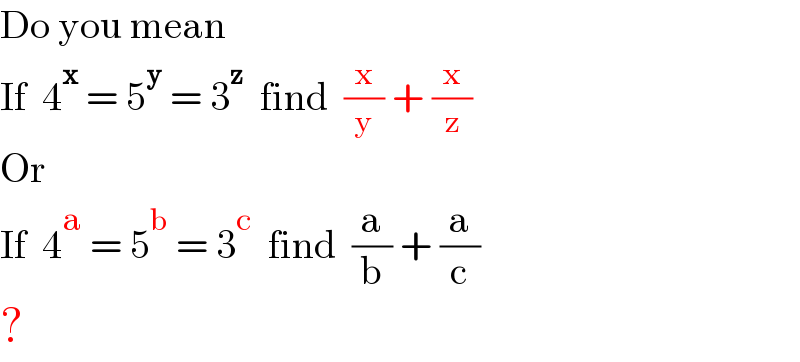
$$\mathrm{Do}\:\mathrm{you}\:\mathrm{mean} \\ $$$$\mathrm{If}\:\:\mathrm{4}^{\boldsymbol{\mathrm{x}}} \:=\:\mathrm{5}^{\boldsymbol{\mathrm{y}}} \:=\:\mathrm{3}^{\boldsymbol{\mathrm{z}}} \:\:\mathrm{find}\:\:\frac{\mathrm{x}}{\mathrm{y}}\:+\:\frac{\mathrm{x}}{\mathrm{z}} \\ $$$$\mathrm{Or} \\ $$$$\mathrm{If}\:\:\mathrm{4}^{\mathrm{a}} \:=\:\mathrm{5}^{\mathrm{b}} \:=\:\mathrm{3}^{\mathrm{c}} \:\:\mathrm{find}\:\:\frac{\mathrm{a}}{\mathrm{b}}\:+\:\frac{\mathrm{a}}{\mathrm{c}} \\ $$$$? \\ $$
Commented by MJS_new last updated on 26/Jul/22
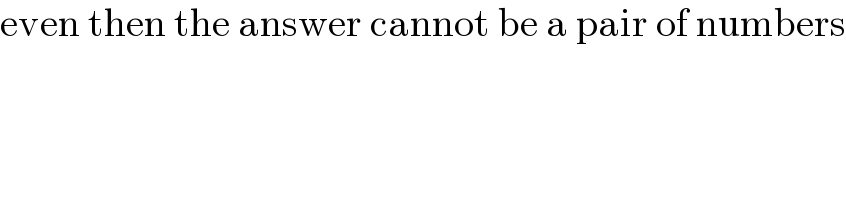
$$\mathrm{even}\:\mathrm{then}\:\mathrm{the}\:\mathrm{answer}\:\mathrm{cannot}\:\mathrm{be}\:\mathrm{a}\:\mathrm{pair}\:\mathrm{of}\:\mathrm{numbers} \\ $$
Commented by Rasheed.Sindhi last updated on 26/Jul/22

$$\mathrm{yes}\:\mathrm{sir} \\ $$
Commented by Shrinava last updated on 26/Jul/22
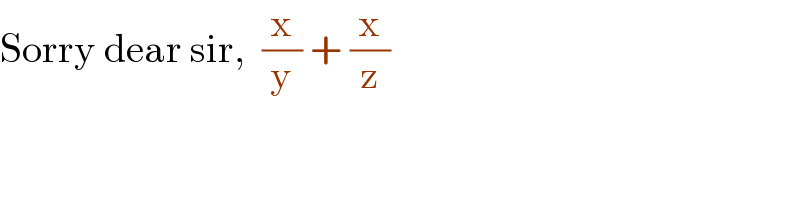
$$\mathrm{Sorry}\:\mathrm{dear}\:\mathrm{sir},\:\:\frac{\mathrm{x}}{\mathrm{y}}\:+\:\frac{\mathrm{x}}{\mathrm{z}} \\ $$
Answered by Rasheed.Sindhi last updated on 26/Jul/22
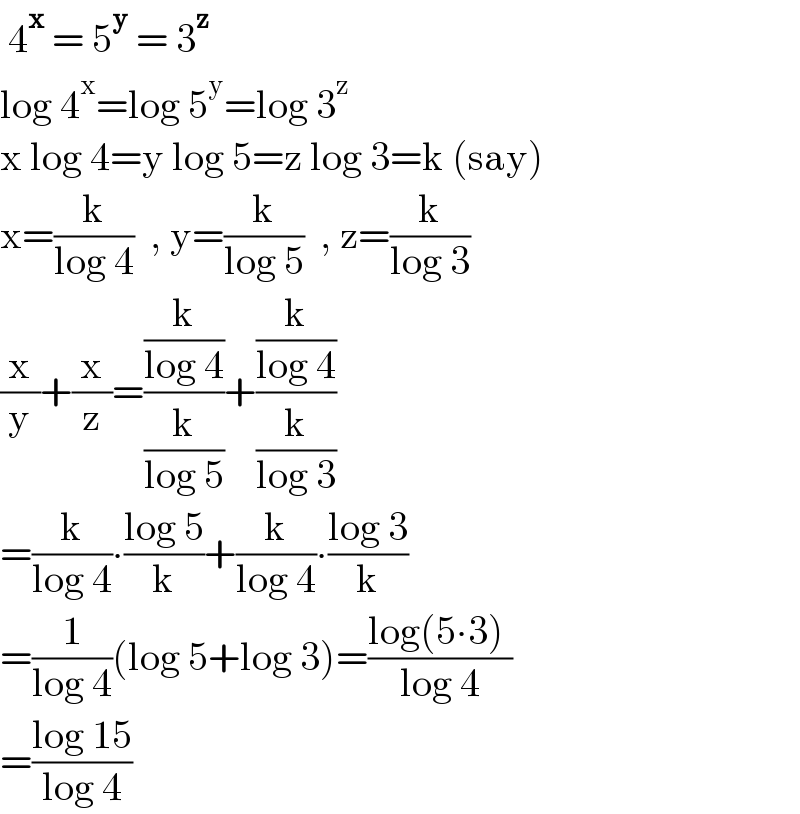
$$\:\mathrm{4}^{\boldsymbol{\mathrm{x}}} \:=\:\mathrm{5}^{\boldsymbol{\mathrm{y}}} \:=\:\mathrm{3}^{\boldsymbol{\mathrm{z}}} \\ $$$$\mathrm{log}\:\mathrm{4}^{\mathrm{x}} =\mathrm{log}\:\mathrm{5}^{\mathrm{y}} =\mathrm{log}\:\mathrm{3}^{\mathrm{z}} \\ $$$$\mathrm{x}\:\mathrm{log}\:\mathrm{4}=\mathrm{y}\:\mathrm{log}\:\mathrm{5}=\mathrm{z}\:\mathrm{log}\:\mathrm{3}=\mathrm{k}\:\left(\mathrm{say}\right) \\ $$$$\mathrm{x}=\frac{\mathrm{k}}{\mathrm{log}\:\mathrm{4}}\:\:,\:\mathrm{y}=\frac{\mathrm{k}}{\mathrm{log}\:\mathrm{5}}\:\:,\:\mathrm{z}=\frac{\mathrm{k}}{\mathrm{log}\:\mathrm{3}} \\ $$$$\frac{\mathrm{x}}{\mathrm{y}}+\frac{\mathrm{x}}{\mathrm{z}}=\frac{\frac{\mathrm{k}}{\mathrm{log}\:\mathrm{4}}}{\frac{\mathrm{k}}{\mathrm{log}\:\mathrm{5}}}+\frac{\frac{\mathrm{k}}{\mathrm{log}\:\mathrm{4}}}{\frac{\mathrm{k}}{\mathrm{log}\:\mathrm{3}}} \\ $$$$=\frac{\mathrm{k}}{\mathrm{log}\:\mathrm{4}}\centerdot\frac{\mathrm{log}\:\mathrm{5}}{\mathrm{k}}+\frac{\mathrm{k}}{\mathrm{log}\:\mathrm{4}}\centerdot\frac{\mathrm{log}\:\mathrm{3}}{\mathrm{k}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{log}\:\mathrm{4}}\left(\mathrm{log}\:\mathrm{5}+\mathrm{log}\:\mathrm{3}\right)=\frac{\mathrm{log}\left(\mathrm{5}\centerdot\mathrm{3}\right)\:}{\mathrm{log}\:\mathrm{4}} \\ $$$$=\frac{\mathrm{log}\:\mathrm{15}}{\mathrm{log}\:\mathrm{4}} \\ $$
Answered by a.lgnaoui last updated on 26/Jul/22
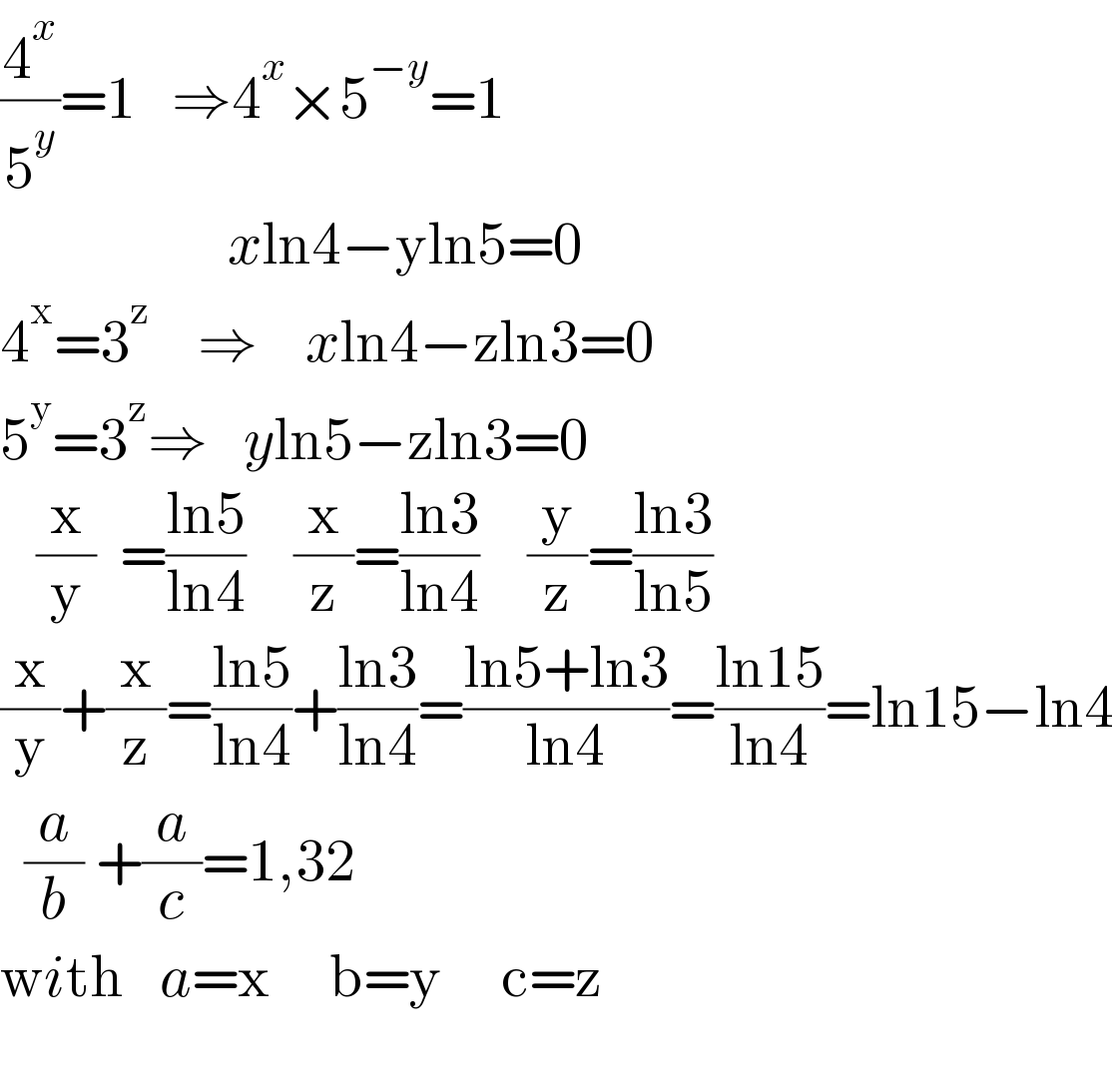
$$\frac{\mathrm{4}^{{x}} }{\mathrm{5}^{{y}} }=\mathrm{1}\:\:\:\Rightarrow\mathrm{4}^{{x}} ×\mathrm{5}^{−{y}} =\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{x}\mathrm{ln4}−\mathrm{yln5}=\mathrm{0}\:\: \\ $$$$\mathrm{4}^{\mathrm{x}} =\mathrm{3}^{\mathrm{z}} \:\:\:\:\Rightarrow\:\:\:\:{x}\mathrm{ln4}−\mathrm{zln3}=\mathrm{0} \\ $$$$\mathrm{5}^{\mathrm{y}} =\mathrm{3}^{\mathrm{z}} \Rightarrow\:\:\:{y}\mathrm{ln5}−\mathrm{zln3}=\mathrm{0} \\ $$$$\:\:\:\frac{\mathrm{x}}{\mathrm{y}}\:\:=\frac{\mathrm{ln5}}{\mathrm{ln4}}\:\:\:\:\frac{\mathrm{x}}{\mathrm{z}}=\frac{\mathrm{ln3}}{\mathrm{ln4}}\:\:\:\:\frac{\mathrm{y}}{\mathrm{z}}=\frac{\mathrm{ln3}}{\mathrm{ln5}} \\ $$$$\frac{\mathrm{x}}{\mathrm{y}}+\frac{\mathrm{x}}{\mathrm{z}}=\frac{\mathrm{ln5}}{\mathrm{ln4}}+\frac{\mathrm{ln3}}{\mathrm{ln4}}=\frac{\mathrm{ln5}+\mathrm{ln3}}{\mathrm{ln4}}=\frac{\mathrm{ln15}}{\mathrm{ln4}}=\mathrm{ln15}−\mathrm{ln4} \\ $$$$\:\:\frac{{a}}{{b}}\:+\frac{{a}}{{c}}=\mathrm{1},\mathrm{32} \\ $$$$\mathrm{w}{i}\mathrm{th}\:\:\:{a}=\mathrm{x}\:\:\:\:\:\mathrm{b}=\mathrm{y}\:\:\:\:\:\mathrm{c}=\mathrm{z} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$
