Question Number 24933 by adityapratap2585@gmail.com last updated on 29/Nov/17
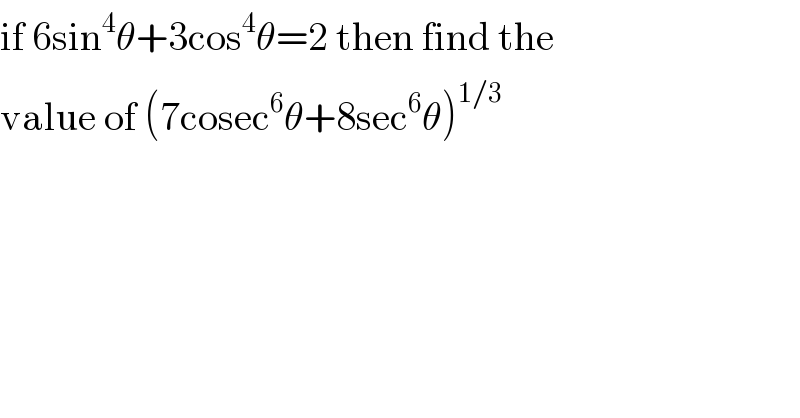
$$\mathrm{if}\:\mathrm{6sin}^{\mathrm{4}} \theta+\mathrm{3cos}^{\mathrm{4}} \theta=\mathrm{2}\:\mathrm{then}\:\mathrm{find}\:\mathrm{the} \\ $$$$\mathrm{value}\:\mathrm{of}\:\left(\mathrm{7cosec}^{\mathrm{6}} \theta+\mathrm{8sec}^{\mathrm{6}} \theta\right)^{\mathrm{1}/\mathrm{3}} \\ $$
Commented by prakash jain last updated on 29/Nov/17
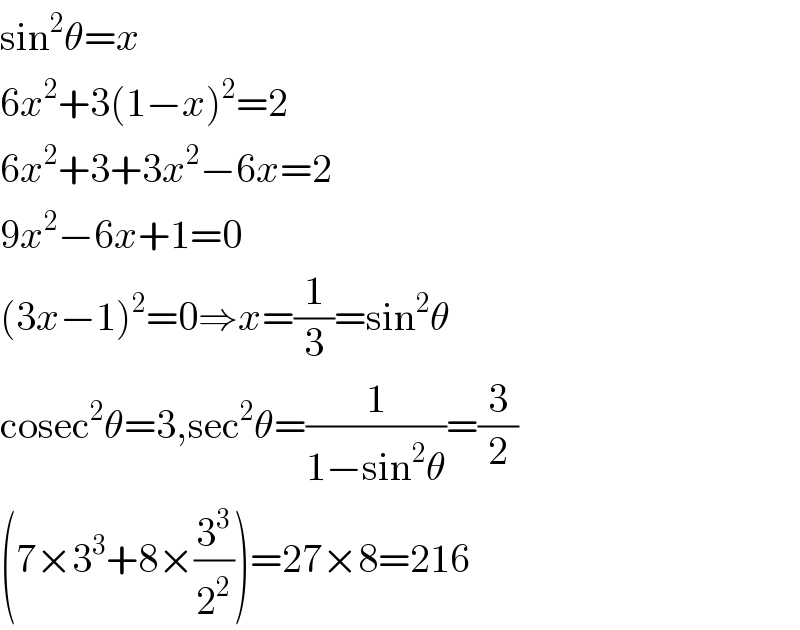
$$\mathrm{sin}^{\mathrm{2}} \theta={x} \\ $$$$\mathrm{6}{x}^{\mathrm{2}} +\mathrm{3}\left(\mathrm{1}−{x}\right)^{\mathrm{2}} =\mathrm{2} \\ $$$$\mathrm{6}{x}^{\mathrm{2}} +\mathrm{3}+\mathrm{3}{x}^{\mathrm{2}} −\mathrm{6}{x}=\mathrm{2} \\ $$$$\mathrm{9}{x}^{\mathrm{2}} −\mathrm{6}{x}+\mathrm{1}=\mathrm{0} \\ $$$$\left(\mathrm{3}{x}−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{0}\Rightarrow{x}=\frac{\mathrm{1}}{\mathrm{3}}=\mathrm{sin}^{\mathrm{2}} \theta \\ $$$$\mathrm{cosec}^{\mathrm{2}} \theta=\mathrm{3},\mathrm{sec}^{\mathrm{2}} \theta=\frac{\mathrm{1}}{\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \theta}=\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\left(\mathrm{7}×\mathrm{3}^{\mathrm{3}} +\mathrm{8}×\frac{\mathrm{3}^{\mathrm{3}} }{\mathrm{2}^{\mathrm{2}} }\right)=\mathrm{27}×\mathrm{8}=\mathrm{216} \\ $$
Commented by adityapratap2585@gmail.com last updated on 29/Nov/17

$$\mathrm{thanks}\:\mathrm{sir} \\ $$
