Question Number 112542 by bobhans last updated on 08/Sep/20
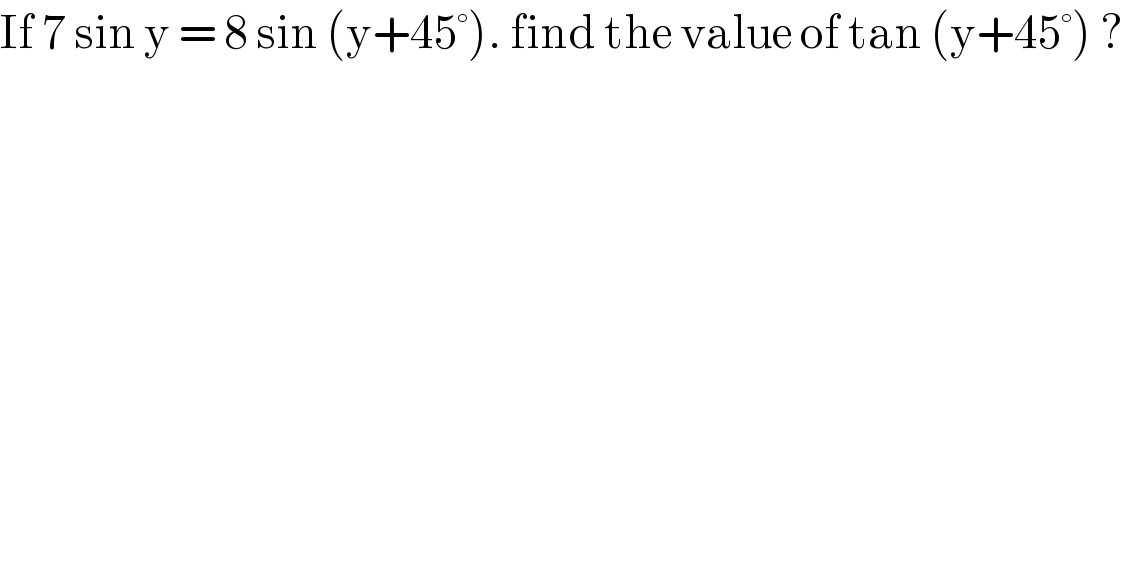
$$\mathrm{If}\:\mathrm{7}\:\mathrm{sin}\:\mathrm{y}\:=\:\mathrm{8}\:\mathrm{sin}\:\left(\mathrm{y}+\mathrm{45}°\right).\:\mathrm{find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{tan}\:\left(\mathrm{y}+\mathrm{45}°\right)\:? \\ $$
Answered by bemath last updated on 08/Sep/20
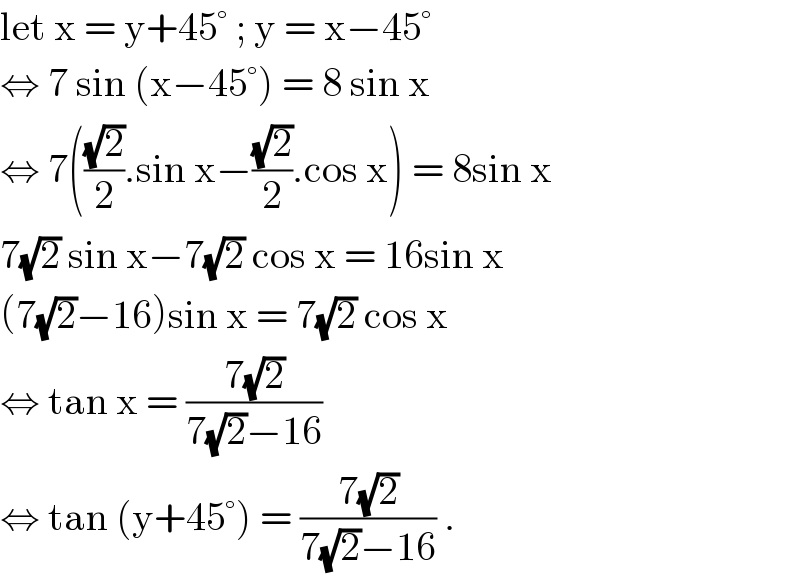
$$\mathrm{let}\:\mathrm{x}\:=\:\mathrm{y}+\mathrm{45}°\:;\:\mathrm{y}\:=\:\mathrm{x}−\mathrm{45}° \\ $$$$\Leftrightarrow\:\mathrm{7}\:\mathrm{sin}\:\left(\mathrm{x}−\mathrm{45}°\right)\:=\:\mathrm{8}\:\mathrm{sin}\:\mathrm{x} \\ $$$$\Leftrightarrow\:\mathrm{7}\left(\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}.\mathrm{sin}\:\mathrm{x}−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}.\mathrm{cos}\:\mathrm{x}\right)\:=\:\mathrm{8sin}\:\mathrm{x} \\ $$$$\mathrm{7}\sqrt{\mathrm{2}}\:\mathrm{sin}\:\mathrm{x}−\mathrm{7}\sqrt{\mathrm{2}}\:\mathrm{cos}\:\mathrm{x}\:=\:\mathrm{16sin}\:\mathrm{x} \\ $$$$\left(\mathrm{7}\sqrt{\mathrm{2}}−\mathrm{16}\right)\mathrm{sin}\:\mathrm{x}\:=\:\mathrm{7}\sqrt{\mathrm{2}}\:\mathrm{cos}\:\mathrm{x} \\ $$$$\Leftrightarrow\:\mathrm{tan}\:\mathrm{x}\:=\:\frac{\mathrm{7}\sqrt{\mathrm{2}}}{\mathrm{7}\sqrt{\mathrm{2}}−\mathrm{16}} \\ $$$$\Leftrightarrow\:\mathrm{tan}\:\left(\mathrm{y}+\mathrm{45}°\right)\:=\:\frac{\mathrm{7}\sqrt{\mathrm{2}}}{\mathrm{7}\sqrt{\mathrm{2}}−\mathrm{16}}\:. \\ $$
