Question Number 116483 by bemath last updated on 04/Oct/20
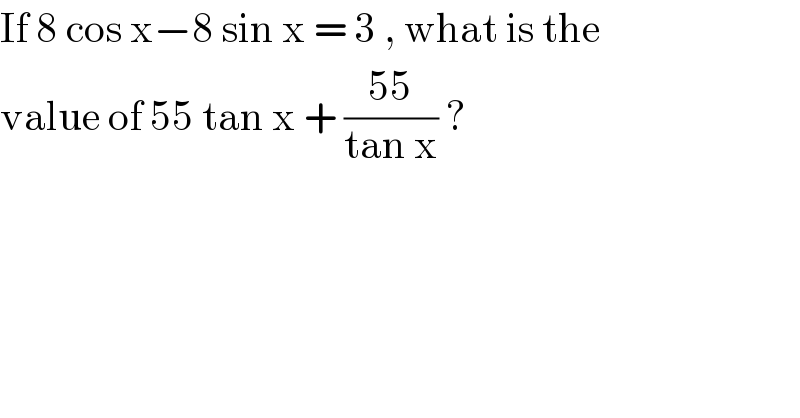
$$\mathrm{If}\:\mathrm{8}\:\mathrm{cos}\:\mathrm{x}−\mathrm{8}\:\mathrm{sin}\:\mathrm{x}\:=\:\mathrm{3}\:,\:\mathrm{what}\:\mathrm{is}\:\mathrm{the}\: \\ $$$$\mathrm{value}\:\mathrm{of}\:\mathrm{55}\:\mathrm{tan}\:\mathrm{x}\:+\:\frac{\mathrm{55}}{\mathrm{tan}\:\mathrm{x}}\:? \\ $$
Answered by mr W last updated on 04/Oct/20
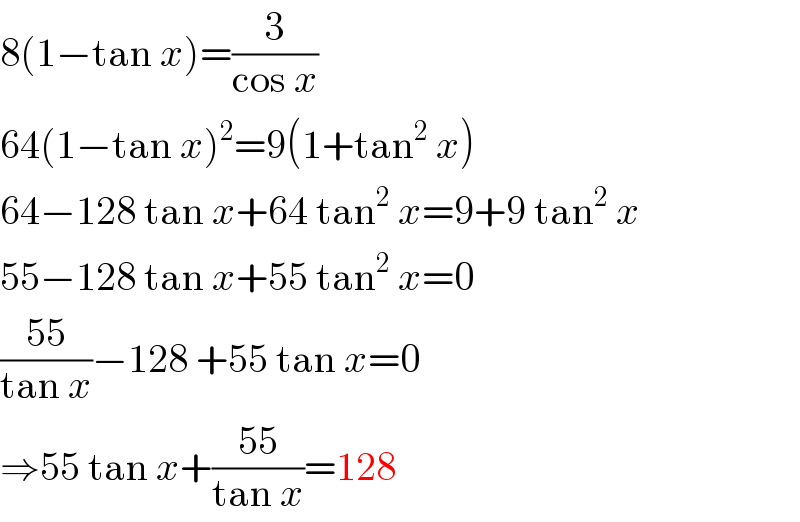
$$\mathrm{8}\left(\mathrm{1}−\mathrm{tan}\:{x}\right)=\frac{\mathrm{3}}{\mathrm{cos}\:{x}} \\ $$$$\mathrm{64}\left(\mathrm{1}−\mathrm{tan}\:{x}\right)^{\mathrm{2}} =\mathrm{9}\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:{x}\right) \\ $$$$\mathrm{64}−\mathrm{128}\:\mathrm{tan}\:{x}+\mathrm{64}\:\mathrm{tan}^{\mathrm{2}} \:{x}=\mathrm{9}+\mathrm{9}\:\mathrm{tan}^{\mathrm{2}} \:{x} \\ $$$$\mathrm{55}−\mathrm{128}\:\mathrm{tan}\:{x}+\mathrm{55}\:\mathrm{tan}^{\mathrm{2}} \:{x}=\mathrm{0} \\ $$$$\frac{\mathrm{55}}{\mathrm{tan}\:{x}}−\mathrm{128}\:+\mathrm{55}\:\mathrm{tan}\:{x}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{55}\:\mathrm{tan}\:{x}+\frac{\mathrm{55}}{\mathrm{tan}\:{x}}=\mathrm{128} \\ $$
Answered by bobhans last updated on 04/Oct/20
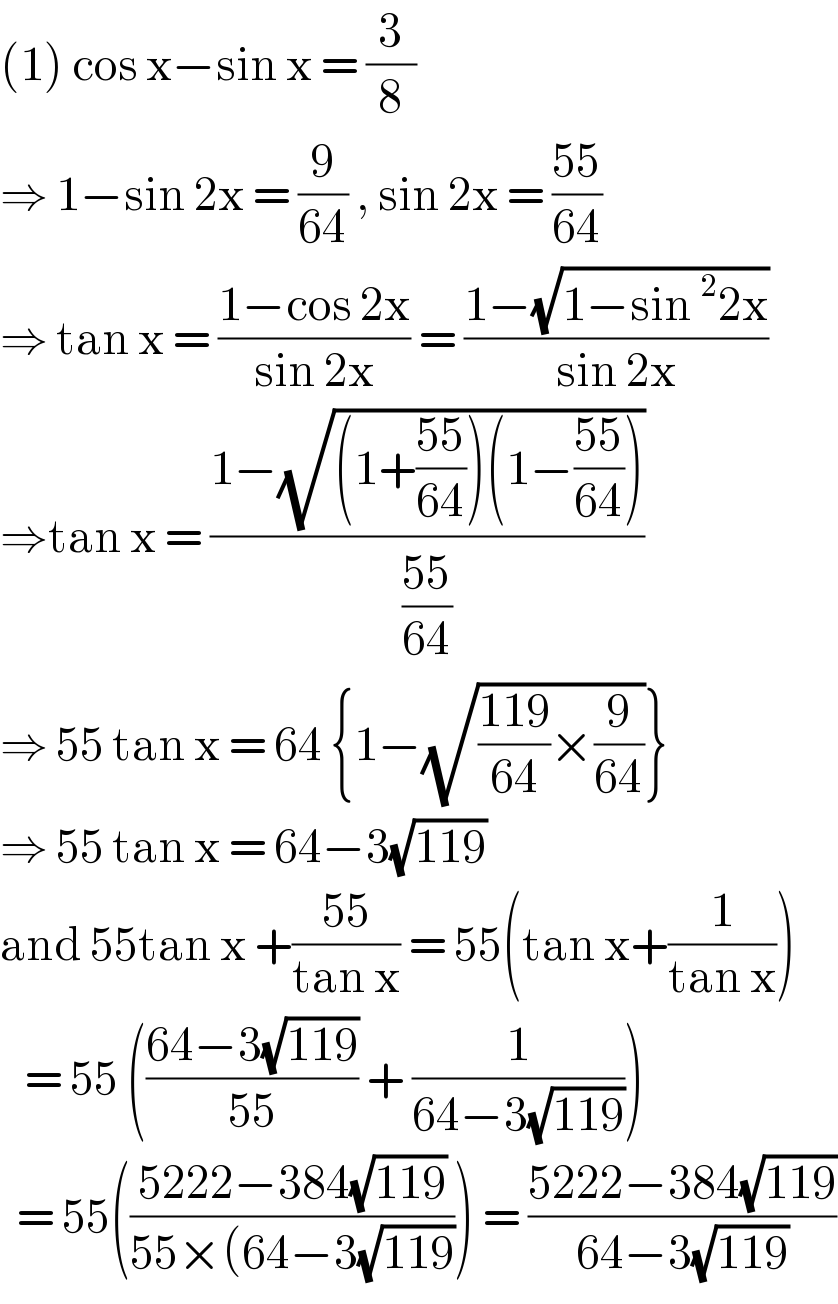
$$\left(\mathrm{1}\right)\:\mathrm{cos}\:\mathrm{x}−\mathrm{sin}\:\mathrm{x}\:=\:\frac{\mathrm{3}}{\mathrm{8}} \\ $$$$\Rightarrow\:\mathrm{1}−\mathrm{sin}\:\mathrm{2x}\:=\:\frac{\mathrm{9}}{\mathrm{64}}\:,\:\mathrm{sin}\:\mathrm{2x}\:=\:\frac{\mathrm{55}}{\mathrm{64}} \\ $$$$\Rightarrow\:\mathrm{tan}\:\mathrm{x}\:=\:\frac{\mathrm{1}−\mathrm{cos}\:\mathrm{2x}}{\mathrm{sin}\:\mathrm{2x}}\:=\:\frac{\mathrm{1}−\sqrt{\mathrm{1}−\mathrm{sin}\:^{\mathrm{2}} \mathrm{2x}}}{\mathrm{sin}\:\mathrm{2x}} \\ $$$$\Rightarrow\mathrm{tan}\:\mathrm{x}\:=\:\frac{\mathrm{1}−\sqrt{\left(\mathrm{1}+\frac{\mathrm{55}}{\mathrm{64}}\right)\left(\mathrm{1}−\frac{\mathrm{55}}{\mathrm{64}}\right)}}{\frac{\mathrm{55}}{\mathrm{64}}} \\ $$$$\Rightarrow\:\mathrm{55}\:\mathrm{tan}\:\mathrm{x}\:=\:\mathrm{64}\:\left\{\mathrm{1}−\sqrt{\frac{\mathrm{119}}{\mathrm{64}}×\frac{\mathrm{9}}{\mathrm{64}}}\right\} \\ $$$$\Rightarrow\:\mathrm{55}\:\mathrm{tan}\:\mathrm{x}\:=\:\mathrm{64}−\mathrm{3}\sqrt{\mathrm{119}}\: \\ $$$$\mathrm{and}\:\mathrm{55tan}\:\mathrm{x}\:+\frac{\mathrm{55}}{\mathrm{tan}\:\mathrm{x}}\:=\:\mathrm{55}\left(\mathrm{tan}\:\mathrm{x}+\frac{\mathrm{1}}{\mathrm{tan}\:\mathrm{x}}\right) \\ $$$$\:\:\:=\:\mathrm{55}\:\left(\frac{\mathrm{64}−\mathrm{3}\sqrt{\mathrm{119}}}{\mathrm{55}}\:+\:\frac{\mathrm{1}}{\mathrm{64}−\mathrm{3}\sqrt{\mathrm{119}}}\right) \\ $$$$\:\:=\:\mathrm{55}\left(\frac{\mathrm{5222}−\mathrm{384}\sqrt{\mathrm{119}}}{\mathrm{55}×\left(\mathrm{64}−\mathrm{3}\sqrt{\mathrm{119}}\right.}\right)\:=\:\frac{\mathrm{5222}−\mathrm{384}\sqrt{\mathrm{119}}}{\mathrm{64}−\mathrm{3}\sqrt{\mathrm{119}}} \\ $$
