Question Number 115018 by bemath last updated on 23/Sep/20
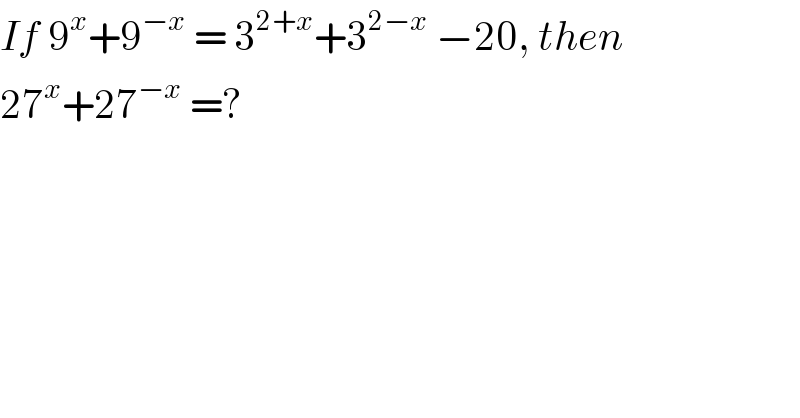
$${If}\:\mathrm{9}^{{x}} +\mathrm{9}^{−{x}} \:=\:\mathrm{3}^{\mathrm{2}+{x}} +\mathrm{3}^{\mathrm{2}−{x}} \:−\mathrm{20},\:{then}\: \\ $$$$\mathrm{27}^{{x}} +\mathrm{27}^{−{x}} \:=? \\ $$
Answered by bobhans last updated on 23/Sep/20
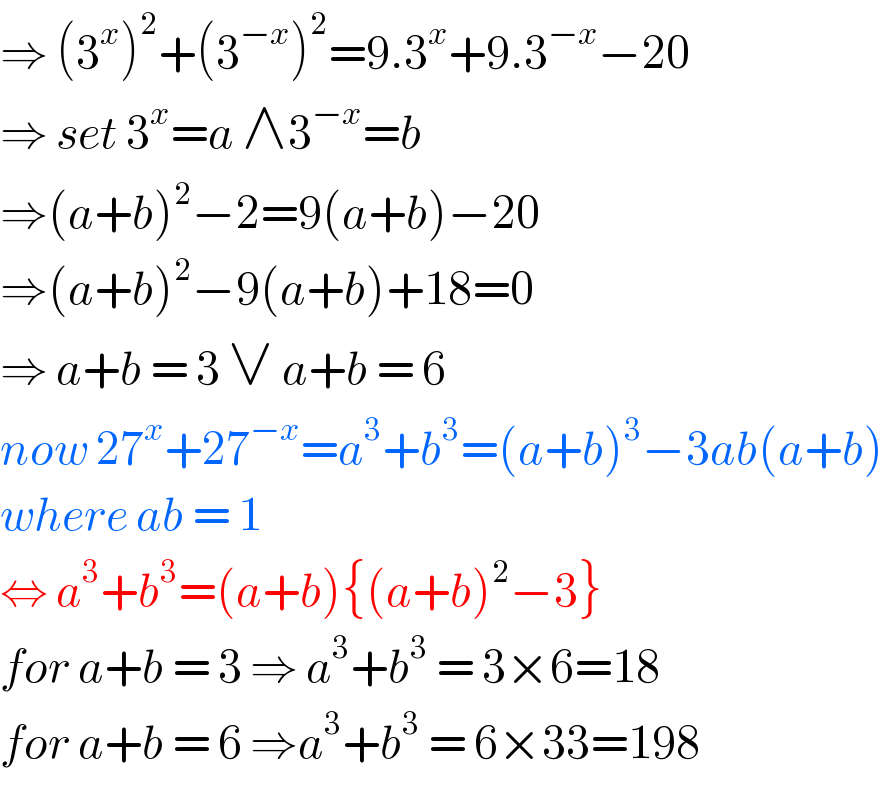
$$\Rightarrow\:\left(\mathrm{3}^{{x}} \right)^{\mathrm{2}} +\left(\mathrm{3}^{−{x}} \right)^{\mathrm{2}} =\mathrm{9}.\mathrm{3}^{{x}} +\mathrm{9}.\mathrm{3}^{−{x}} −\mathrm{20} \\ $$$$\Rightarrow\:{set}\:\mathrm{3}^{{x}} ={a}\:\wedge\mathrm{3}^{−{x}} ={b} \\ $$$$\Rightarrow\left({a}+{b}\right)^{\mathrm{2}} −\mathrm{2}=\mathrm{9}\left({a}+{b}\right)−\mathrm{20} \\ $$$$\Rightarrow\left({a}+{b}\right)^{\mathrm{2}} −\mathrm{9}\left({a}+{b}\right)+\mathrm{18}=\mathrm{0} \\ $$$$\Rightarrow\:{a}+{b}\:=\:\mathrm{3}\:\vee\:{a}+{b}\:=\:\mathrm{6} \\ $$$${now}\:\mathrm{27}^{{x}} +\mathrm{27}^{−{x}} ={a}^{\mathrm{3}} +{b}^{\mathrm{3}} =\left({a}+{b}\right)^{\mathrm{3}} −\mathrm{3}{ab}\left({a}+{b}\right) \\ $$$${where}\:{ab}\:=\:\mathrm{1} \\ $$$$\Leftrightarrow\:{a}^{\mathrm{3}} +{b}^{\mathrm{3}} =\left({a}+{b}\right)\left\{\left({a}+{b}\right)^{\mathrm{2}} −\mathrm{3}\right\} \\ $$$${for}\:{a}+{b}\:=\:\mathrm{3}\:\Rightarrow\:{a}^{\mathrm{3}} +{b}^{\mathrm{3}} \:=\:\mathrm{3}×\mathrm{6}=\mathrm{18}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$${for}\:{a}+{b}\:=\:\mathrm{6}\:\Rightarrow{a}^{\mathrm{3}} +{b}^{\mathrm{3}} \:=\:\mathrm{6}×\mathrm{33}=\mathrm{198} \\ $$
Answered by PRITHWISH SEN 2 last updated on 23/Sep/20
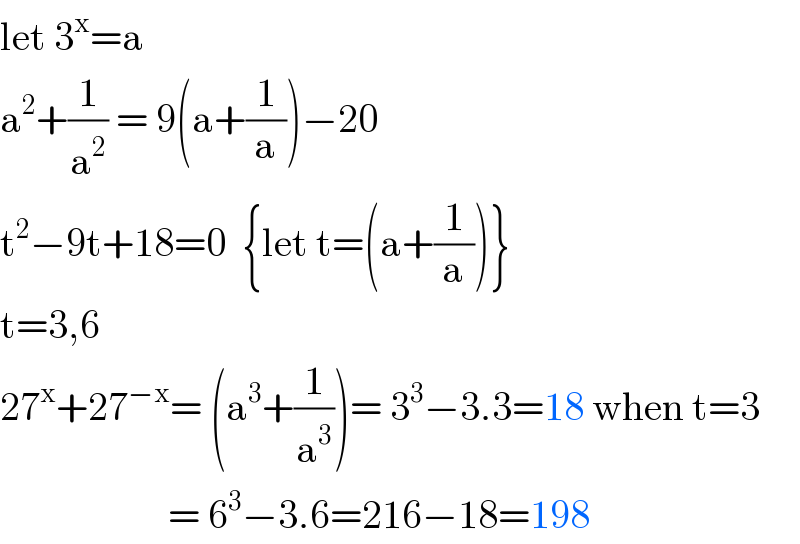
$$\mathrm{let}\:\mathrm{3}^{\mathrm{x}} =\mathrm{a} \\ $$$$\mathrm{a}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{2}} }\:=\:\mathrm{9}\left(\mathrm{a}+\frac{\mathrm{1}}{\mathrm{a}}\right)−\mathrm{20} \\ $$$$\mathrm{t}^{\mathrm{2}} −\mathrm{9t}+\mathrm{18}=\mathrm{0}\:\:\left\{\mathrm{let}\:\mathrm{t}=\left(\mathrm{a}+\frac{\mathrm{1}}{\mathrm{a}}\right)\right\} \\ $$$$\mathrm{t}=\mathrm{3},\mathrm{6} \\ $$$$\mathrm{27}^{\mathrm{x}} +\mathrm{27}^{−\mathrm{x}} =\:\left(\mathrm{a}^{\mathrm{3}} +\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{3}} }\right)=\:\mathrm{3}^{\mathrm{3}} −\mathrm{3}.\mathrm{3}=\mathrm{18}\:\mathrm{when}\:\mathrm{t}=\mathrm{3} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{6}^{\mathrm{3}} −\mathrm{3}.\mathrm{6}=\mathrm{216}−\mathrm{18}=\mathrm{198} \\ $$
