Menu Close

if-9x-2-1-x-2-3-then-27x-3-1-x-3-

Tinku Tara 0 Comments
Pin




Question Number 161169 by MathsFan last updated on 13/Dec/21
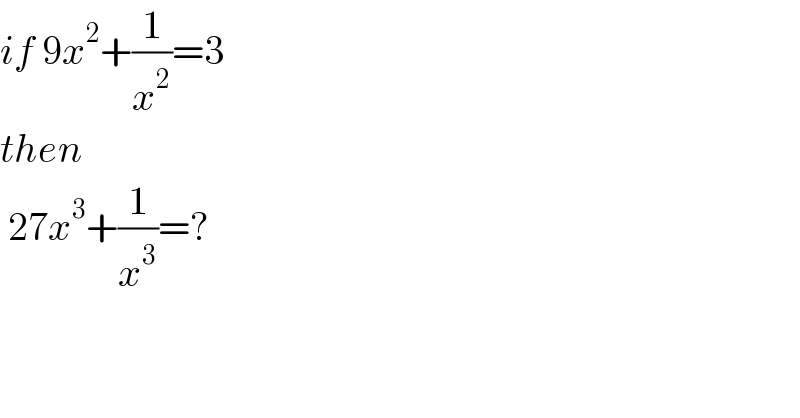
if 9x^2 +(1/x^2 )=3 then 27x^3 +(1/x^3 )=?
$${if}\:\mathrm{9}{x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }=\mathrm{3} \\ $$$${then} \\ $$$$\:\mathrm{27}{x}^{\mathrm{3}} +\frac{\mathrm{1}}{{x}^{\mathrm{3}} }=? \\ $$
Answered by Rasheed.Sindhi last updated on 13/Dec/21
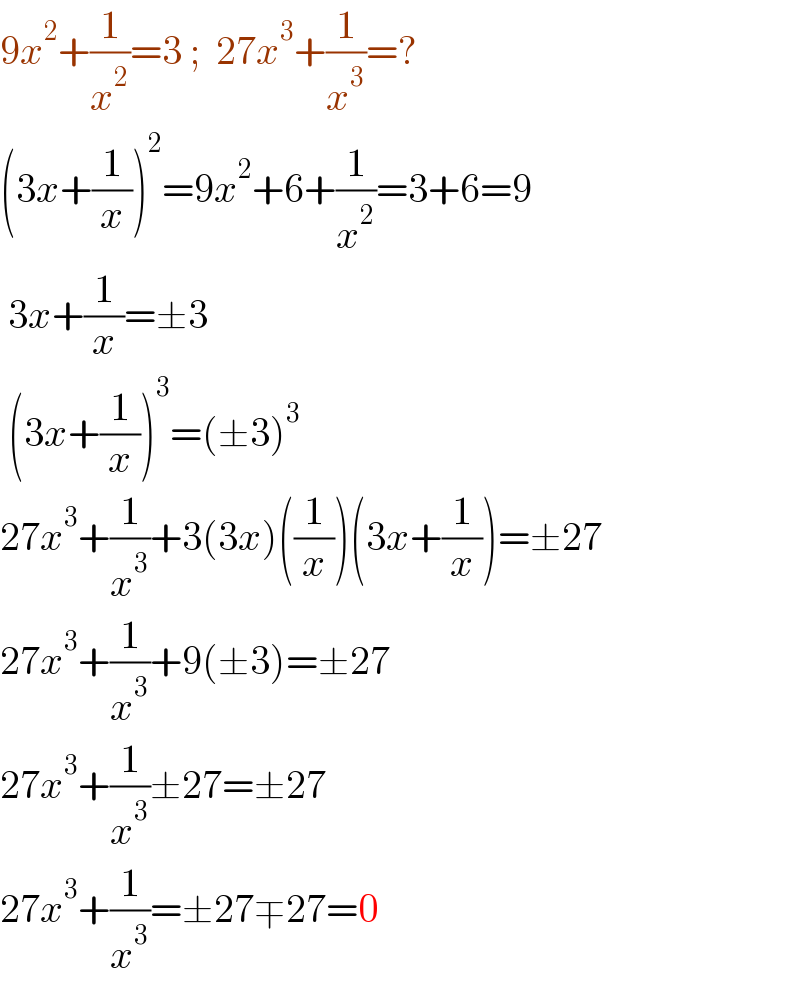
9x^2 +(1/x^2 )=3 ; 27x^3 +(1/x^3 )=? (3x+(1/x))^2 =9x^2 +6+(1/x^2 )=3+6=9 3x+(1/x)=±3 (3x+(1/x))^3 =(±3)^3 27x^3 +(1/x^3 )+3(3x)((1/x))(3x+(1/x))=±27 27x^3 +(1/x^3 )+9(±3)=±27 27x^3 +(1/x^3 )±27=±27 27x^3 +(1/x^3 )=±27∓27=0
$$\mathrm{9}{x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }=\mathrm{3}\:;\:\:\mathrm{27}{x}^{\mathrm{3}} +\frac{\mathrm{1}}{{x}^{\mathrm{3}} }=? \\ $$$$\left(\mathrm{3}{x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} =\mathrm{9}{x}^{\mathrm{2}} +\mathrm{6}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }=\mathrm{3}+\mathrm{6}=\mathrm{9} \\ $$$$\:\mathrm{3}{x}+\frac{\mathrm{1}}{{x}}=\pm\mathrm{3} \\ $$$$\:\left(\mathrm{3}{x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{3}} =\left(\pm\mathrm{3}\right)^{\mathrm{3}} \\ $$$$\mathrm{27}{x}^{\mathrm{3}} +\frac{\mathrm{1}}{{x}^{\mathrm{3}} }+\mathrm{3}\left(\mathrm{3}{x}\right)\left(\frac{\mathrm{1}}{{x}}\right)\left(\mathrm{3}{x}+\frac{\mathrm{1}}{{x}}\right)=\pm\mathrm{27} \\ $$$$\mathrm{27}{x}^{\mathrm{3}} +\frac{\mathrm{1}}{{x}^{\mathrm{3}} }+\mathrm{9}\left(\pm\mathrm{3}\right)=\pm\mathrm{27} \\ $$$$\mathrm{27}{x}^{\mathrm{3}} +\frac{\mathrm{1}}{{x}^{\mathrm{3}} }\pm\mathrm{27}=\pm\mathrm{27} \\ $$$$\mathrm{27}{x}^{\mathrm{3}} +\frac{\mathrm{1}}{{x}^{\mathrm{3}} }=\pm\mathrm{27}\mp\mathrm{27}=\mathrm{0} \\ $$
Answered by Rasheed.Sindhi last updated on 15/Dec/21
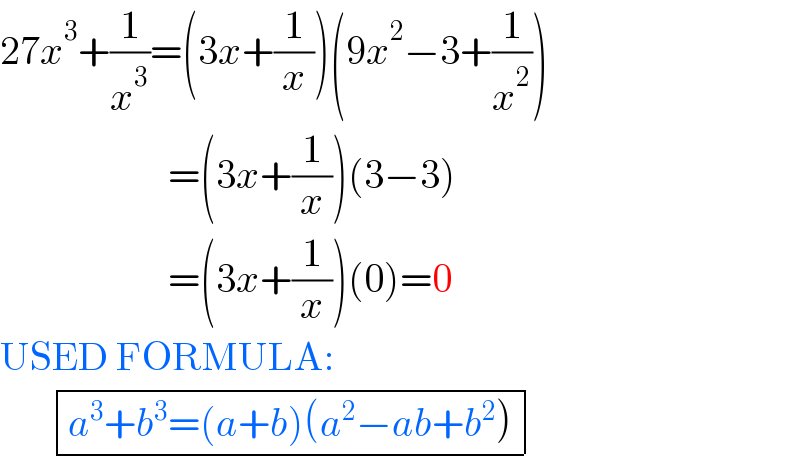
27x^3 +(1/x^3 )=(3x+(1/x))(9x^2 −3+(1/x^2 )) =(3x+(1/x))(3−3) =(3x+(1/x))(0)=0 USED FORMULA: determinant (((a^3 +b^3 =(a+b)(a^2 −ab+b^2 ))))
$$\mathrm{27}{x}^{\mathrm{3}} +\frac{\mathrm{1}}{{x}^{\mathrm{3}} }=\left(\mathrm{3}{x}+\frac{\mathrm{1}}{{x}}\right)\left(\mathrm{9}{x}^{\mathrm{2}} −\mathrm{3}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\left(\mathrm{3}{x}+\frac{\mathrm{1}}{{x}}\right)\left(\mathrm{3}−\mathrm{3}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\left(\mathrm{3}{x}+\frac{\mathrm{1}}{{x}}\right)\left(\mathrm{0}\right)=\mathrm{0} \\ $$$$\mathrm{USED}\:\mathrm{FORMULA}: \\ $$$$\:\:\:\:\:\:\:\:\begin{array}{|c|}{{a}^{\mathrm{3}} +{b}^{\mathrm{3}} =\left({a}+{b}\right)\left({a}^{\mathrm{2}} −{ab}+{b}^{\mathrm{2}} \right)}\\\hline\end{array}\: \\ $$
Commented by MathsFan last updated on 13/Dec/21
thank you sir.
$${thank}\:{you}\:{sir}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *