Question Number 22061 by NECx last updated on 10/Oct/17
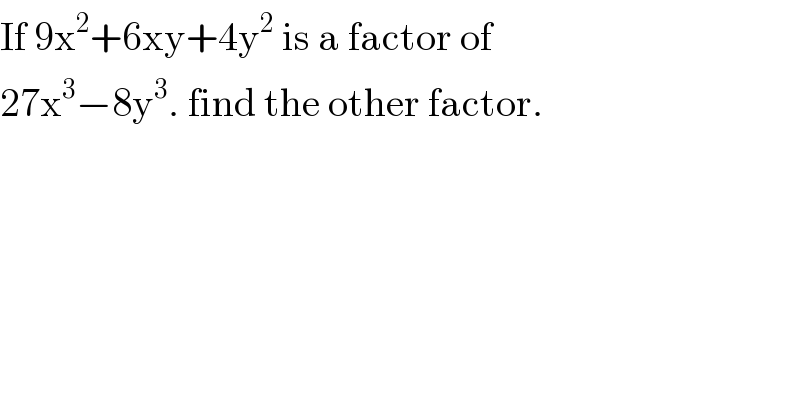
$$\mathrm{If}\:\mathrm{9x}^{\mathrm{2}} +\mathrm{6xy}+\mathrm{4y}^{\mathrm{2}} \:\mathrm{is}\:\mathrm{a}\:\mathrm{factor}\:\mathrm{of} \\ $$$$\mathrm{27x}^{\mathrm{3}} −\mathrm{8y}^{\mathrm{3}} .\:\mathrm{find}\:\mathrm{the}\:\mathrm{other}\:\mathrm{factor}. \\ $$
Answered by sma3l2996 last updated on 10/Oct/17
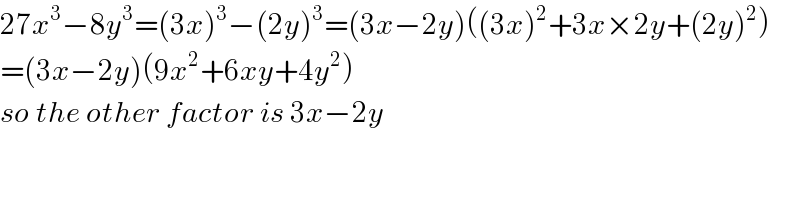
$$\mathrm{27}{x}^{\mathrm{3}} −\mathrm{8}{y}^{\mathrm{3}} =\left(\mathrm{3}{x}\right)^{\mathrm{3}} −\left(\mathrm{2}{y}\right)^{\mathrm{3}} =\left(\mathrm{3}{x}−\mathrm{2}{y}\right)\left(\left(\mathrm{3}{x}\right)^{\mathrm{2}} +\mathrm{3}{x}×\mathrm{2}{y}+\left(\mathrm{2}{y}\right)^{\mathrm{2}} \right) \\ $$$$=\left(\mathrm{3}{x}−\mathrm{2}{y}\right)\left(\mathrm{9}{x}^{\mathrm{2}} +\mathrm{6}{xy}+\mathrm{4}{y}^{\mathrm{2}} \right) \\ $$$${so}\:{the}\:{other}\:{factor}\:{is}\:\mathrm{3}{x}−\mathrm{2}{y} \\ $$
