Question Number 92557 by I want to learn more last updated on 07/May/20
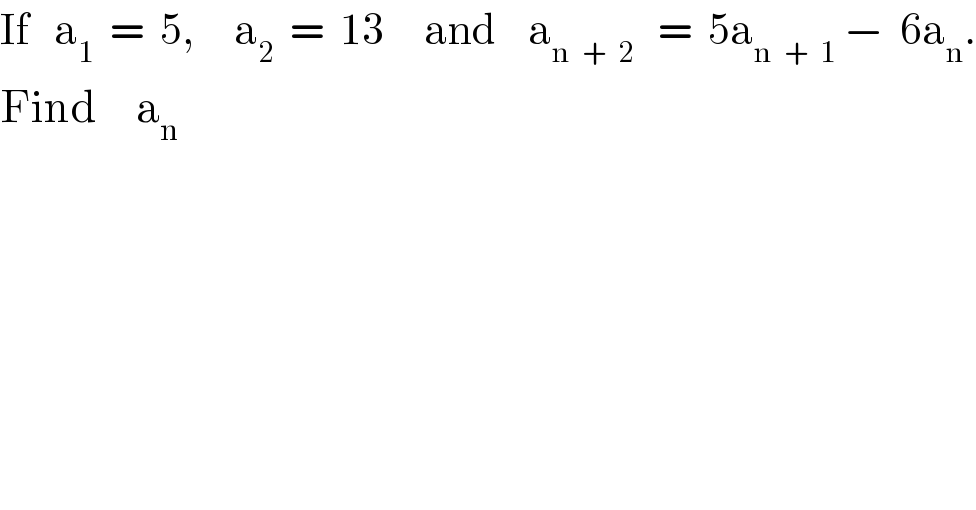
$$\mathrm{If}\:\:\:\mathrm{a}_{\mathrm{1}} \:\:=\:\:\mathrm{5},\:\:\:\:\:\mathrm{a}_{\mathrm{2}} \:\:=\:\:\mathrm{13}\:\:\:\:\:\mathrm{and}\:\:\:\:\mathrm{a}_{\mathrm{n}\:\:+\:\:\mathrm{2}} \:\:\:=\:\:\mathrm{5a}_{\mathrm{n}\:\:+\:\:\mathrm{1}} \:−\:\:\mathrm{6a}_{\mathrm{n}} . \\ $$$$\mathrm{Find}\:\:\:\:\:\mathrm{a}_{\mathrm{n}} \\ $$
Commented by prakash jain last updated on 07/May/20
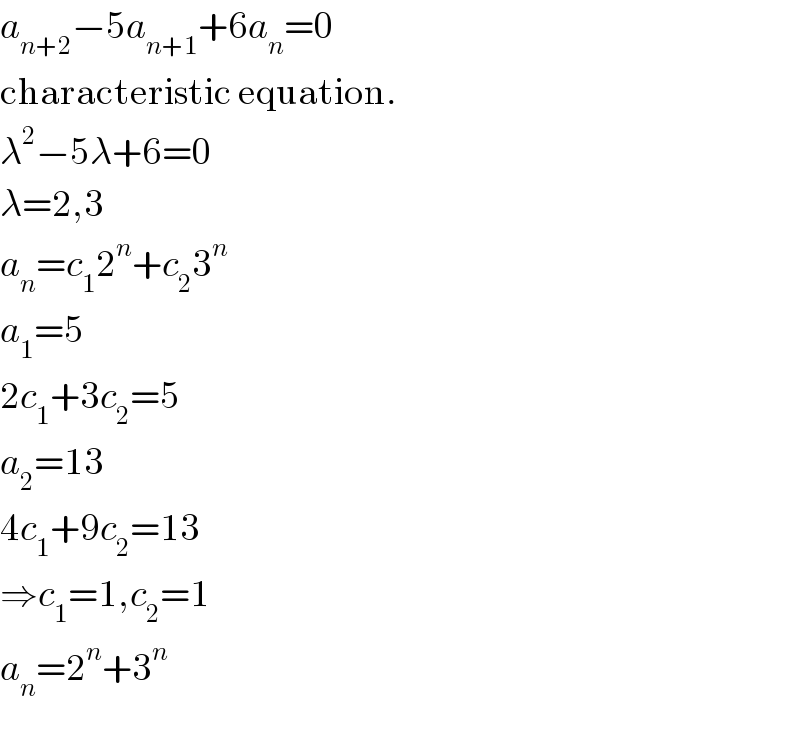
$${a}_{{n}+\mathrm{2}} −\mathrm{5}{a}_{{n}+\mathrm{1}} +\mathrm{6}{a}_{{n}} =\mathrm{0} \\ $$$$\mathrm{characteristic}\:\mathrm{equation}. \\ $$$$\lambda^{\mathrm{2}} −\mathrm{5}\lambda+\mathrm{6}=\mathrm{0} \\ $$$$\lambda=\mathrm{2},\mathrm{3} \\ $$$${a}_{{n}} ={c}_{\mathrm{1}} \mathrm{2}^{{n}} +{c}_{\mathrm{2}} \mathrm{3}^{{n}} \\ $$$${a}_{\mathrm{1}} =\mathrm{5} \\ $$$$\mathrm{2}{c}_{\mathrm{1}} +\mathrm{3}{c}_{\mathrm{2}} =\mathrm{5} \\ $$$${a}_{\mathrm{2}} =\mathrm{13} \\ $$$$\mathrm{4}{c}_{\mathrm{1}} +\mathrm{9}{c}_{\mathrm{2}} =\mathrm{13} \\ $$$$\Rightarrow{c}_{\mathrm{1}} =\mathrm{1},{c}_{\mathrm{2}} =\mathrm{1} \\ $$$${a}_{{n}} =\mathrm{2}^{{n}} +\mathrm{3}^{{n}} \\ $$
Commented by I want to learn more last updated on 08/May/20

$$\mathrm{I}\:\mathrm{appreciate}\:\mathrm{sir}. \\ $$
Commented by I want to learn more last updated on 08/May/20

$$\mathrm{Sir},\:\mathrm{which}\:\mathrm{book}\:\mathrm{can}\:\mathrm{i}\:\mathrm{learn}\:\mathrm{this}. \\ $$
