if-a-1-i-3-find-a-1-5-

Question Number 170675 by MathsFan last updated on 29/May/22

$$\boldsymbol{\mathrm{if}}\:\:\boldsymbol{\mathrm{a}}=−\mathrm{1}−\boldsymbol{{i}}\sqrt{\mathrm{3}} \\ $$$$\:\boldsymbol{\mathrm{find}}\:\boldsymbol{\mathrm{a}}^{\frac{\mathrm{1}}{\mathrm{5}}} \\ $$

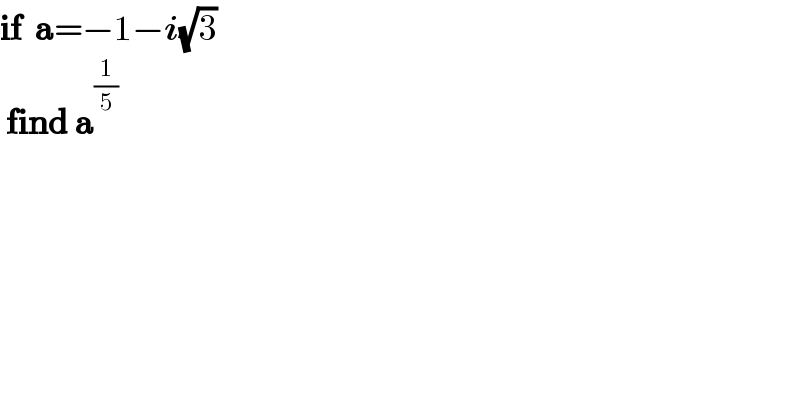
Answered by Mathspace last updated on 29/May/22

∣a∣=(√(1+3))=2 ⇒a=2(−(1/2)−((√3)/2)i) =2 e^(i(((4π)/3))) ⇒a^(1/5) =2^(1/5) e^(i((4π)/(15))) =^5 (√2){cos(((4π)/(15)))+isin(((4π)/(15)))}

$$\mid{a}\mid=\sqrt{\mathrm{1}+\mathrm{3}}=\mathrm{2}\:\Rightarrow{a}=\mathrm{2}\left(−\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{i}\right) \\ $$$$=\mathrm{2}\:{e}^{{i}\left(\frac{\mathrm{4}\pi}{\mathrm{3}}\right)} \:\Rightarrow{a}^{\frac{\mathrm{1}}{\mathrm{5}}} =\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{5}}} \:{e}^{{i}\frac{\mathrm{4}\pi}{\mathrm{15}}} \\ $$$$=^{\mathrm{5}} \sqrt{\mathrm{2}}\left\{{cos}\left(\frac{\mathrm{4}\pi}{\mathrm{15}}\right)+{isin}\left(\frac{\mathrm{4}\pi}{\mathrm{15}}\right)\right\} \\ $$

Commented by MathsFan last updated on 29/May/22

$${thanks} \\ $$

Answered by mr W last updated on 29/May/22

a=2[cos (((4π)/3)+2kπ)+sin (((4π)/3)+2kπ)i] ⇒a^(1/5) =(2)^(1/5) [cos (((4π)/(15))+((2kπ)/5))+sin (((4π)/(15))+((2kπ)/5))i] (k=0,1,2,3,4)

$${a}=\mathrm{2}\left[\mathrm{cos}\:\left(\frac{\mathrm{4}\pi}{\mathrm{3}}+\mathrm{2}{k}\pi\right)+\mathrm{sin}\:\left(\frac{\mathrm{4}\pi}{\mathrm{3}}+\mathrm{2}{k}\pi\right){i}\right] \\ $$$$\Rightarrow{a}^{\frac{\mathrm{1}}{\mathrm{5}}} =\sqrt[{\mathrm{5}}]{\mathrm{2}}\left[\mathrm{cos}\:\left(\frac{\mathrm{4}\pi}{\mathrm{15}}+\frac{\mathrm{2}{k}\pi}{\mathrm{5}}\right)+\mathrm{sin}\:\left(\frac{\mathrm{4}\pi}{\mathrm{15}}+\frac{\mathrm{2}{k}\pi}{\mathrm{5}}\right){i}\right]\: \\ $$$$\left({k}=\mathrm{0},\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4}\right) \\ $$

Commented by MJS_new last updated on 29/May/22

back when I studied mathematics this would have been wrong. it′s a difference between the results of (1) (√4) (2) x^2 =4 because (1) is just a simple calculation but (2) is an equation where we want all possible values of x satisfying the eq. (1) (√4)=2 is unique and not (√4)=±2 (2) x^2 =4 ⇒ x=±2 same for z^(1/5) versus x^5 =z with z=re^(iθ) z^(1/5) =r^(1/5) e^(iθ/5) is unique x^5 =z has the obvious 5 solutions

$$\mathrm{back}\:\mathrm{when}\:\mathrm{I}\:\mathrm{studied}\:\mathrm{mathematics}\:\mathrm{this}\:\mathrm{would} \\ $$$$\mathrm{have}\:\mathrm{been}\:\mathrm{wrong}.\:\mathrm{it}'\mathrm{s}\:\mathrm{a}\:\mathrm{difference}\:\mathrm{between} \\ $$$$\mathrm{the}\:\mathrm{results}\:\mathrm{of} \\ $$$$\left(\mathrm{1}\right)\:\sqrt{\mathrm{4}} \\ $$$$\left(\mathrm{2}\right)\:{x}^{\mathrm{2}} =\mathrm{4} \\ $$$$\mathrm{because}\:\left(\mathrm{1}\right)\:\mathrm{is}\:\mathrm{just}\:\mathrm{a}\:\mathrm{simple}\:\mathrm{calculation}\:\mathrm{but} \\ $$$$\left(\mathrm{2}\right)\:\mathrm{is}\:\mathrm{an}\:\mathrm{equation}\:\mathrm{where}\:\mathrm{we}\:\mathrm{want}\:\mathrm{all}\:\mathrm{possible} \\ $$$$\mathrm{values}\:\mathrm{of}\:{x}\:\mathrm{satisfying}\:\mathrm{the}\:\mathrm{eq}. \\ $$$$\left(\mathrm{1}\right)\:\sqrt{\mathrm{4}}=\mathrm{2}\:\mathrm{is}\:\mathrm{unique}\:\mathrm{and}\:\mathrm{not}\:\sqrt{\mathrm{4}}=\pm\mathrm{2} \\ $$$$\left(\mathrm{2}\right)\:{x}^{\mathrm{2}} =\mathrm{4}\:\Rightarrow\:{x}=\pm\mathrm{2} \\ $$$$\mathrm{same}\:\mathrm{for}\:{z}^{\mathrm{1}/\mathrm{5}} \:\mathrm{versus}\:{x}^{\mathrm{5}} ={z}\:\mathrm{with}\:{z}={r}\mathrm{e}^{\mathrm{i}\theta} \\ $$$${z}^{\mathrm{1}/\mathrm{5}} ={r}^{\mathrm{1}/\mathrm{5}} \mathrm{e}^{\mathrm{i}\theta/\mathrm{5}} \:\mathrm{is}\:\mathrm{unique} \\ $$$${x}^{\mathrm{5}} ={z}\:\mathrm{has}\:\mathrm{the}\:\mathrm{obvious}\:\mathrm{5}\:\mathrm{solutions} \\ $$

Commented by mr W last updated on 30/May/22

basically you are right sir. but i case of complex numbers i think z^(1/5) may have indeed 5 different values. z=re^(iθ) =re^(i(θ+2kπ)) with k∈Z ⇒z^(1/5) =(r)^(1/5) e^(i((θ/5)+((2kπ)/5)))

$${basically}\:{you}\:{are}\:{right}\:{sir}.\:{but}\:{i}\:{case} \\ $$$${of}\:{complex}\:{numbers}\:{i}\:{think}\:{z}^{\frac{\mathrm{1}}{\mathrm{5}}} \:{may} \\ $$$${have}\:{indeed}\:\mathrm{5}\:{different}\:{values}.\: \\ $$$${z}={re}^{{i}\theta} ={re}^{{i}\left(\theta+\mathrm{2}{k}\pi\right)} \:{with}\:{k}\in{Z} \\ $$$$\Rightarrow{z}^{\frac{\mathrm{1}}{\mathrm{5}}} =\sqrt[{\mathrm{5}}]{{r}}\:{e}^{{i}\left(\frac{\theta}{\mathrm{5}}+\frac{\mathrm{2}{k}\pi}{\mathrm{5}}\right)} \\ $$

Facebook Tweet Pin

if-a-1-i-3-find-a-1-5-

Leave a Reply Cancel reply