Question Number 115380 by mathdave last updated on 25/Sep/20
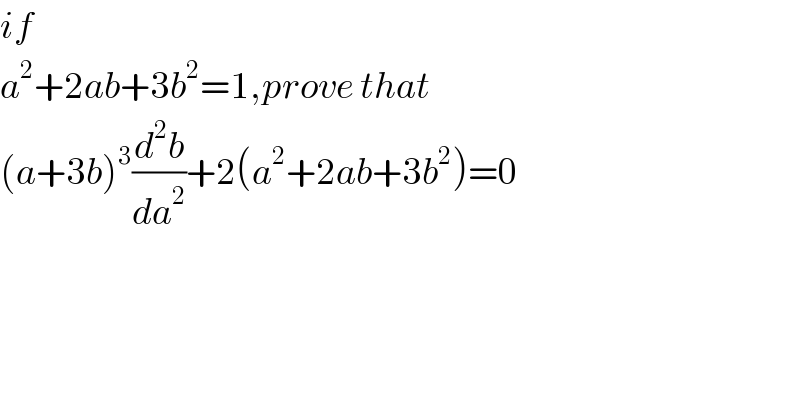
$${if}\: \\ $$$${a}^{\mathrm{2}} +\mathrm{2}{ab}+\mathrm{3}{b}^{\mathrm{2}} =\mathrm{1},{prove}\:{that}\: \\ $$$$\left({a}+\mathrm{3}{b}\right)^{\mathrm{3}} \frac{{d}^{\mathrm{2}} {b}}{{da}^{\mathrm{2}} }+\mathrm{2}\left({a}^{\mathrm{2}} +\mathrm{2}{ab}+\mathrm{3}{b}^{\mathrm{2}} \right)=\mathrm{0} \\ $$
Answered by Dwaipayan Shikari last updated on 25/Sep/20

$$\mathrm{a}^{\mathrm{2}} +\mathrm{2ab}+\mathrm{3b}^{\mathrm{2}} =\mathrm{1} \\ $$$$\mathrm{2a}+\mathrm{2b}+\mathrm{2a}\frac{\mathrm{db}}{\mathrm{da}}+\mathrm{6b}\frac{\mathrm{db}}{\mathrm{da}}=\mathrm{0} \\ $$$$\frac{\mathrm{db}}{\mathrm{da}}=−\frac{\mathrm{a}+\mathrm{b}}{\mathrm{a}+\mathrm{3b}}\rightarrow\left(\mathrm{a}\right) \\ $$$$\mathrm{2}+\mathrm{2}\frac{\mathrm{db}}{\mathrm{da}}+\mathrm{2a}\frac{\mathrm{d}^{\mathrm{2}} \mathrm{b}}{\mathrm{da}^{\mathrm{2}} }+\mathrm{2}\frac{\mathrm{db}}{\mathrm{da}}+\mathrm{6b}\frac{\mathrm{d}^{\mathrm{2}} \mathrm{b}}{\mathrm{da}^{\mathrm{2}} }+\mathrm{6}\left(\frac{\mathrm{db}}{\mathrm{da}}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{2}+\mathrm{4}\frac{\mathrm{db}}{\mathrm{da}}+\mathrm{2}\left(\mathrm{a}+\mathrm{3b}\right)\frac{\mathrm{d}^{\mathrm{2}} \mathrm{b}}{\mathrm{da}^{\mathrm{2}} }+\mathrm{6}\left(\frac{\mathrm{db}}{\mathrm{da}}\right)=\mathrm{0} \\ $$$$\mathrm{1}−\frac{\mathrm{2a}+\mathrm{2b}}{\mathrm{a}+\mathrm{3b}}+\left(\mathrm{a}+\mathrm{3b}\right).\frac{\mathrm{d}^{\mathrm{2}} \mathrm{b}}{\mathrm{da}^{\mathrm{2}} }+\mathrm{3}\left(\frac{\mathrm{a}+\mathrm{b}}{\mathrm{a}+\mathrm{3b}}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\frac{\mathrm{d}^{\mathrm{2}} \mathrm{b}}{\mathrm{da}^{\mathrm{2}} }\left(\mathrm{a}+\mathrm{3b}\right)=−\mathrm{3}\left(\frac{\mathrm{a}+\mathrm{b}}{\mathrm{a}+\mathrm{3b}}\right)^{\mathrm{2}} +\frac{\mathrm{2}\left(\mathrm{a}+\mathrm{b}\right)}{\mathrm{a}+\mathrm{3b}}−\mathrm{1} \\ $$$$\frac{\mathrm{d}^{\mathrm{2}} \mathrm{b}}{\mathrm{da}^{\mathrm{2}} }\left(\mathrm{a}+\mathrm{3b}\right)^{\mathrm{3}} =−\mathrm{3a}^{\mathrm{2}} −\mathrm{6ab}−\mathrm{3b}^{\mathrm{2}} +\mathrm{2}\left(\mathrm{a}+\mathrm{3b}\right)\left(\mathrm{a}+\mathrm{b}\right)−\mathrm{a}^{\mathrm{2}} −\mathrm{6ab}−\mathrm{9b}^{\mathrm{2}} \\ $$$$\frac{\mathrm{d}^{\mathrm{2}} \mathrm{b}}{\mathrm{da}^{\mathrm{2}} }\left(\mathrm{a}+\mathrm{3b}\right)^{\mathrm{3}} =−\mathrm{4a}^{\mathrm{2}} −\mathrm{12ab}−\mathrm{12b}^{\mathrm{2}} +\mathrm{2a}^{\mathrm{2}} +\mathrm{6ab}+\mathrm{2ab}+\mathrm{6b}^{\mathrm{2}} \\ $$$$\frac{\mathrm{d}^{\mathrm{2}} \mathrm{b}}{\mathrm{da}^{\mathrm{2}} }\left(\mathrm{a}+\mathrm{3b}\right)^{\mathrm{3}} =−\mathrm{2}\left(\mathrm{a}^{\mathrm{2}} +\mathrm{2ab}+\mathrm{3b}^{\mathrm{2}} \right) \\ $$$$\frac{\mathrm{d}^{\mathrm{2}} \mathrm{b}}{\mathrm{da}^{\mathrm{2}} }\left(\mathrm{a}+\mathrm{3b}\right)^{\mathrm{3}} +\mathrm{2}\left(\mathrm{a}^{\mathrm{2}} +\mathrm{2ab}+\mathrm{3b}^{\mathrm{2}} \right)=\mathrm{0} \\ $$
Answered by 1549442205PVT last updated on 25/Sep/20

$${a}^{\mathrm{2}} +\mathrm{2}{ab}+\mathrm{3}{b}^{\mathrm{2}} =\mathrm{1}\Leftrightarrow\mathrm{3b}^{\mathrm{2}} +\mathrm{2ab}+\mathrm{a}^{\mathrm{2}} −\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{this}\:\mathrm{is}\:\mathrm{quadratic}\:\mathrm{eqn}.\mathrm{w}.\mathrm{r}.\mathrm{t}\:\mathrm{b}\:\mathrm{with} \\ $$$$\Delta'=\mathrm{a}^{\mathrm{2}} −\mathrm{3a}^{\mathrm{2}} +\mathrm{3}=\mathrm{3}−\mathrm{2a}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{b}=\frac{−\mathrm{a}\pm\sqrt{\mathrm{3}−\mathrm{2a}^{\mathrm{2}} }}{\mathrm{3}}\left(\mathrm{1}\right) \\ $$$$\Rightarrow\frac{\mathrm{db}}{\mathrm{da}}=\left(−\mathrm{1}\mp\frac{\mathrm{2a}}{\:\sqrt{\mathrm{3}−\mathrm{2a}^{\mathrm{2}} }}\right)/\mathrm{3} \\ $$$$\Rightarrow\frac{\mathrm{d}^{\mathrm{2}} \mathrm{b}}{\mathrm{da}^{\mathrm{2}} }=\mp\left(\frac{\mathrm{2}\sqrt{\mathrm{3}−\mathrm{2a}^{\mathrm{2}} }+\frac{\mathrm{4a}^{\mathrm{2}} }{\:\sqrt{\mathrm{3}−\mathrm{2a}^{\mathrm{2}} }}}{\mathrm{3}\left(\mathrm{3}−\mathrm{2a}^{\mathrm{2}} \right)}\right) \\ $$$$=\mp\left(\frac{\mathrm{2}}{\left(\mathrm{3}−\mathrm{2a}^{\mathrm{2}} \right)\sqrt{\mathrm{3}−\mathrm{2a}^{\mathrm{2}} }}\right)\left(\mathrm{2}\right) \\ $$$$\mathrm{From}\left(\mathrm{1}\right)\mathrm{we}\:\mathrm{have}\:\mathrm{3b}+\mathrm{a}=\pm\sqrt{\mathrm{3}−\mathrm{2a}^{\mathrm{2}} } \\ $$$$\Rightarrow\left(\mathrm{3b}+\mathrm{a}\right)^{\mathrm{3}} =\pm\left(\mathrm{3}−\mathrm{2a}^{\mathrm{2}} \right)\sqrt{\mathrm{3}−\mathrm{2a}^{\mathrm{2}} }\left(\mathrm{3}\right) \\ $$$$\mathrm{From}\left(\mathrm{2}\right)\left(\mathrm{3}\right)\mathrm{we}\:\mathrm{get} \\ $$$$\left(\mathrm{3b}+\mathrm{a}\right)^{\mathrm{3}} \frac{\mathrm{d}^{\mathrm{2}} \mathrm{b}}{\mathrm{da}^{\mathrm{2}} }=−\mathrm{2} \\ $$$$\Rightarrow\left(\mathrm{3b}+\mathrm{a}\right)^{\mathrm{3}} \frac{\mathrm{d}^{\mathrm{2}} \mathrm{b}}{\mathrm{da}^{\mathrm{2}} }+\mathrm{2}\left(\mathrm{a}^{\mathrm{2}} +\mathrm{2ab}+\mathrm{3b}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\left(\boldsymbol{\mathrm{Q}}.\boldsymbol{\mathrm{E}}.\boldsymbol{\mathrm{D}}\right) \\ $$
