Question Number 104486 by Anindita last updated on 21/Jul/20
![If A = [(3,(−4),2),((−2),1,0),((−1),(−1),1) ]and B = [(1,2,(−2)),(2,5,(−4)),(3,7,(−5)) ]then show that AB = BA = I_3 .](https://www.tinkutara.com/question/Q104486.png)
$$\boldsymbol{\mathrm{If}}\:\boldsymbol{\mathrm{A}}\:=\:\begin{bmatrix}{\mathrm{3}}&{−\mathrm{4}}&{\mathrm{2}}\\{−\mathrm{2}}&{\mathrm{1}}&{\mathrm{0}}\\{−\mathrm{1}}&{−\mathrm{1}}&{\mathrm{1}}\end{bmatrix}\boldsymbol{\mathrm{and}}\: \\ $$$$\boldsymbol{\mathrm{B}}\:=\:\begin{bmatrix}{\mathrm{1}}&{\mathrm{2}}&{−\mathrm{2}}\\{\mathrm{2}}&{\mathrm{5}}&{−\mathrm{4}}\\{\mathrm{3}}&{\mathrm{7}}&{−\mathrm{5}}\end{bmatrix}\boldsymbol{\mathrm{then}}\: \\ $$$$\boldsymbol{\mathrm{show}}\:\boldsymbol{\mathrm{that}}\:\boldsymbol{\mathrm{AB}}\:=\:\boldsymbol{\mathrm{BA}}\:=\:\boldsymbol{\mathrm{I}}_{\mathrm{3}} \:. \\ $$
Answered by OlafThorendsen last updated on 21/Jul/20
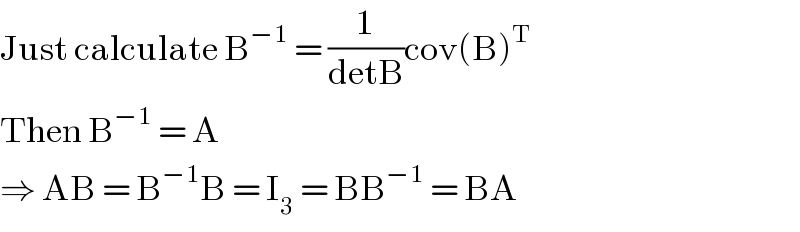
$$\mathrm{Just}\:\mathrm{calculate}\:\mathrm{B}^{−\mathrm{1}} \:=\:\frac{\mathrm{1}}{\mathrm{detB}}\mathrm{cov}\left(\mathrm{B}\right)^{\mathrm{T}} \\ $$$$\mathrm{Then}\:\mathrm{B}^{−\mathrm{1}} \:=\:\mathrm{A} \\ $$$$\Rightarrow\:\mathrm{AB}\:=\:\mathrm{B}^{−\mathrm{1}} \mathrm{B}\:=\:\mathrm{I}_{\mathrm{3}} \:=\:\mathrm{BB}^{−\mathrm{1}} \:=\:\mathrm{BA} \\ $$
