Question Number 25184 by lucky singh last updated on 05/Dec/17

$${if}\:{a}\:{and}\:{b}\:{are}\:{the}\:{root}\:{of}\:{the}\:{quadratic}\:{equation}\:{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{3}\:{then}\:{find}\:{the}\:{value}\:{of}\:\alpha^{\mathrm{2}} /\beta+\beta^{\mathrm{2}} /\alpha \\ $$
Commented by prakash jain last updated on 05/Dec/17
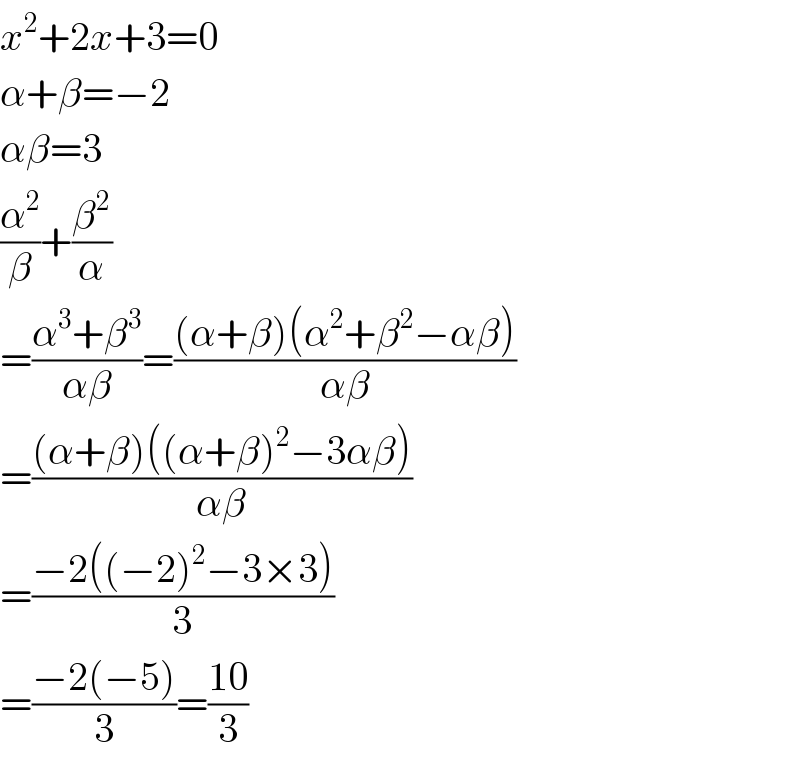
$${x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{3}=\mathrm{0} \\ $$$$\alpha+\beta=−\mathrm{2} \\ $$$$\alpha\beta=\mathrm{3} \\ $$$$\frac{\alpha^{\mathrm{2}} }{\beta}+\frac{\beta^{\mathrm{2}} }{\alpha} \\ $$$$=\frac{\alpha^{\mathrm{3}} +\beta^{\mathrm{3}} }{\alpha\beta}=\frac{\left(\alpha+\beta\right)\left(\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} −\alpha\beta\right)}{\alpha\beta} \\ $$$$=\frac{\left(\alpha+\beta\right)\left(\left(\alpha+\beta\right)^{\mathrm{2}} −\mathrm{3}\alpha\beta\right)}{\alpha\beta} \\ $$$$=\frac{−\mathrm{2}\left(\left(−\mathrm{2}\right)^{\mathrm{2}} −\mathrm{3}×\mathrm{3}\right)}{\mathrm{3}} \\ $$$$=\frac{−\mathrm{2}\left(−\mathrm{5}\right)}{\mathrm{3}}=\frac{\mathrm{10}}{\mathrm{3}} \\ $$
Answered by ibraheem160 last updated on 06/Dec/17
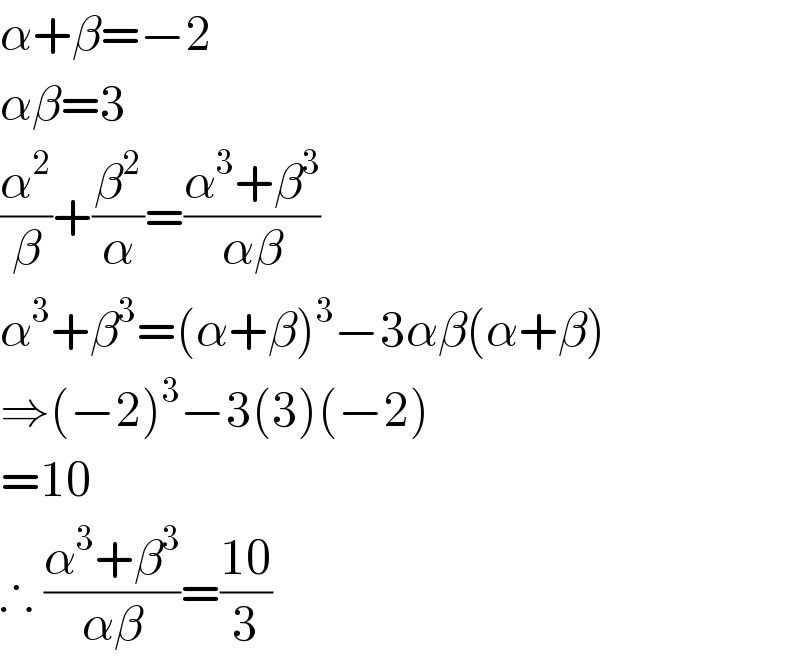
$$\alpha+\beta=−\mathrm{2} \\ $$$$\alpha\beta=\mathrm{3} \\ $$$$\frac{\alpha^{\mathrm{2}} }{\beta}+\frac{\beta^{\mathrm{2}} }{\alpha}=\frac{\alpha^{\mathrm{3}} +\beta^{\mathrm{3}} }{\alpha\beta} \\ $$$$\alpha^{\mathrm{3}} +\beta^{\mathrm{3}} =\left(\alpha+\beta\right)^{\mathrm{3}} −\mathrm{3}\alpha\beta\left(\alpha+\beta\right) \\ $$$$\Rightarrow\left(−\mathrm{2}\right)^{\mathrm{3}} −\mathrm{3}\left(\mathrm{3}\right)\left(−\mathrm{2}\right) \\ $$$$=\mathrm{10} \\ $$$$\therefore\:\frac{\alpha^{\mathrm{3}} +\beta^{\mathrm{3}} }{\alpha\beta}=\frac{\mathrm{10}}{\mathrm{3}} \\ $$
