If-A-and-B-are-two-points-on-a-circle-of-radius-r-then-prove-that-mAB-2r-

Question Number 25344 by Rasheed.Sindhi last updated on 08/Dec/17

If A and B are two points on a

circle of radius r, then prove that

m \overset{―}{AB} ⩽ 2 r .

Answered by jota+ last updated on 08/Dec/17

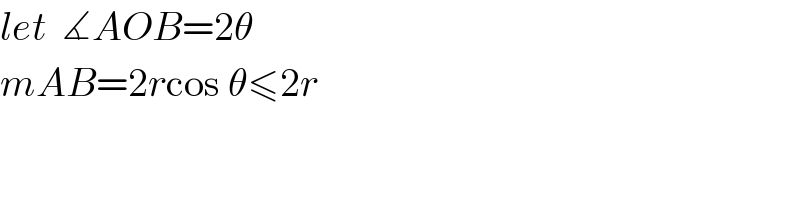
l e t ∡ A O B = 2 θ

m A B = 2 r \cos θ ⩽ 2 r

Commented by Rasheed.Sindhi last updated on 08/Dec/17

T h^{α} n k U!