Question Number 27820 by bmind4860 last updated on 15/Jan/18
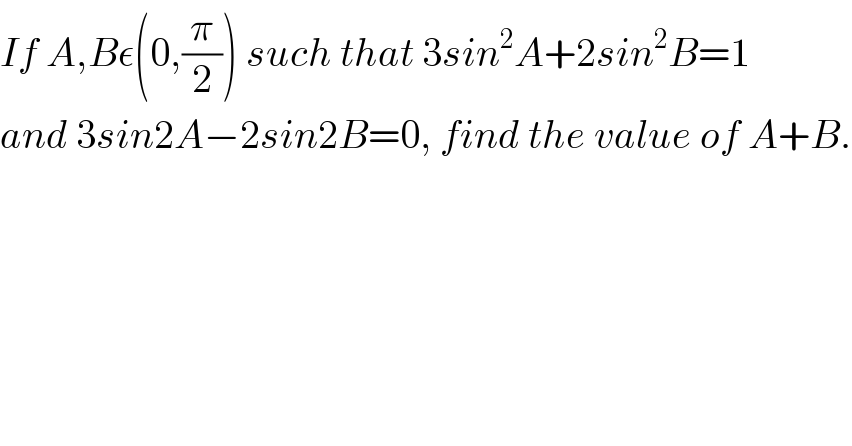
$${If}\:{A},{B}\epsilon\left(\mathrm{0},\frac{\pi}{\mathrm{2}}\right)\:{such}\:{that}\:\mathrm{3}{sin}^{\mathrm{2}} {A}+\mathrm{2}{sin}^{\mathrm{2}} {B}=\mathrm{1} \\ $$$${and}\:\mathrm{3}{sin}\mathrm{2}{A}−\mathrm{2}{sin}\mathrm{2}{B}=\mathrm{0},\:{find}\:{the}\:{value}\:{of}\:{A}+{B}. \\ $$
Answered by ajfour last updated on 15/Jan/18

$$\frac{\mathrm{3}}{\mathrm{2}}\left(\mathrm{1}−\mathrm{cos}\:\mathrm{2}{A}\right)+\mathrm{1}−\mathrm{cos}\:\mathrm{2}{B}=\mathrm{1} \\ $$$$\Rightarrow\:\mathrm{3cos}\:\mathrm{2}{A}+\mathrm{2cos}\:\mathrm{2}{B}=\mathrm{3}\:\:\:….\left({i}\right) \\ $$$${and}\:\:{since}\:\:\mathrm{3sin}\:\mathrm{2}{A}=\mathrm{2sin}\:\mathrm{2}{B} \\ $$$$\mathrm{9sin}\:^{\mathrm{2}} \mathrm{2}{A}=\mathrm{4sin}\:^{\mathrm{2}} \mathrm{2}{B} \\ $$$$\Rightarrow\:\:\mathrm{9}−\mathrm{9cos}\:^{\mathrm{2}} \mathrm{2}{A}=\mathrm{4}−\mathrm{4cos}\:^{\mathrm{2}} \mathrm{2}{B} \\ $$$$\Rightarrow\:\mathrm{9cos}\:^{\mathrm{2}} \mathrm{2}{A}−\mathrm{4cos}\:^{\mathrm{2}} \mathrm{2}{B}=\mathrm{5} \\ $$$${or}\:\:\left(\mathrm{3cos}\:\mathrm{2}{A}−\mathrm{2cos}\:\mathrm{2}{B}\right)\left(\mathrm{3cos}\:\mathrm{2}{A}+\mathrm{2cos}\:\mathrm{2}{B}\right)=\mathrm{5} \\ $$$${using}\:\left({i}\right): \\ $$$$\mathrm{3cos}\:\mathrm{2}{A}−\mathrm{2cos}\:\mathrm{2}{B}=\frac{\mathrm{5}}{\mathrm{3}} \\ $$$${and}\:{as}\:\:\:\mathrm{3cos}\:\mathrm{2}{A}+\mathrm{2cos}\:\mathrm{2}{B}=\mathrm{3} \\ $$$${adding}\:{the}\:{above}\:{two}\:{eqs}. \\ $$$$\mathrm{6cos}\:\mathrm{2}{A}=\frac{\mathrm{14}}{\mathrm{3}}\:\:\Rightarrow\:\:\mathrm{cos}\:\mathrm{2}{A}=\frac{\mathrm{7}}{\mathrm{9}} \\ $$$$\:\:\:\:\:{and}\:\:\mathrm{sin}\:\mathrm{2}{A}=\sqrt{\mathrm{1}−\frac{\mathrm{49}}{\mathrm{81}}}\:=\frac{\mathrm{4}\sqrt{\mathrm{2}}}{\mathrm{9}} \\ $$$${subtracting}\:{them}, \\ $$$$\mathrm{4cos}\:\mathrm{2}{B}=\frac{\mathrm{4}}{\mathrm{3}}\:\:\Rightarrow\:\:\:\mathrm{cos}\:\mathrm{2}{B}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\:\:\:\:{and}\:\:\mathrm{sin}\:\mathrm{2}{B}=\sqrt{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{9}}}\:=\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{3}} \\ $$$$\mathrm{cos}\:\left(\mathrm{2}{A}+\mathrm{2}{B}\right)=\mathrm{cos}\:\mathrm{2}{A}\mathrm{cos}\:\mathrm{2}{B} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{sin}\:\mathrm{2}{A}\mathrm{sin}\:\mathrm{2}{B} \\ $$$$\:\:\:\:\:=\frac{\mathrm{7}}{\mathrm{9}}×\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{4}\sqrt{\mathrm{2}}}{\mathrm{9}}×\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{3}} \\ $$$$\:\:\:=−\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\mathrm{cos}\:\left({A}+{B}\right)=\sqrt{\frac{\mathrm{1}+\mathrm{cos}\:\left(\mathrm{2}{A}+\mathrm{2}{B}\right)}{\mathrm{2}}} \\ $$$$\:\:\:\:\:\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}} \\ $$$${A}+{B}=\mathrm{cos}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right). \\ $$
Commented by bmind4860 last updated on 15/Jan/18

$${perfect} \\ $$
