Question Number 104452 by Anindita last updated on 21/Jul/20
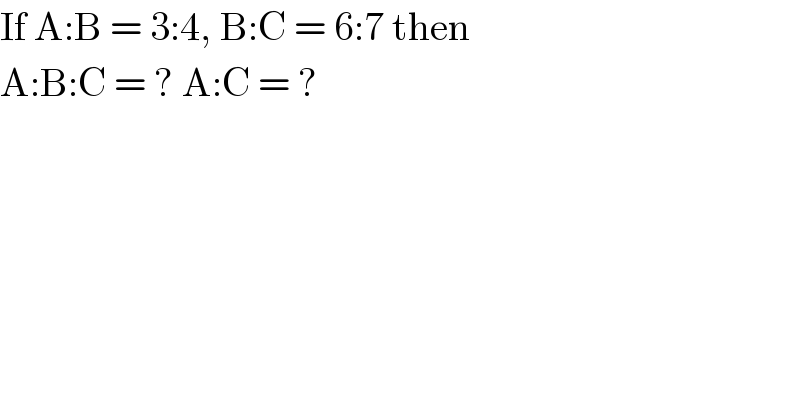
$$\mathrm{If}\:\mathrm{A}:\mathrm{B}\:=\:\mathrm{3}:\mathrm{4},\:\mathrm{B}:\mathrm{C}\:=\:\mathrm{6}:\mathrm{7}\:\mathrm{then} \\ $$$$\mathrm{A}:\mathrm{B}:\mathrm{C}\:=\:?\:\mathrm{A}:\mathrm{C}\:=\:?\: \\ $$
Answered by bemath last updated on 21/Jul/20

$${A}\::\:{B}\::\:{C}\:=\:\mathrm{9}\::\:\mathrm{12}\::\:\mathrm{14} \\ $$
Answered by Rasheed.Sindhi last updated on 22/Jul/20

$$\begin{vmatrix}{\:\:\mathrm{A}}&{\:\:\::}&{\:\:\:\:\:\:\:\:\:\mathrm{B}}&{:}&{\:\:\mathrm{C}}\\{\:\:\mathrm{3}}&{\:\:\::}&{\:\:\:\:\:\:\:\:\:\mathrm{4}}&{}&{}\\{}&{}&{\:\:\:\:\:\:\:\:\:\mathrm{6}}&{:}&{\:\:\:\mathrm{7}}\\{−−}&{−}&{−−−−}&{−}&{−−}\\{\mathrm{3}×\underset{−} {\mathrm{3}}}&{}&{\:\:\:\mathrm{4}×\underset{−} {\mathrm{3}}}&{}&{}\\{}&{}&{=\mathrm{6}×\underset{−} {\mathrm{2}}}&{}&{\mathrm{7}×\underset{−} {\mathrm{2}}}\\{−−}&{−}&{−−−−}&{−}&{−−}\\{\mathrm{9}}&{\:\::}&{\underset{{lcm}\:{of}\:\mathrm{4}\:\&\:\mathrm{6}} {\mathrm{12}}}&{\:\::}&{\:\:\:\:\:\mathrm{14}}\end{vmatrix} \\ $$$$\mathrm{A}:\mathrm{C}=\mathrm{9}:\mathrm{14} \\ $$
Commented by harckinwunmy last updated on 21/Jul/20

$$\mathrm{can}\:\mathrm{u}\:\mathrm{pls}\:\mathrm{explain} \\ $$
Commented by Rasheed.Sindhi last updated on 22/Jul/20
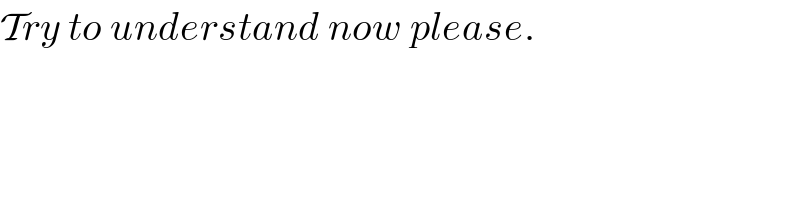
$$\mathcal{T}{ry}\:{to}\:{understand}\:{now}\:{please}. \\ $$
Answered by 1549442205PVT last updated on 22/Jul/20
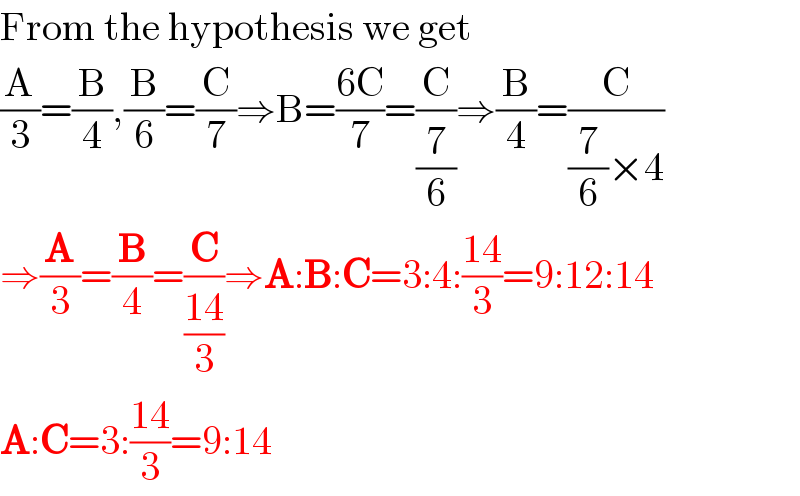
$$\mathrm{From}\:\mathrm{the}\:\mathrm{hypothesis}\:\mathrm{we}\:\mathrm{get} \\ $$$$\frac{\mathrm{A}}{\mathrm{3}}=\frac{\mathrm{B}}{\mathrm{4}},\frac{\mathrm{B}}{\mathrm{6}}=\frac{\mathrm{C}}{\mathrm{7}}\Rightarrow\mathrm{B}=\frac{\mathrm{6C}}{\mathrm{7}}=\frac{\mathrm{C}}{\frac{\mathrm{7}}{\mathrm{6}}}\Rightarrow\frac{\mathrm{B}}{\mathrm{4}}=\frac{\mathrm{C}}{\frac{\mathrm{7}}{\mathrm{6}}×\mathrm{4}} \\ $$$$\Rightarrow\frac{\boldsymbol{\mathrm{A}}}{\mathrm{3}}=\frac{\boldsymbol{\mathrm{B}}}{\mathrm{4}}=\frac{\boldsymbol{\mathrm{C}}}{\frac{\mathrm{14}}{\mathrm{3}}}\Rightarrow\boldsymbol{\mathrm{A}}:\boldsymbol{\mathrm{B}}:\boldsymbol{\mathrm{C}}=\mathrm{3}:\mathrm{4}:\frac{\mathrm{14}}{\mathrm{3}}=\mathrm{9}:\mathrm{12}:\mathrm{14} \\ $$$$\boldsymbol{\mathrm{A}}:\boldsymbol{\mathrm{C}}=\mathrm{3}:\frac{\mathrm{14}}{\mathrm{3}}=\mathrm{9}:\mathrm{14} \\ $$
