Menu Close

If-a-b-a-b-13-Find-2a-b-

Tinku Tara 0 Comments
Pin




Question Number 176037 by Shrinava last updated on 11/Sep/22
If (a−b)(a + b) = 13 Find 2a + b = ?
If(a−b)(a+b)=13Find2a+b=?
Commented by Rasheed.Sindhi last updated on 11/Sep/22
20
20
Answered by Rasheed.Sindhi last updated on 11/Sep/22
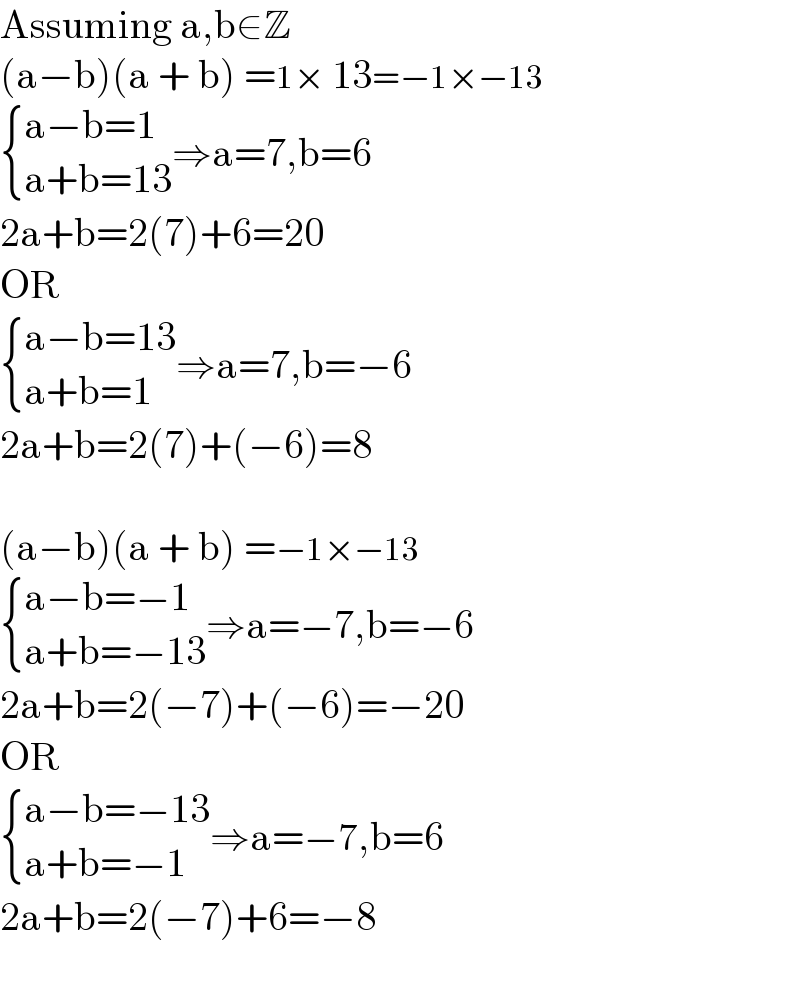
Assuming a,b∈Z (a−b)(a + b) =1× 13=−1×−13 { ((a−b=1)),((a+b=13)) :}⇒a=7,b=6 2a+b=2(7)+6=20 OR { ((a−b=13)),((a+b=1)) :}⇒a=7,b=−6 2a+b=2(7)+(−6)=8 (a−b)(a + b) =−1×−13 { ((a−b=−1)),((a+b=−13)) :}⇒a=−7,b=−6 2a+b=2(−7)+(−6)=−20 OR { ((a−b=−13)),((a+b=−1)) :}⇒a=−7,b=6 2a+b=2(−7)+6=−8
Assuminga,b∈Z(a−b)(a+b)=1×13=−1×−13{a−b=1a+b=13⇒a=7,b=62a+b=2(7)+6=20OR{a−b=13a+b=1⇒a=7,b=−62a+b=2(7)+(−6)=8(a−b)(a+b)=−1×−13{a−b=−1a+b=−13⇒a=−7,b=−62a+b=2(−7)+(−6)=−20OR{a−b=−13a+b=−1⇒a=−7,b=62a+b=2(−7)+6=−8
Commented by Shrinava last updated on 11/Sep/22
a,b∈N
a,b∈N
Commented by Rasheed.Sindhi last updated on 11/Sep/22
If a,b∈N: 2a+b=2(7)+6=20
Ifa,b∈N:2a+b=2(7)+6=20
Commented by Shrinava last updated on 11/Sep/22
cool thank you dear ser
coolthankyoudearser
Answered by BaliramKumar last updated on 11/Sep/22
a, b ∈ N (a−b)(a+b) = 1×13 a−b = 1 a+b = 13 a = 7, b = 6 2a+b = 2∙7 + 6 = 14 + 6 = 20 Answer ••▶ a, b ∈ Z (a, b) = (7, 6), (−7, −6), (7, −6), (−7, 6) 2a + b = 20, −20, 8, −8 Answers ••▶ a, b ∈ R ∞ solutions
a,b∈N(a−b)(a+b)=1×13a−b=1a+b=13a=7,b=62a+b=2⋅7+6=14+6=20Answer∙∙▸a,b∈Z(a,b)=(7,6),(−7,−6),(7,−6),(−7,6)2a+b=20,−20,8,−8Answers∙∙▸a,b∈R∞solutions
Commented by Shrinava last updated on 11/Sep/22
thank you dear ser
thankyoudearser

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *