Question Number 181138 by Agnibhoo98 last updated on 22/Nov/22
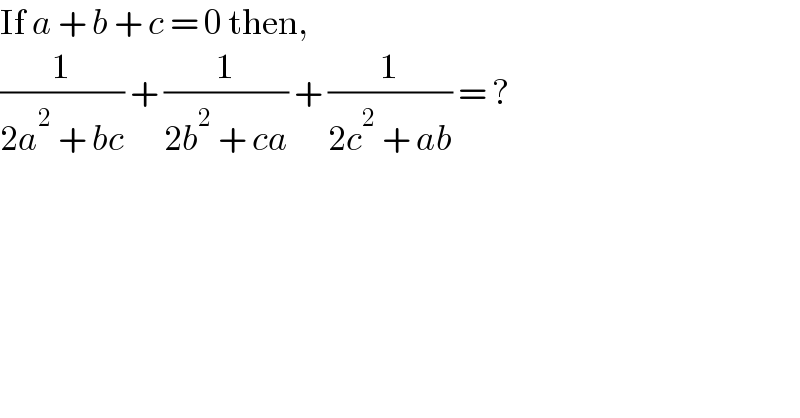
$$\mathrm{If}\:{a}\:+\:{b}\:+\:{c}\:=\:\mathrm{0}\:\mathrm{then}, \\ $$$$\frac{\mathrm{1}}{\mathrm{2}{a}^{\mathrm{2}} \:+\:{bc}}\:+\:\frac{\mathrm{1}}{\mathrm{2}{b}^{\mathrm{2}} \:+\:{ca}}\:+\:\frac{\mathrm{1}}{\mathrm{2}{c}^{\mathrm{2}} \:+\:{ab}}\:=\:? \\ $$
Answered by som(math1967) last updated on 22/Nov/22
![a+b+c=0 ⇒a^2 =−ab−ca b^2 =−ab−bc c^2 =−ca−bc 2a^2 +bc=a^2 −ab−ca+bc=(a−b)(a−c) 2b^2 +ca=(b−c)(b−a) 2c^2 +ab=(c−a)(c−b) (1/(2a^2 + bc)) + (1/(2b^2 + ca)) + (1/(2c^2 + ab)) =(1/((a−b)(a−c)))+(1/((b−c)(b−a)))+(1/((c−a)(c−b))) =−(1/((a−b)(c−a)))−(1/((b−c)(a−b)))−(1/((c−a)(b−c))) =−[((b−c+c−a+a−b)/((a−b)(b−c)(c−a)))]=0](https://www.tinkutara.com/question/Q181139.png)
$$\:{a}+{b}+{c}=\mathrm{0} \\ $$$$\Rightarrow{a}^{\mathrm{2}} =−{ab}−{ca} \\ $$$${b}^{\mathrm{2}} =−{ab}−{bc} \\ $$$${c}^{\mathrm{2}} =−{ca}−{bc} \\ $$$$\mathrm{2}{a}^{\mathrm{2}} +{bc}={a}^{\mathrm{2}} −{ab}−{ca}+{bc}=\left({a}−{b}\right)\left({a}−{c}\right) \\ $$$$\mathrm{2}{b}^{\mathrm{2}} +{ca}=\left({b}−{c}\right)\left({b}−{a}\right) \\ $$$$\mathrm{2}{c}^{\mathrm{2}} +{ab}=\left({c}−{a}\right)\left({c}−{b}\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{2}{a}^{\mathrm{2}} \:+\:{bc}}\:+\:\frac{\mathrm{1}}{\mathrm{2}{b}^{\mathrm{2}} \:+\:{ca}}\:+\:\frac{\mathrm{1}}{\mathrm{2}{c}^{\mathrm{2}} \:+\:{ab}} \\ $$$$=\frac{\mathrm{1}}{\left({a}−{b}\right)\left({a}−{c}\right)}+\frac{\mathrm{1}}{\left({b}−{c}\right)\left({b}−{a}\right)}+\frac{\mathrm{1}}{\left({c}−{a}\right)\left({c}−{b}\right)} \\ $$$$=−\frac{\mathrm{1}}{\left({a}−{b}\right)\left({c}−{a}\right)}−\frac{\mathrm{1}}{\left({b}−{c}\right)\left({a}−{b}\right)}−\frac{\mathrm{1}}{\left({c}−{a}\right)\left({b}−{c}\right)} \\ $$$$=−\left[\frac{{b}−{c}+{c}−{a}+{a}−{b}}{\left({a}−{b}\right)\left({b}−{c}\right)\left({c}−{a}\right)}\right]=\mathrm{0} \\ $$
