Question Number 53391 by Kunal12588 last updated on 21/Jan/19
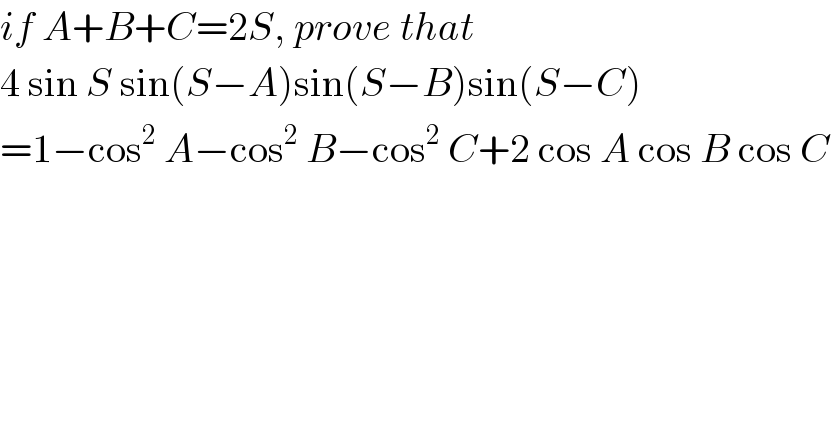
$${if}\:{A}+{B}+{C}=\mathrm{2}{S},\:{prove}\:{that}\: \\ $$$$\mathrm{4}\:\mathrm{sin}\:{S}\:\mathrm{sin}\left({S}−{A}\right)\mathrm{sin}\left({S}−{B}\right)\mathrm{sin}\left({S}−{C}\right) \\ $$$$=\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \:{A}−\mathrm{cos}^{\mathrm{2}} \:{B}−\mathrm{cos}^{\mathrm{2}} \:{C}+\mathrm{2}\:\mathrm{cos}\:{A}\:\mathrm{cos}\:{B}\:\mathrm{cos}\:{C}\: \\ $$
Commented by Kunal12588 last updated on 21/Jan/19
![4s_s s_(s−a) s_(s−b) s_(s−c) =[2s_s s_(s−a) ][2s_(s−b) s_(s−c) ] =(c_(s−s+a) −c_(s+s−a) )(c_(s−b−s+c) −c_(s−b+s−c) ) =(c_a −c_(2s−a) )(c_(b−c) −c_(s−b−c) ) =(c_a −c_(a+b+c−a) )(c_(b−c) −c_(a+b+c−b−c) ) =(c_a −c_(b+c) )(c_(b−c) −c_a ) =−c_a ^2 −c_(b+c) c_(b−c) +c_a c_(b−c) +c_a c_(b+c) =−c_a ^2 −(1/2)(c_(b+c+b−c) −c_(b+c−b+c) )+c_a (c_(b−c) +c_(b+c) ) =−c_a ^2 −(1/2)(c_(2b) −c_(2c) )+c_a (2c_((b−c+b+c)/2) c_((b+c−b+c)/2) ) =−c_a ^2 −(1/2)(2c_b ^2 −2c_c ^2 +2)+2c_a c_b c_c =1−c_a ^2 −c_b ^2 −c_c ^2 +2c_a c_b c_c](https://www.tinkutara.com/question/Q53392.png)
$$\mathrm{4}{s}_{{s}} {s}_{{s}−{a}} {s}_{{s}−{b}} {s}_{{s}−{c}} \\ $$$$=\left[\mathrm{2}{s}_{{s}} {s}_{{s}−{a}} \right]\left[\mathrm{2}{s}_{{s}−{b}} {s}_{{s}−{c}} \right] \\ $$$$=\left({c}_{{s}−{s}+{a}} −{c}_{{s}+{s}−{a}} \right)\left({c}_{{s}−{b}−{s}+{c}} −{c}_{{s}−{b}+{s}−{c}} \right) \\ $$$$=\left({c}_{{a}} −{c}_{\mathrm{2}{s}−{a}} \right)\left({c}_{{b}−{c}} −{c}_{{s}−{b}−{c}} \right) \\ $$$$=\left({c}_{{a}} −{c}_{{a}+{b}+{c}−{a}} \right)\left({c}_{{b}−{c}} −{c}_{{a}+{b}+{c}−{b}−{c}} \right) \\ $$$$=\left({c}_{{a}} −{c}_{{b}+{c}} \right)\left({c}_{{b}−{c}} −{c}_{{a}} \right) \\ $$$$=−{c}_{{a}} ^{\mathrm{2}} −{c}_{{b}+{c}} {c}_{{b}−{c}} +{c}_{{a}} {c}_{{b}−{c}} +{c}_{{a}} {c}_{{b}+{c}} \\ $$$$=−{c}_{{a}} ^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}}\left({c}_{{b}+{c}+{b}−{c}} −{c}_{{b}+{c}−{b}+{c}} \right)+{c}_{{a}} \left({c}_{{b}−{c}} +{c}_{{b}+{c}} \right) \\ $$$$=−{c}_{{a}} ^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}}\left({c}_{\mathrm{2}{b}} −{c}_{\mathrm{2}{c}} \right)+{c}_{{a}} \left(\mathrm{2}{c}_{\left({b}−{c}+{b}+{c}\right)/\mathrm{2}} {c}_{\left({b}+{c}−{b}+{c}\right)/\mathrm{2}} \right) \\ $$$$=−{c}_{{a}} ^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}{c}_{{b}} ^{\mathrm{2}} −\mathrm{2}{c}_{{c}} ^{\mathrm{2}} +\mathrm{2}\right)+\mathrm{2}{c}_{{a}} {c}_{{b}} {c}_{{c}} \\ $$$$=\mathrm{1}−{c}_{{a}} ^{\mathrm{2}} −{c}_{{b}} ^{\mathrm{2}} −{c}_{{c}} ^{\mathrm{2}} +\mathrm{2}{c}_{{a}} {c}_{{b}} {c}_{{c}} \\ $$
Answered by math1967 last updated on 21/Jan/19
![[cosA−cos(B+C)][cos(B−C)−cos A] cos A{cos (B−C)+cos (B+C)}−cos^2 A−cos^2 B−cos^2 C+1★ 1−cos^2 A−cos^2 B−cos^2 C+2cos Acos Bcos C [cos (B−C)cos (B+C)=cos^2 B+cos^2 C−1]★](https://www.tinkutara.com/question/Q53399.png)
$$\left[{cosA}−{cos}\left({B}+{C}\right)\right]\left[{cos}\left({B}−{C}\right)−\mathrm{cos}\:{A}\right] \\ $$$$\mathrm{cos}\:{A}\left\{\mathrm{cos}\:\left({B}−{C}\right)+\mathrm{cos}\:\left({B}+{C}\right)\right\}−\mathrm{cos}\:^{\mathrm{2}} {A}−\mathrm{cos}\:^{\mathrm{2}} {B}−\mathrm{cos}\:^{\mathrm{2}} {C}+\mathrm{1}\bigstar \\ $$$$\mathrm{1}−\mathrm{cos}\:^{\mathrm{2}} {A}−\mathrm{cos}\:^{\mathrm{2}} {B}−\mathrm{cos}\:^{\mathrm{2}} {C}+\mathrm{2cos}\:{A}\mathrm{cos}\:{B}\mathrm{cos}\:{C} \\ $$$$\left[\mathrm{cos}\:\left({B}−{C}\right)\mathrm{cos}\:\left({B}+{C}\right)=\mathrm{cos}\:^{\mathrm{2}} {B}+\mathrm{cos}\:^{\mathrm{2}} {C}−\mathrm{1}\right]\bigstar \\ $$
Commented by math1967 last updated on 21/Jan/19

$${welcome} \\ $$
Commented by Kunal12588 last updated on 21/Jan/19
$${thanks}\:{a}\:{lot}\:{sir}\:{i}\:{got}\:{my}\:{mistake} \\ $$
