Question Number 150880 by mathdanisur last updated on 16/Aug/21
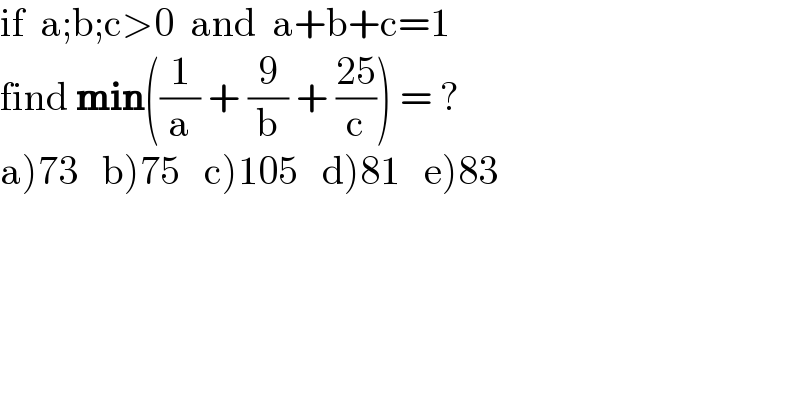
$$\mathrm{if}\:\:\mathrm{a};\mathrm{b};\mathrm{c}>\mathrm{0}\:\:\mathrm{and}\:\:\mathrm{a}+\mathrm{b}+\mathrm{c}=\mathrm{1} \\ $$$$\mathrm{find}\:\boldsymbol{\mathrm{min}}\left(\frac{\mathrm{1}}{\mathrm{a}}\:+\:\frac{\mathrm{9}}{\mathrm{b}}\:+\:\frac{\mathrm{25}}{\mathrm{c}}\right)\:=\:? \\ $$$$\left.\mathrm{a}\left.\right)\left.\mathrm{7}\left.\mathrm{3}\left.\:\:\:\mathrm{b}\right)\mathrm{75}\:\:\:\mathrm{c}\right)\mathrm{105}\:\:\:\mathrm{d}\right)\mathrm{81}\:\:\:\mathrm{e}\right)\mathrm{83} \\ $$
Answered by mr W last updated on 16/Aug/21
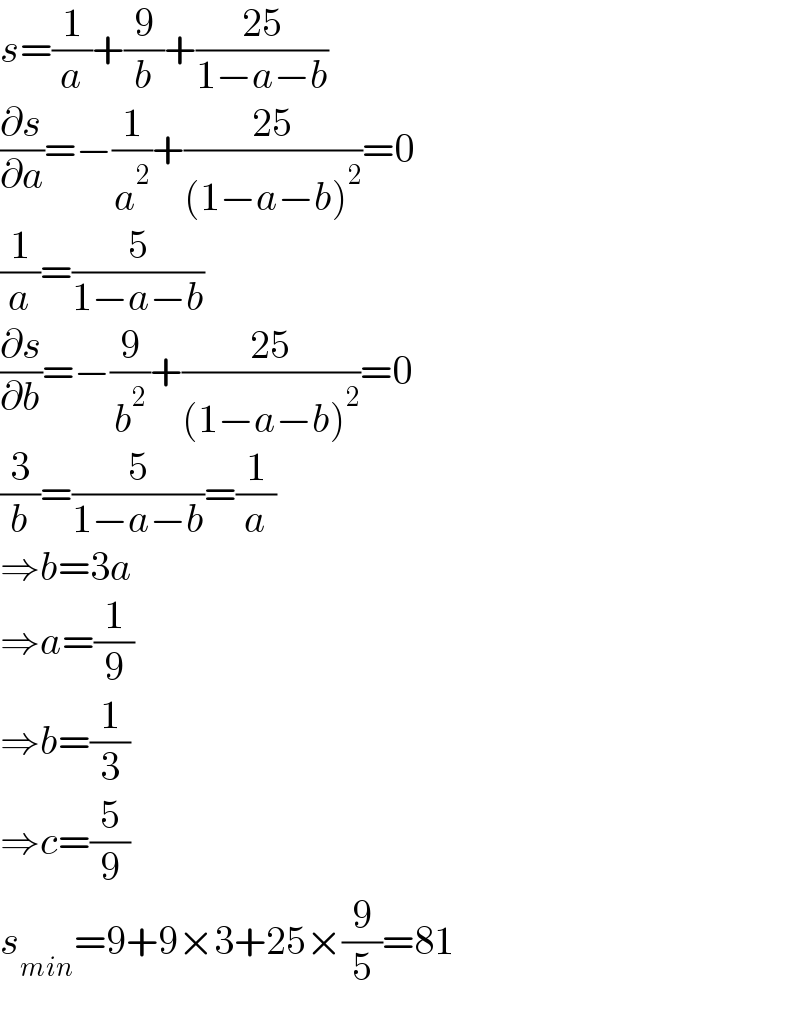
$${s}=\frac{\mathrm{1}}{{a}}+\frac{\mathrm{9}}{{b}}+\frac{\mathrm{25}}{\mathrm{1}−{a}−{b}} \\ $$$$\frac{\partial{s}}{\partial{a}}=−\frac{\mathrm{1}}{{a}^{\mathrm{2}} }+\frac{\mathrm{25}}{\left(\mathrm{1}−{a}−{b}\right)^{\mathrm{2}} }=\mathrm{0} \\ $$$$\frac{\mathrm{1}}{{a}}=\frac{\mathrm{5}}{\mathrm{1}−{a}−{b}} \\ $$$$\frac{\partial{s}}{\partial{b}}=−\frac{\mathrm{9}}{{b}^{\mathrm{2}} }+\frac{\mathrm{25}}{\left(\mathrm{1}−{a}−{b}\right)^{\mathrm{2}} }=\mathrm{0} \\ $$$$\frac{\mathrm{3}}{{b}}=\frac{\mathrm{5}}{\mathrm{1}−{a}−{b}}=\frac{\mathrm{1}}{{a}} \\ $$$$\Rightarrow{b}=\mathrm{3}{a} \\ $$$$\Rightarrow{a}=\frac{\mathrm{1}}{\mathrm{9}} \\ $$$$\Rightarrow{b}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\Rightarrow{c}=\frac{\mathrm{5}}{\mathrm{9}} \\ $$$${s}_{{min}} =\mathrm{9}+\mathrm{9}×\mathrm{3}+\mathrm{25}×\frac{\mathrm{9}}{\mathrm{5}}=\mathrm{81} \\ $$
Commented by mathdanisur last updated on 16/Aug/21

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{Ser} \\ $$
Answered by qaz last updated on 16/Aug/21
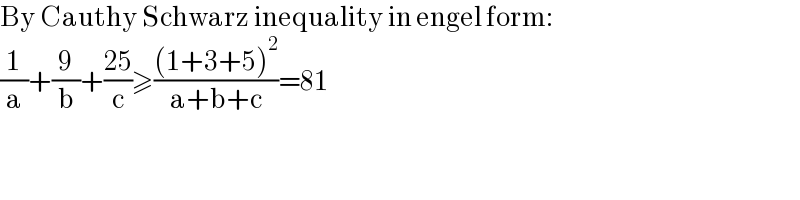
$$\mathrm{By}\:\mathrm{Cauthy}\:\mathrm{Schwarz}\:\mathrm{inequality}\:\mathrm{in}\:\mathrm{engel}\:\mathrm{form}: \\ $$$$\frac{\mathrm{1}}{\mathrm{a}}+\frac{\mathrm{9}}{\mathrm{b}}+\frac{\mathrm{25}}{\mathrm{c}}\geqslant\frac{\left(\mathrm{1}+\mathrm{3}+\mathrm{5}\right)^{\mathrm{2}} }{\mathrm{a}+\mathrm{b}+\mathrm{c}}=\mathrm{81} \\ $$
Commented by mathdanisur last updated on 16/Aug/21

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{Ser} \\ $$
