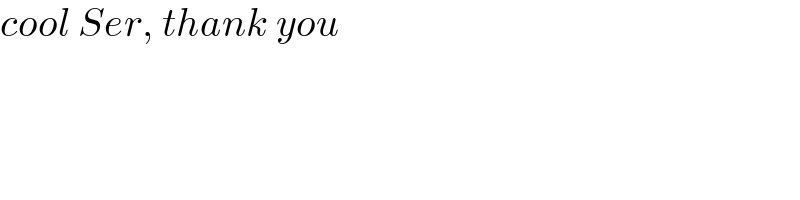if-a-b-c-R-find-abc-1-3-1-a-1-2b-1-4c-min-

Question Number 145383 by mathdanisur last updated on 04/Jul/21

i f a; b; c \in R^{+}

f i n d {(\sqrt[3]{a b c} + \frac{1}{a} + \frac{1}{2 b} + \frac{1}{4 c})}_{m i n} = ?

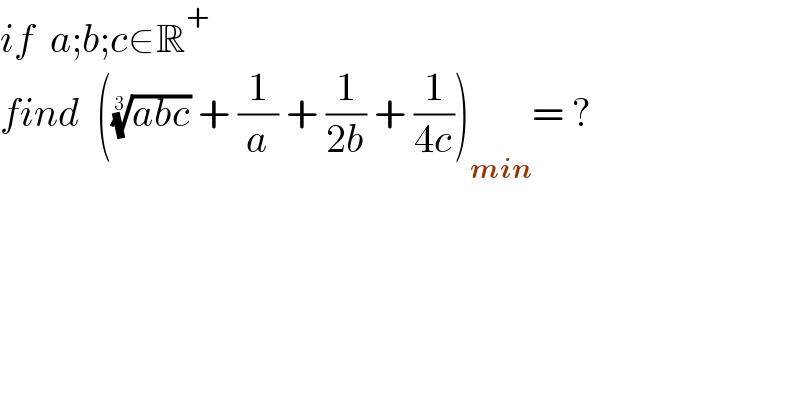
Answered by mnjuly1970 last updated on 04/Jul/21

A ⩾ \sqrt[3]{a b c} + 3 \sqrt[3]{\frac{1}{8 a b c}}

= \sqrt[3]{a b c} + \frac{3}{2} \sqrt[3]{\frac{1}{a b c}} \overset{a m - g m}{⩾} 2 \sqrt{\frac{3}{2}}

A_{m i n} = 2 \sqrt{\frac{3}{2}} = \sqrt{6}

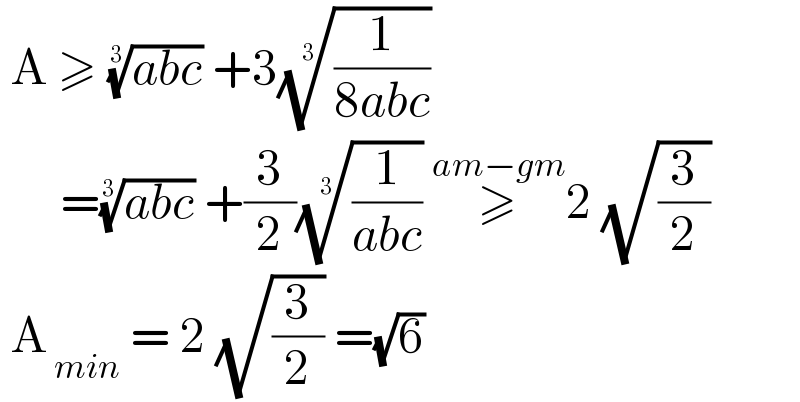
Commented by mathdanisur last updated on 04/Jul/21

T h a n k s S i r, a n s w e r \sqrt{6}

Commented by mnjuly1970 last updated on 04/Jul/21

t h a n k y o u s o m u c h a n d

y o u r m e n t i o n \dots

Commented by mathdanisur last updated on 04/Jul/21

c o o l S e r, t h a n k y o u

Answered by ajfour last updated on 04/Jul/21

l e t \frac{1}{a} = x, \frac{1}{2 b} = y, \frac{1}{4 c} = z

\Rightarrow f (x, y, z) = \frac{1 / 2}{{(x y z)}^{1 / 3}} + x + y + z

m i n i m u m s h o u l d o f c o u r s e

b e w h e n x = y = z (s y m m e t r y)

\Rightarrow f_{m i n} = \frac{1}{2 x} + 3 x

w h e r e \frac{1}{2 x} = 3 x \Rightarrow x^{2} = \frac{1}{6}

f_{m i n} = 6 x = \frac{6}{\sqrt{6}} = \sqrt{6} .

Commented by mathdanisur last updated on 04/Jul/21

c o o l S e r, t h a n k y o u