Question Number 103654 by Study last updated on 16/Jul/20
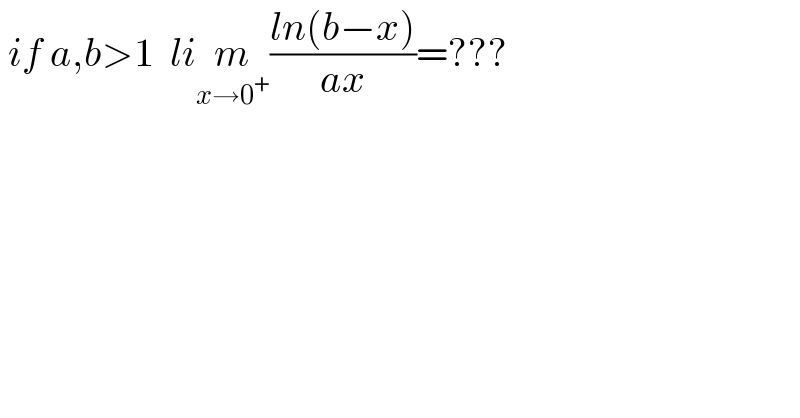
$$\:{if}\:{a},{b}>\mathrm{1}\:\:{li}\underset{{x}\rightarrow\mathrm{0}^{+} } {{m}}\frac{{ln}\left({b}−{x}\right)}{{ax}}=??? \\ $$
Answered by Worm_Tail last updated on 16/Jul/20
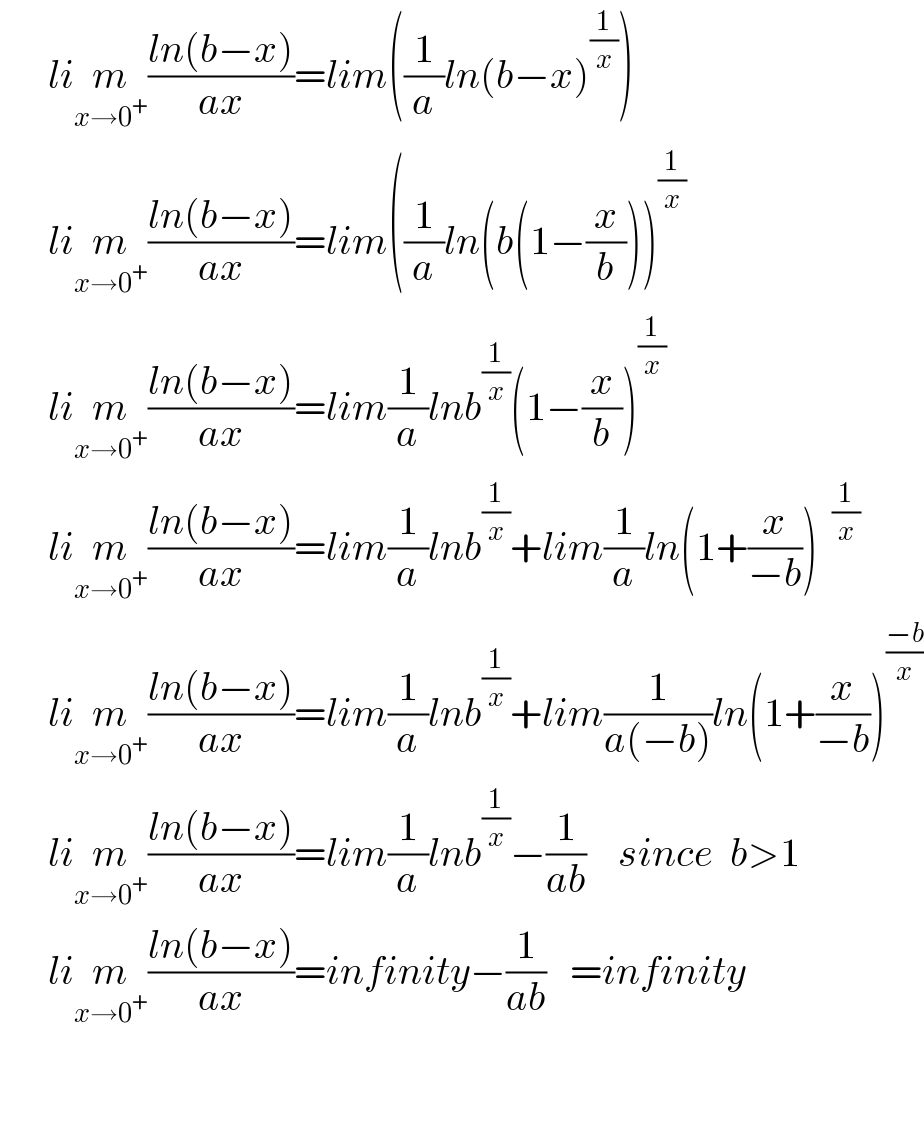
$$\:\:\:\:\:\:{li}\underset{{x}\rightarrow\mathrm{0}^{+} } {{m}}\frac{{ln}\left({b}−{x}\right)}{{ax}}={lim}\left(\frac{\mathrm{1}}{{a}}{ln}\left({b}−{x}\right)^{\frac{\mathrm{1}}{{x}}} \right) \\ $$$$\:\:\:\:\:\:{li}\underset{{x}\rightarrow\mathrm{0}^{+} } {{m}}\frac{{ln}\left({b}−{x}\right)}{{ax}}={lim}\left(\frac{\mathrm{1}}{{a}}{ln}\left({b}\left(\mathrm{1}−\frac{{x}}{{b}}\right)\right)^{\frac{\mathrm{1}}{{x}}} \right. \\ $$$$\:\:\:\:\:\:{li}\underset{{x}\rightarrow\mathrm{0}^{+} } {{m}}\frac{{ln}\left({b}−{x}\right)}{{ax}}={lim}\frac{\mathrm{1}}{{a}}{lnb}^{\frac{\mathrm{1}}{{x}}} \left(\mathrm{1}−\frac{{x}}{{b}}\right)^{\frac{\mathrm{1}}{{x}}} \\ $$$$\:\:\:\:\:\:{li}\underset{{x}\rightarrow\mathrm{0}^{+} } {{m}}\frac{{ln}\left({b}−{x}\right)}{{ax}}={lim}\frac{\mathrm{1}}{{a}}{lnb}^{\frac{\mathrm{1}}{{x}}} +{lim}\frac{\mathrm{1}}{{a}}{ln}\left(\mathrm{1}+\frac{{x}}{−{b}}\right) \\ $$$$\:\:\:\:\:\:{li}\underset{{x}\rightarrow\mathrm{0}^{+} } {{m}}\frac{{ln}\left({b}−{x}\right)}{{ax}}={lim}\frac{\mathrm{1}}{{a}}{lnb}^{\frac{\mathrm{1}}{{x}}} +{lim}\frac{\mathrm{1}}{{a}\left(−{b}\right)}{ln}\left(\mathrm{1}+\frac{{x}}{−{b}}\right)^{\frac{−{b}}{{x}}} \\ $$$$\:\:\:\:\:\:{li}\underset{{x}\rightarrow\mathrm{0}^{+} } {{m}}\frac{{ln}\left({b}−{x}\right)}{{ax}}={lim}\frac{\mathrm{1}}{{a}}{lnb}^{\frac{\mathrm{1}}{{x}}} −\frac{\mathrm{1}}{{ab}}\:\:\:\:{since}\:\:{b}>\mathrm{1} \\ $$$$\:\:\:\:\:\:{li}\underset{{x}\rightarrow\mathrm{0}^{+} } {{m}}\frac{{ln}\left({b}−{x}\right)}{{ax}}={infinity}−\frac{\mathrm{1}}{{ab}}\:\:\:={infinity} \\ $$$$\:\:\:\: \\ $$$$\:\:\:\: \\ $$
