Menu Close

If-a-b-R-satisfy-a-4-b-4-6a-2-b-2-9-and-ab-a-b-a-b-11-then-a-2-b-2-

Tinku Tara 0 Comments
Pin




Question Number 151198 by liberty last updated on 19/Aug/21
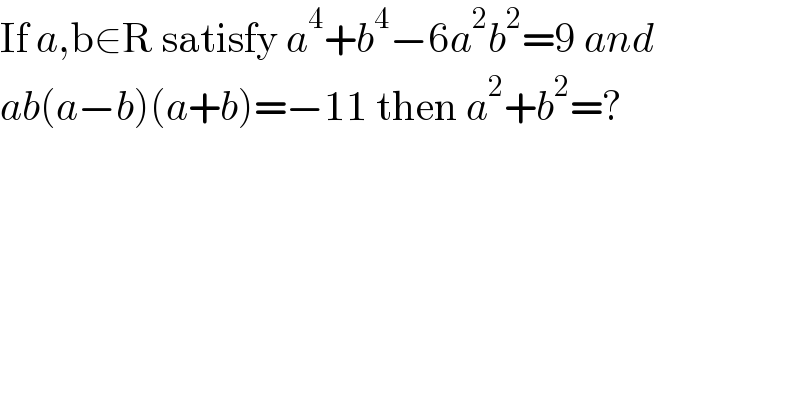
If a,b∈R satisfy a^4 +b^4 −6a^2 b^2 =9 and ab(a−b)(a+b)=−11 then a^2 +b^2 =?
$$\mathrm{If}\:{a},\mathrm{b}\in\mathrm{R}\:\mathrm{satisfy}\:{a}^{\mathrm{4}} +{b}^{\mathrm{4}} −\mathrm{6}{a}^{\mathrm{2}} {b}^{\mathrm{2}} =\mathrm{9}\:{and} \\ $$$${ab}\left({a}−{b}\right)\left({a}+{b}\right)=−\mathrm{11}\:\mathrm{then}\:{a}^{\mathrm{2}} +{b}^{\mathrm{2}} =? \\ $$
Answered by EDWIN88 last updated on 19/Aug/21
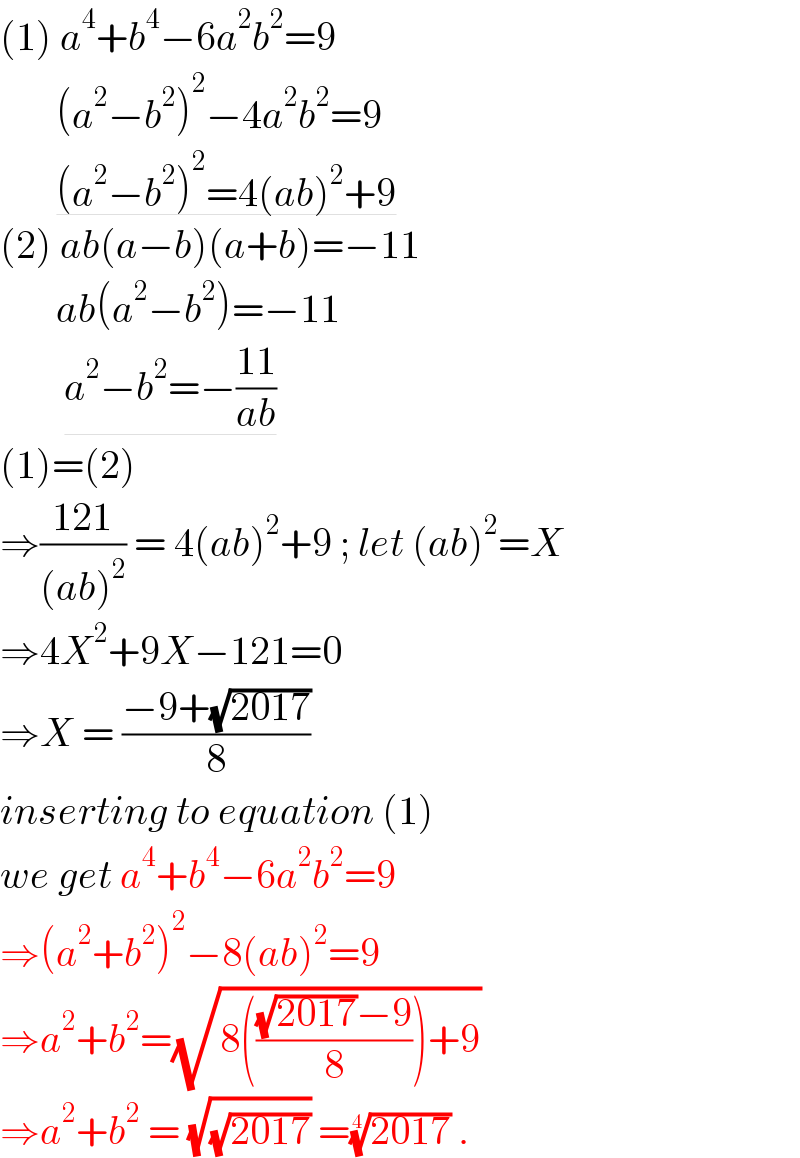
(1) a^4 +b^4 −6a^2 b^2 =9 (a^2 −b^2 )^2 −4a^2 b^2 =9 (a^2 −b^2 )^2 =4(ab)^2 +9 (2) ab(a−b)(a+b)=−11 ab(a^2 −b^2 )=−11 a^2 −b^2 =−((11)/(ab)) (1)=(2) ⇒((121)/((ab)^2 )) = 4(ab)^2 +9 ; let (ab)^2 =X ⇒4X^2 +9X−121=0 ⇒X = ((−9+(√(2017)))/8) inserting to equation (1) we get a^4 +b^4 −6a^2 b^2 =9 ⇒(a^2 +b^2 )^2 −8(ab)^2 =9 ⇒a^2 +b^2 =(√(8((((√(2017))−9)/8))+9)) ⇒a^2 +b^2 = (√(√(2017))) =((2017))^(1/4) .
$$\left(\mathrm{1}\right)\:{a}^{\mathrm{4}} +{b}^{\mathrm{4}} −\mathrm{6}{a}^{\mathrm{2}} {b}^{\mathrm{2}} =\mathrm{9} \\ $$$$\:\:\:\:\:\:\:\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)^{\mathrm{2}} −\mathrm{4}{a}^{\mathrm{2}} {b}^{\mathrm{2}} =\mathrm{9} \\ $$$$\:\:\:\:\:\:\:\underline{\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)^{\mathrm{2}} =\mathrm{4}\left({ab}\right)^{\mathrm{2}} +\mathrm{9}}\: \\ $$$$\left(\mathrm{2}\right)\:{ab}\left({a}−{b}\right)\left({a}+{b}\right)=−\mathrm{11} \\ $$$$\:\:\:\:\:\:\:{ab}\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)=−\mathrm{11}\: \\ $$$$\:\:\:\:\:\:\:\:\underline{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} =−\frac{\mathrm{11}}{{ab}}} \\ $$$$\left(\mathrm{1}\right)=\left(\mathrm{2}\right) \\ $$$$\Rightarrow\frac{\mathrm{121}}{\left({ab}\right)^{\mathrm{2}} }\:=\:\mathrm{4}\left({ab}\right)^{\mathrm{2}} +\mathrm{9}\:;\:{let}\:\left({ab}\right)^{\mathrm{2}} ={X} \\ $$$$\Rightarrow\mathrm{4}{X}^{\mathrm{2}} +\mathrm{9}{X}−\mathrm{121}=\mathrm{0} \\ $$$$\Rightarrow{X}\:=\:\frac{−\mathrm{9}+\sqrt{\mathrm{2017}}}{\mathrm{8}}\: \\ $$$${inserting}\:{to}\:{equation}\:\left(\mathrm{1}\right) \\ $$$${we}\:{get}\:{a}^{\mathrm{4}} +{b}^{\mathrm{4}} −\mathrm{6}{a}^{\mathrm{2}} {b}^{\mathrm{2}} =\mathrm{9} \\ $$$$\Rightarrow\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)^{\mathrm{2}} −\mathrm{8}\left({ab}\right)^{\mathrm{2}} =\mathrm{9} \\ $$$$\Rightarrow{a}^{\mathrm{2}} +{b}^{\mathrm{2}} =\sqrt{\mathrm{8}\left(\frac{\sqrt{\mathrm{2017}}−\mathrm{9}}{\mathrm{8}}\right)+\mathrm{9}} \\ $$$$\Rightarrow{a}^{\mathrm{2}} +{b}^{\mathrm{2}} \:=\:\sqrt{\sqrt{\mathrm{2017}}}\:=\sqrt[{\mathrm{4}}]{\mathrm{2017}}\:. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *