Menu Close

If-a-Cos-iSin-and-b-Cos-iSin-Prove-that-a-b-1-ab-a-b-1-ab-Sin-Sin-Sin-Sin-

Tinku Tara 0 Comments
Pin




Question Number 61799 by alphaprime last updated on 08/Jun/19
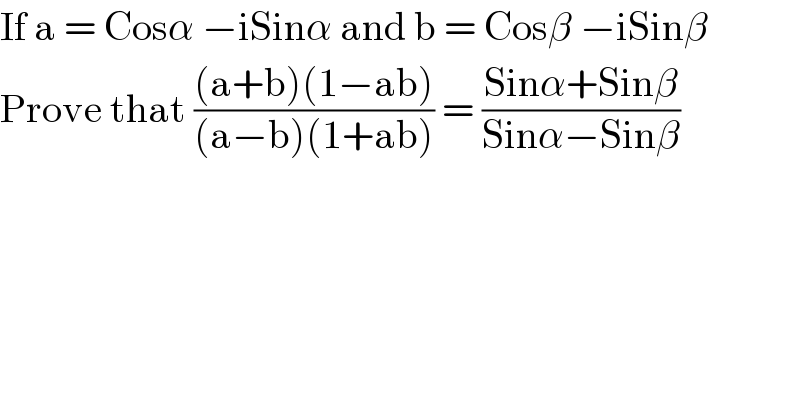
If a = Cosα −iSinα and b = Cosβ −iSinβ Prove that (((a+b)(1−ab))/((a−b)(1+ab))) = ((Sinα+Sinβ)/(Sinα−Sinβ))
$$\mathrm{If}\:\mathrm{a}\:=\:\mathrm{Cos}\alpha\:−\mathrm{iSin}\alpha\:\mathrm{and}\:\mathrm{b}\:=\:\mathrm{Cos}\beta\:−\mathrm{iSin}\beta \\ $$$$\mathrm{Prove}\:\mathrm{that}\:\frac{\left(\mathrm{a}+\mathrm{b}\right)\left(\mathrm{1}−\mathrm{ab}\right)}{\left(\mathrm{a}−\mathrm{b}\right)\left(\mathrm{1}+\mathrm{ab}\right)}\:=\:\frac{\mathrm{Sin}\alpha+\mathrm{Sin}\beta}{\mathrm{Sin}\alpha−\mathrm{Sin}\beta} \\ $$
Answered by tanmay last updated on 09/Jun/19
a=e^(−iα) b=e^(−iβ) (a/b)=e^(−i(∝−β)) ab=e^(−i(α+β)) (a/b)=(e^(−i(α−β)) /1) ((a+b)/(a−b))=((e^(−i(α−β)) +1)/(e^(−i(α−β)) −1)) (1/(ab))=(1/e^(−i(α+β)) )=(e^(i(α+β)) /1) ((1−ab)/(1+ab))=((e^(i(α+β)) −1)/(1+e^(i(α+β)) )) now ((a+b)/(a−b))×((1−ab)/(1+ab)) =((e^(−i(α−β)) +1)/(e^(−i(α−β)) −1))×((e^(i(α+β) )−1)/(e^(i(α+β)) +1)) =((e^(i(α+β−α+β)) +e^(i(α+β)) −e^(−i(α−β)) −1)/(e^(i(α+β−α+β)) −e^(i(α+β)) +e^(−i(α−β)) −1)) =((cos2β+isin2β+cos(α+β)+isin(α+β)−cos(α−β)+isin(α−β)−1)/(cos2β+isi2β−cos(α+β)−isin(α+β)+cos(α−β)−isin(α−β)−1)) =((cos2β−1−2sinαsinβ+i(sin2β+sin(α+β)+sin(α−β)))/(cos2β−1+2siαsinβ+i(sin2β−sin(α+β)−sin(α−β)))) =((−2sin^2 β−2sinαsinβ+i(sin2β+2sinαcosβ))/(−2sin^2 β+2sinαsinβ+i(sin2β−2sinαcosβ))) =((−2sin^2 β−2sinαsinβ+i(2sinβcosβ+2sinαcosβ))/(−2sin^2 β+2sinαsinβ+i(2sinβcosβ−2sinαcosβ))) =((−2sinβ(sinβ+sinα)+i2cosβ(sinα+sinβ))/(−2sinβ(sinβ−sinα)+i2cosβ(sinβ−sinα))) =(((sinα+sinβ)(−2sinβ+i2cosβ))/((sinβ−sinα)(−2sinβ+i2cosβ))) =((sinα+sinβ)/(sinβ−sinα)) pls check mistake if any
$${a}={e}^{−{i}\alpha} \:\:\:{b}={e}^{−{i}\beta} \\ $$$$\frac{{a}}{{b}}={e}^{−{i}\left(\propto−\beta\right)} \:\:\:\:\:\:{ab}={e}^{−{i}\left(\alpha+\beta\right)} \\ $$$$\frac{{a}}{{b}}=\frac{{e}^{−{i}\left(\alpha−\beta\right)} }{\mathrm{1}} \\ $$$$\frac{{a}+{b}}{{a}−{b}}=\frac{{e}^{−{i}\left(\alpha−\beta\right)} +\mathrm{1}}{{e}^{−{i}\left(\alpha−\beta\right)} −\mathrm{1}} \\ $$$$\frac{\mathrm{1}}{{ab}}=\frac{\mathrm{1}}{{e}^{−{i}\left(\alpha+\beta\right)} }=\frac{{e}^{{i}\left(\alpha+\beta\right)} }{\mathrm{1}} \\ $$$$\frac{\mathrm{1}−{ab}}{\mathrm{1}+{ab}}=\frac{{e}^{{i}\left(\alpha+\beta\right)} −\mathrm{1}}{\mathrm{1}+{e}^{{i}\left(\alpha+\beta\right)} } \\ $$$${now}\:\frac{{a}+{b}}{{a}−{b}}×\frac{\mathrm{1}−{ab}}{\mathrm{1}+{ab}} \\ $$$$=\frac{{e}^{−{i}\left(\alpha−\beta\right)} +\mathrm{1}}{{e}^{−{i}\left(\alpha−\beta\right)} −\mathrm{1}}×\frac{\left.{e}^{{i}\left(\alpha+\beta\right.} \right)−\mathrm{1}}{{e}^{{i}\left(\alpha+\beta\right)} +\mathrm{1}} \\ $$$$=\frac{{e}^{{i}\left(\alpha+\beta−\alpha+\beta\right)} +{e}^{{i}\left(\alpha+\beta\right)} −{e}^{−{i}\left(\alpha−\beta\right)} −\mathrm{1}}{{e}^{{i}\left(\alpha+\beta−\alpha+\beta\right)} −{e}^{{i}\left(\alpha+\beta\right)} +{e}^{−{i}\left(\alpha−\beta\right)} −\mathrm{1}} \\ $$$$=\frac{{cos}\mathrm{2}\beta+{isin}\mathrm{2}\beta+{cos}\left(\alpha+\beta\right)+{isin}\left(\alpha+\beta\right)−{cos}\left(\alpha−\beta\right)+{isin}\left(\alpha−\beta\right)−\mathrm{1}}{{cos}\mathrm{2}\beta+{isi}\mathrm{2}\beta−{cos}\left(\alpha+\beta\right)−{isin}\left(\alpha+\beta\right)+{cos}\left(\alpha−\beta\right)−{isin}\left(\alpha−\beta\right)−\mathrm{1}} \\ $$$$=\frac{{cos}\mathrm{2}\beta−\mathrm{1}−\mathrm{2}{sin}\alpha{sin}\beta+{i}\left({sin}\mathrm{2}\beta+{sin}\left(\alpha+\beta\right)+{sin}\left(\alpha−\beta\right)\right)}{{cos}\mathrm{2}\beta−\mathrm{1}+\mathrm{2}{si}\alpha{sin}\beta+{i}\left({sin}\mathrm{2}\beta−{sin}\left(\alpha+\beta\right)−{sin}\left(\alpha−\beta\right)\right)} \\ $$$$=\frac{−\mathrm{2}{sin}^{\mathrm{2}} \beta−\mathrm{2}{sin}\alpha{sin}\beta+{i}\left({sin}\mathrm{2}\beta+\mathrm{2}{sin}\alpha{cos}\beta\right)}{−\mathrm{2}{sin}^{\mathrm{2}} \beta+\mathrm{2}{sin}\alpha{sin}\beta+{i}\left({sin}\mathrm{2}\beta−\mathrm{2}{sin}\alpha{cos}\beta\right)} \\ $$$$=\frac{−\mathrm{2}{sin}^{\mathrm{2}} \beta−\mathrm{2}{sin}\alpha{sin}\beta+{i}\left(\mathrm{2}{sin}\beta{cos}\beta+\mathrm{2}{sin}\alpha{cos}\beta\right)}{−\mathrm{2}{sin}^{\mathrm{2}} \beta+\mathrm{2}{sin}\alpha{sin}\beta+{i}\left(\mathrm{2}{sin}\beta{cos}\beta−\mathrm{2}{sin}\alpha{cos}\beta\right)} \\ $$$$=\frac{−\mathrm{2}{sin}\beta\left({sin}\beta+{sin}\alpha\right)+{i}\mathrm{2}{cos}\beta\left({sin}\alpha+{sin}\beta\right)}{−\mathrm{2}{sin}\beta\left({sin}\beta−{sin}\alpha\right)+{i}\mathrm{2}{cos}\beta\left({sin}\beta−{sin}\alpha\right)} \\ $$$$=\frac{\left({sin}\alpha+{sin}\beta\right)\left(−\mathrm{2}{sin}\beta+{i}\mathrm{2}{cos}\beta\right)}{\left({sin}\beta−{sin}\alpha\right)\left(−\mathrm{2}{sin}\beta+{i}\mathrm{2}{cos}\beta\right)} \\ $$$$=\frac{{sin}\alpha+{sin}\beta}{{sin}\beta−{sin}\alpha} \\ $$$${pls}\:{check}\:{mistake}\:{if}\:{any} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *