Menu Close

If-a-fraction-is-added-to-its-denominator-it-reduces-to-1-2-and-when-the-same-fraction-added-to-numerator-it-also-reduces-to-2-3-a-what-is-the-fraction-b-find-the-square-root-such-that-th

Tinku Tara 0 Comments
Pin




Question Number 41879 by Tawa1 last updated on 14/Aug/18
If a fraction is added to its denominator , it reduces to (1/2) and when the same fraction added to numerator, it also reduces to (2/3) (a) what is the fraction (b) find the square root such that the result of the fraction is less than 1
$$\mathrm{If}\:\mathrm{a}\:\mathrm{fraction}\:\mathrm{is}\:\mathrm{added}\:\mathrm{to}\:\mathrm{its}\:\mathrm{denominator}\:,\:\:\mathrm{it}\:\mathrm{reduces}\:\mathrm{to}\:\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{and}\: \\ $$$$\mathrm{when}\:\mathrm{the}\:\mathrm{same}\:\mathrm{fraction}\:\mathrm{added}\:\mathrm{to}\:\mathrm{numerator},\:\mathrm{it}\:\mathrm{also}\:\mathrm{reduces}\:\mathrm{to}\:\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\left(\mathrm{a}\right)\:\mathrm{what}\:\mathrm{is}\:\mathrm{the}\:\mathrm{fraction} \\ $$$$\left(\mathrm{b}\right)\:\mathrm{find}\:\mathrm{the}\:\mathrm{square}\:\mathrm{root}\:\mathrm{such}\:\mathrm{that}\:\mathrm{the}\:\mathrm{result}\:\mathrm{of}\:\mathrm{the}\:\mathrm{fraction}\:\mathrm{is}\:\mathrm{less} \\ $$$$\mathrm{than}\:\mathrm{1} \\ $$$$ \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 14/Aug/18
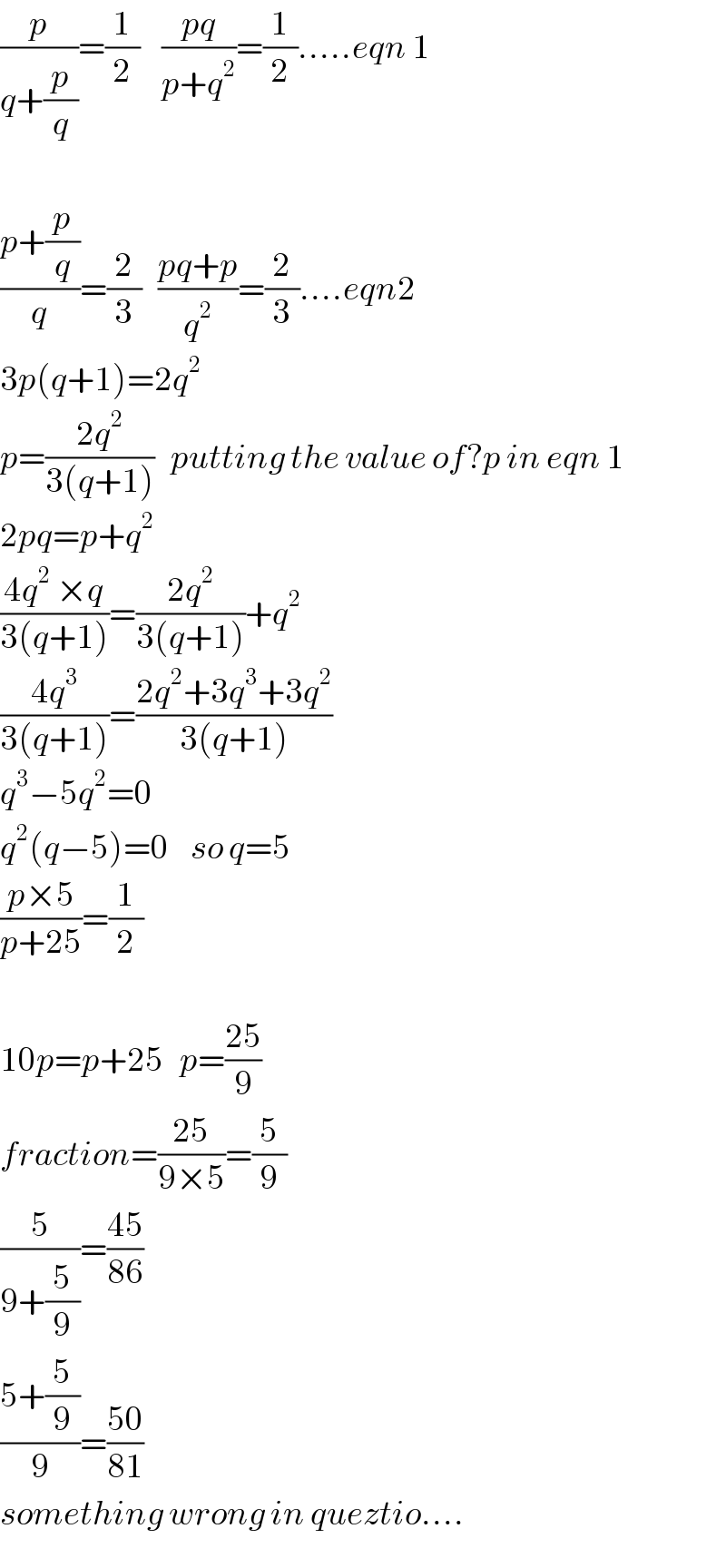
(p/(q+(p/q)))=(1/2) ((pq)/(p+q^2 ))=(1/2).....eqn 1 ((p+(p/q))/q)=(2/3) ((pq+p)/q^2 )=(2/3)....eqn2 3p(q+1)=2q^2 p=((2q^2 )/(3(q+1))) putting the value of?p in eqn 1 2pq=p+q^2 ((4q^2 ×q)/(3(q+1)))=((2q^2 )/(3(q+1)))+q^2 ((4q^3 )/(3(q+1)))=((2q^2 +3q^3 +3q^2 )/(3(q+1))) q^3 −5q^2 =0 q^2 (q−5)=0 so q=5 ((p×5)/(p+25))=(1/2) 10p=p+25 p=((25)/9) fraction=((25)/(9×5))=(5/9) (5/(9+(5/9)))=((45)/(86)) ((5+(5/9))/9)=((50)/(81)) something wrong in queztio....
$$\frac{{p}}{{q}+\frac{{p}}{{q}}}=\frac{\mathrm{1}}{\mathrm{2}}\:\:\:\:\frac{{pq}}{{p}+{q}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{2}}…..{eqn}\:\mathrm{1} \\ $$$$ \\ $$$$\frac{{p}+\frac{{p}}{{q}}}{{q}}=\frac{\mathrm{2}}{\mathrm{3}}\:\:\:\frac{{pq}+{p}}{{q}^{\mathrm{2}} }=\frac{\mathrm{2}}{\mathrm{3}}….{eqn}\mathrm{2} \\ $$$$\mathrm{3}{p}\left({q}+\mathrm{1}\right)=\mathrm{2}{q}^{\mathrm{2}} \\ $$$${p}=\frac{\mathrm{2}{q}^{\mathrm{2}} }{\mathrm{3}\left({q}+\mathrm{1}\right)}\:\:\:{putting}\:{the}\:{value}\:{of}?{p}\:{in}\:{eqn}\:\mathrm{1} \\ $$$$\mathrm{2}{pq}={p}+{q}^{\mathrm{2}} \\ $$$$\frac{\mathrm{4}{q}^{\mathrm{2}} \:×{q}}{\mathrm{3}\left({q}+\mathrm{1}\right)}=\frac{\mathrm{2}{q}^{\mathrm{2}} }{\mathrm{3}\left({q}+\mathrm{1}\right)}+{q}^{\mathrm{2}} \\ $$$$\frac{\mathrm{4}{q}^{\mathrm{3}} }{\mathrm{3}\left({q}+\mathrm{1}\right)}=\frac{\mathrm{2}{q}^{\mathrm{2}} +\mathrm{3}{q}^{\mathrm{3}} +\mathrm{3}{q}^{\mathrm{2}} }{\mathrm{3}\left({q}+\mathrm{1}\right)} \\ $$$${q}^{\mathrm{3}} −\mathrm{5}{q}^{\mathrm{2}} =\mathrm{0} \\ $$$${q}^{\mathrm{2}} \left({q}−\mathrm{5}\right)=\mathrm{0}\:\:\:\:{so}\:{q}=\mathrm{5} \\ $$$$\frac{{p}×\mathrm{5}}{{p}+\mathrm{25}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$ \\ $$$$\mathrm{10}{p}={p}+\mathrm{25}\:\:\:{p}=\frac{\mathrm{25}}{\mathrm{9}} \\ $$$${fraction}=\frac{\mathrm{25}}{\mathrm{9}×\mathrm{5}}=\frac{\mathrm{5}}{\mathrm{9}} \\ $$$$\frac{\mathrm{5}}{\mathrm{9}+\frac{\mathrm{5}}{\mathrm{9}}}=\frac{\mathrm{45}}{\mathrm{86}} \\ $$$$\frac{\mathrm{5}+\frac{\mathrm{5}}{\mathrm{9}}}{\mathrm{9}}=\frac{\mathrm{50}}{\mathrm{81}} \\ $$$${something}\:{wrong}\:{in}\:{queztio}…. \\ $$
Commented by Tawa1 last updated on 14/Aug/18
God bless you sir
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by MJS last updated on 15/Aug/18
the point is, the equations are solved for p=((25)/9) ∧ q=5 ⇒ you cannot set (p/q)=(5/9) and insert p=5 ∧ q=9 in the original equation we must first put p, q ∈Z or otherwise it′s no regular fraction. then at the point we get p=((25)/9) it′s not in our domain of definition ⇒ ⇒ the problem has no valid solution
$$\mathrm{the}\:\mathrm{point}\:\mathrm{is},\:\mathrm{the}\:\mathrm{equations}\:\mathrm{are}\:\mathrm{solved}\:\mathrm{for} \\ $$$${p}=\frac{\mathrm{25}}{\mathrm{9}}\:\wedge\:{q}=\mathrm{5}\:\Rightarrow\:\mathrm{you}\:\mathrm{cannot}\:\mathrm{set}\:\frac{{p}}{{q}}=\frac{\mathrm{5}}{\mathrm{9}}\:\mathrm{and}\:\mathrm{insert} \\ $$$${p}=\mathrm{5}\:\wedge\:{q}=\mathrm{9}\:\mathrm{in}\:\mathrm{the}\:\mathrm{original}\:\mathrm{equation} \\ $$$$ \\ $$$$\mathrm{we}\:\mathrm{must}\:\mathrm{first}\:\mathrm{put}\:{p},\:{q}\:\in\mathbb{Z}\:\mathrm{or}\:\mathrm{otherwise}\:\mathrm{it}'\mathrm{s}\:\mathrm{no} \\ $$$$\mathrm{regular}\:\mathrm{fraction}.\:\mathrm{then}\:\mathrm{at}\:\mathrm{the}\:\mathrm{point}\:\mathrm{we}\:\mathrm{get} \\ $$$${p}=\frac{\mathrm{25}}{\mathrm{9}}\:\mathrm{it}'\mathrm{s}\:\mathrm{not}\:\mathrm{in}\:\mathrm{our}\:\mathrm{domain}\:\mathrm{of}\:\mathrm{definition}\:\Rightarrow \\ $$$$\Rightarrow\:\mathrm{the}\:\mathrm{problem}\:\mathrm{has}\:\mathrm{no}\:\mathrm{valid}\:\mathrm{solution} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 15/Aug/18
thank you sir...
$${thank}\:{you}\:{sir}… \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *