If-a-log-24-12-b-log-36-24-and-c-log-48-36-then-1-abc-is-equal-to-A-2ab-B-2ac-C-2bc-D-0-

Question Number 113803 by Aina Samuel Temidayo last updated on 15/Sep/20

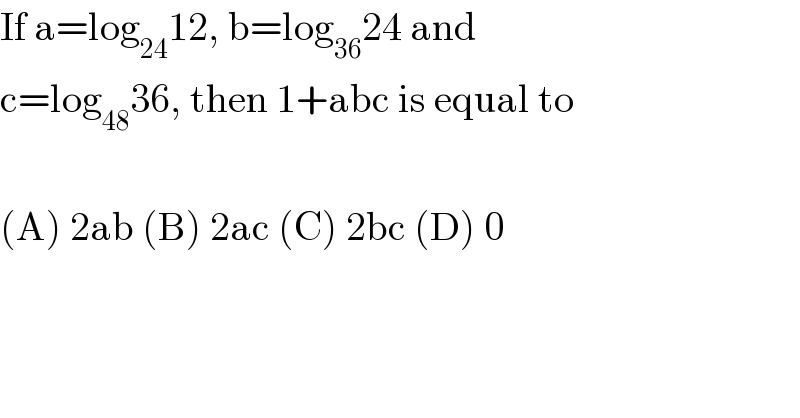
If a = \log_{24} 12, b = \log_{36} 24 and

c = \log_{48} 36, then 1 + abc is equal to

(A) 2 ab (B) 2 ac (C) 2 bc (D) 0

Answered by bemath last updated on 15/Sep/20

a = \frac{\ln 12}{\ln 24} = \frac{\ln 12}{\ln 2 + \ln 12}, b = \frac{\ln 24}{\ln 36} = \frac{\ln 2 + \ln 12}{\ln 3 + \ln 12}

c = \frac{\ln 3 + \ln 12}{\ln 4 + \ln 12}

a \times b \times c = \frac{\ln 12}{\ln 2 + \ln 12} \times \frac{\ln 2 + \ln 12}{\ln 3 + \ln 12} \times \frac{\ln 3 + \ln 12}{\ln 4 + \ln 12}

= \frac{\ln 12}{\ln 4 + \ln 12} = \log_{48} (12)

1 + a b c = 1 + \log_{48} (12)

= \log_{48} (12 \times 48)

= \frac{\ln 4 + 2 . \ln 12}{\ln 4 + \ln 12}

= \frac{2 \ln 2 + 2 \ln 12}{\ln 4 + \ln 12} = 2 (\frac{\ln 2 + \ln 12}{\ln 4 + \ln 12})

= 2 b c

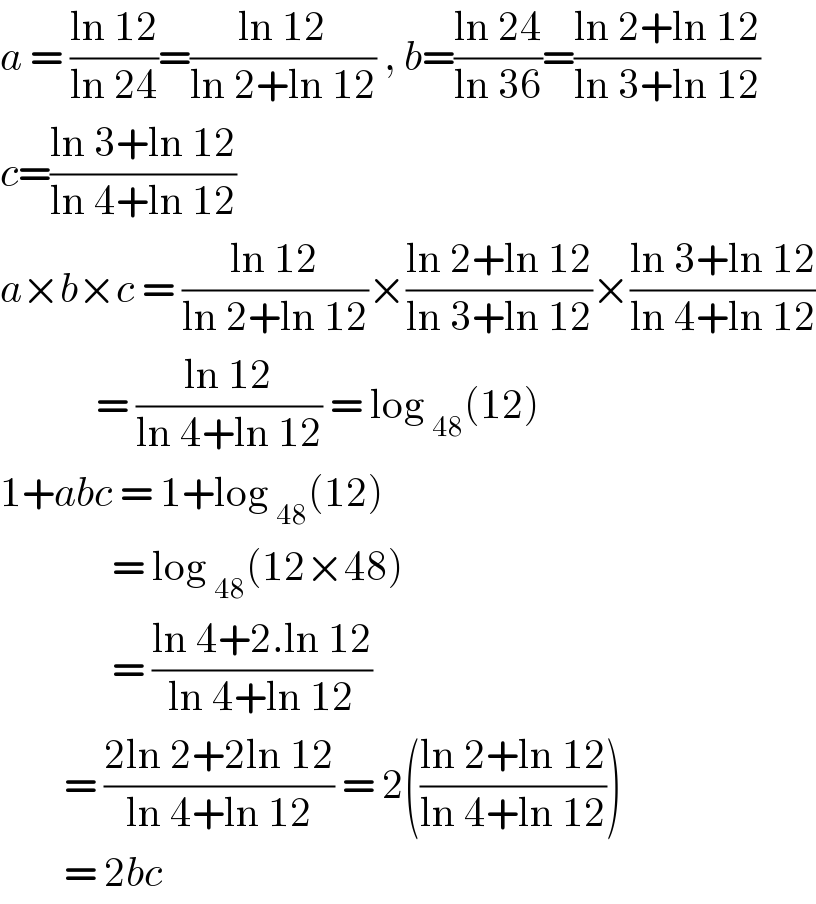
Commented by Aina Samuel Temidayo last updated on 15/Sep/20

Thanks .

Answered by som(math1967) last updated on 15/Sep/20

C) 2 bc

Answered by $@y@m last updated on 15/Sep/20

24^{a} = 12 \dots . . (A)

36^{b} = 24 \dots . . (B)

48^{c} = 36 \dots . . (C)

F r o m (C),

{(48^{c})}^{b} = 36^{b}

48^{b c} = 24 {u s i m g (B)

{(48^{b c})}^{a} = 24^{a}

48^{a b c} = 12 {u s i n g (A)

48^{a b c} \times 48 = 12 \times 48

48^{1 + a b c} = 24^{2}

48^{1 + a b c} = 36^{2 b}

48^{1 + a b c} = 48^{2 b c}

1 + a b c = 2 b c

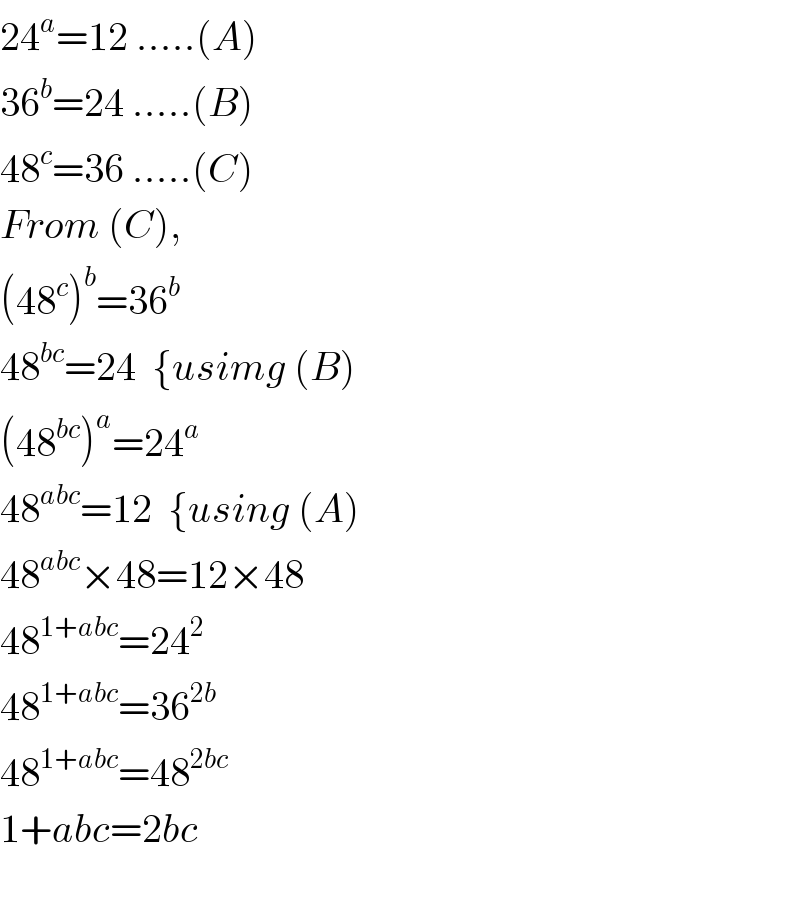
Commented by Aina Samuel Temidayo last updated on 15/Sep/20

Nice method . Thanks .