Question Number 147529 by mathdanisur last updated on 21/Jul/21
$${if}\:\:\:{a}_{\boldsymbol{{n}}+\mathrm{1}} \:=\:\sqrt{{a}_{\mathrm{1}} \:+\:{a}_{\boldsymbol{{n}}} } \\ $$$${find}\:\:\underset{\boldsymbol{{x}}\rightarrow\infty} {{lim}a}_{\boldsymbol{{n}}} \:=\:? \\ $$
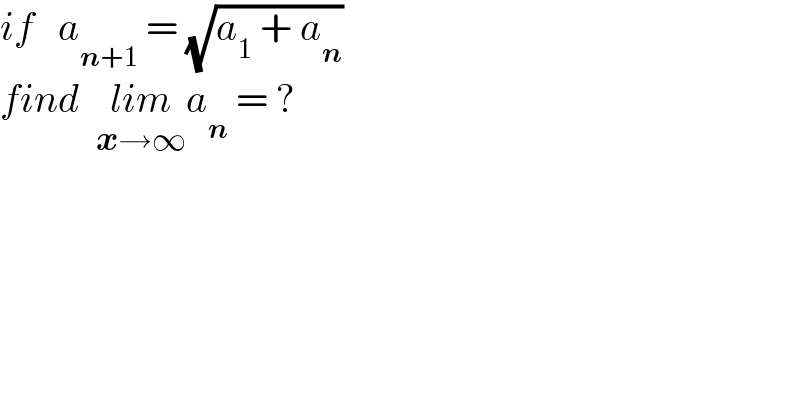
Commented by mathdanisur last updated on 21/Jul/21
$${Sorry}\:\:\boldsymbol{{a}}_{\mathrm{1}} \:=\:\mathrm{12} \\ $$
Answered by gsk2684 last updated on 21/Jul/21
$${L}=\underset{{n}\rightarrow\infty} {\mathrm{lim}}{a}_{{n}+\mathrm{1}} =\underset{{n}\rightarrow\infty} {\mathrm{lim}}\sqrt{{a}_{\mathrm{1}} +{a}_{{n}} }>\mathrm{0} \\ $$$${L}=\sqrt{{a}_{\mathrm{1}} +{L}} \\ $$$${L}^{\mathrm{2}} −{L}−{a}_{\mathrm{1}} =\mathrm{0} \\ $$$${L}=\frac{\mathrm{1}\pm\sqrt{\mathrm{1}+\mathrm{4}{a}_{\mathrm{1}} }}{\mathrm{2}}>\mathrm{0} \\ $$$${L}=\frac{\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{4}{a}_{\mathrm{1}} }}{\mathrm{2}}=\frac{\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{48}}}{\mathrm{2}}=\mathrm{4} \\ $$
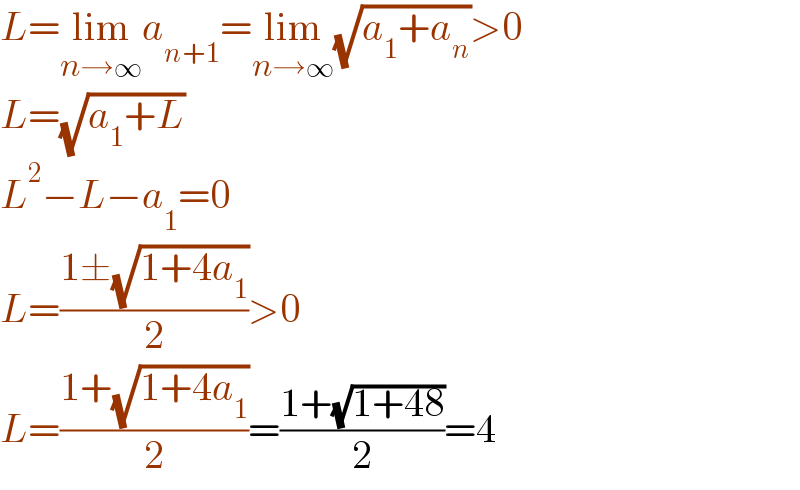
Commented by Snail last updated on 21/Jul/21
$${You}\:{are}\:{technically}\:{wrong}\:{in}\:{the}\:{second}\:{line} \\ $$$${while}\:{writing}\:{L}\:{u}\:{havd}\:{to}\:{show}\:{at}\:{first}\:{the}\:{seq} \\ $$$${is}\:{either}\:{monotonic}\:{increasing}\:{or}\:{decreasing} \\ $$
Answered by Snail last updated on 21/Jul/21
$${Claim}\:{a}_{{n}+\mathrm{1}} \geqslant{a}_{{n}} \\ $$$${Go}\:{through}\:{basic}\:{steps}\:{of}\:{induction}\: \\ $$$${and}\:{then} \\ $$$${For}\:\left(\:{m}+\mathrm{1}\right)\:{case}\: \\ $$$${we}\:{have}\:\:\:\:{a}_{{m}+\mathrm{1}} \geqslant{a}_{{m}} \\ $$$$ \\ $$$$\left.\sqrt{\left(\right.}\left.{a}_{\mathrm{1}} +{a}_{{m}+\mathrm{1}} \right)\geqslant\sqrt{\left(\right.}{a}_{\mathrm{1}} +{a}_{{m}\:} \right) \\ $$$${a}_{{m}+\mathrm{2}} \geqslant{a}_{{m}} \:\:\:\:\:\:\:\:\:{hence}\:{the}\:{seq}\:{is}\:{monotonic}\:{increas} \\ $$$${Now}\:{u}\:{can}\:{do}\:{as}\:{like}\:{it}\:{is}\:{done} \\ $$
Commented by gsk2684 last updated on 21/Jul/21
$${yes}\:,\:{thank}\:{you} \\ $$
Answered by mathmax by abdo last updated on 21/Jul/21
![a_(n+1) =f(a_n ) with f(x)=(√(x+12)) (a_1 =12) f is defined continue on[−12,+∞[ f^′ (x)=(1/(2(√(x+12)))) >0 ⇒f is increazing on]−12,+∞[ so lim_(n→+∞) a_n =x_0 / f(x_0 )=x_0 (fix point of f) ⇒x_0 =(√(x_0 +12)) ⇒x_0 ^2 −x_0 −12=0 Δ=1+4(12)=49 ⇒x_1 =((1+7)/2)=4 and x_2 =((1−7)/2)=−3<0 let prove[that a_n >0 ∀n a_2 =(√(a_1 +12))>0 (true) let suppose a_n >0 ⇒ a_(n+1) =(√(a_n +12))>0 ⇒lim_(n→+∞) a_n =4](https://www.tinkutara.com/question/Q147556.png)
$$\mathrm{a}_{\mathrm{n}+\mathrm{1}} =\mathrm{f}\left(\mathrm{a}_{\mathrm{n}} \right)\:\mathrm{with}\:\mathrm{f}\left(\mathrm{x}\right)=\sqrt{\mathrm{x}+\mathrm{12}}\:\:\:\:\:\:\left(\mathrm{a}_{\mathrm{1}} =\mathrm{12}\right) \\ $$$$\mathrm{f}\:\mathrm{is}\:\mathrm{defined}\:\mathrm{continue}\:\:\mathrm{on}\left[−\mathrm{12},+\infty\left[\right.\right. \\ $$$$\left.\mathrm{f}^{'} \left(\mathrm{x}\right)=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{x}+\mathrm{12}}}\:>\mathrm{0}\:\Rightarrow\mathrm{f}\:\mathrm{is}\:\mathrm{increazing}\:\mathrm{on}\right]−\mathrm{12},+\infty\left[\right. \\ $$$$\mathrm{so}\:\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \mathrm{a}_{\mathrm{n}} =\mathrm{x}_{\mathrm{0}} \:\:\:/\:\mathrm{f}\left(\mathrm{x}_{\mathrm{0}} \right)=\mathrm{x}_{\mathrm{0}} \:\:\:\:\left(\mathrm{fix}\:\mathrm{point}\:\mathrm{of}\:\mathrm{f}\right) \\ $$$$\Rightarrow\mathrm{x}_{\mathrm{0}} =\sqrt{\mathrm{x}_{\mathrm{0}} +\mathrm{12}}\:\Rightarrow\mathrm{x}_{\mathrm{0}} ^{\mathrm{2}} −\mathrm{x}_{\mathrm{0}} −\mathrm{12}=\mathrm{0} \\ $$$$\Delta=\mathrm{1}+\mathrm{4}\left(\mathrm{12}\right)=\mathrm{49}\:\Rightarrow\mathrm{x}_{\mathrm{1}} =\frac{\mathrm{1}+\mathrm{7}}{\mathrm{2}}=\mathrm{4}\:\:\mathrm{and}\:\mathrm{x}_{\mathrm{2}} =\frac{\mathrm{1}−\mathrm{7}}{\mathrm{2}}=−\mathrm{3}<\mathrm{0} \\ $$$$\mathrm{let}\:\mathrm{prove}\left[\mathrm{that}\:\mathrm{a}_{\mathrm{n}} >\mathrm{0}\:\forall\mathrm{n}\right. \\ $$$$\mathrm{a}_{\mathrm{2}} =\sqrt{\mathrm{a}_{\mathrm{1}} +\mathrm{12}}>\mathrm{0}\:\:\left(\mathrm{true}\right)\:\mathrm{let}\:\mathrm{suppose}\:\mathrm{a}_{\mathrm{n}} >\mathrm{0}\:\Rightarrow \\ $$$$\mathrm{a}_{\mathrm{n}+\mathrm{1}} =\sqrt{\mathrm{a}_{\mathrm{n}} +\mathrm{12}}>\mathrm{0}\:\Rightarrow\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \mathrm{a}_{\mathrm{n}} =\mathrm{4} \\ $$
Commented by mathdanisur last updated on 21/Jul/21
$${thank}\:{you}\:{Sir} \\ $$