Question Number 126400 by F_Nongue last updated on 20/Dec/20
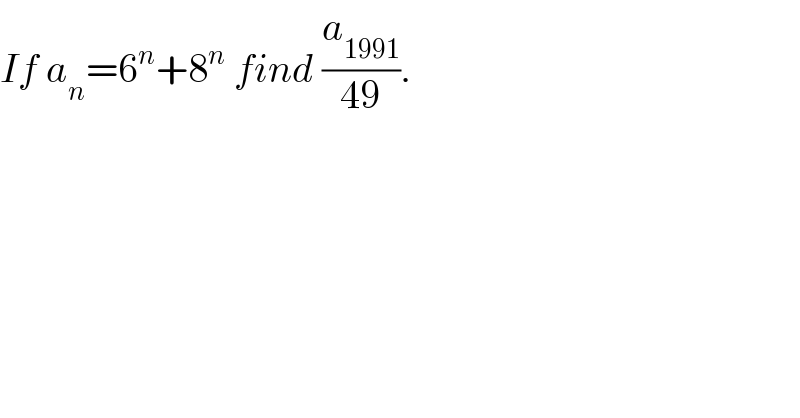
$${If}\:{a}_{{n}} =\mathrm{6}^{{n}} +\mathrm{8}^{{n}} \:{find}\:\frac{{a}_{\mathrm{1991}} }{\mathrm{49}}. \\ $$
Commented by talminator2856791 last updated on 20/Dec/20
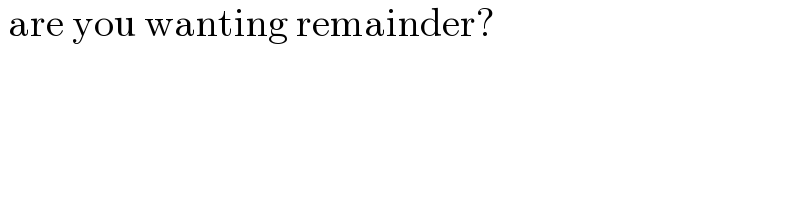
$$\:\mathrm{are}\:\mathrm{you}\:\mathrm{wanting}\:\mathrm{remainder}? \\ $$
Commented by MJS_new last updated on 20/Dec/20
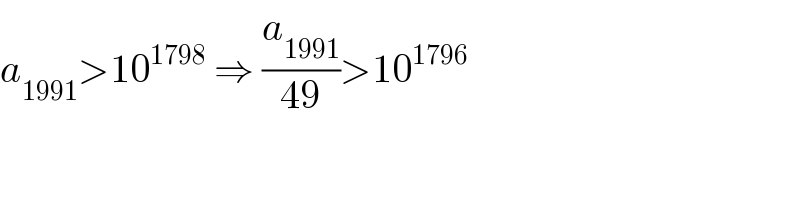
$${a}_{\mathrm{1991}} >\mathrm{10}^{\mathrm{1798}} \:\Rightarrow\:\frac{{a}_{\mathrm{1991}} }{\mathrm{49}}>\mathrm{10}^{\mathrm{1796}} \\ $$
Commented by MJS_new last updated on 20/Dec/20

$$\mathrm{the}\:\mathrm{remainder}\:\mathrm{is}\:\mathrm{42} \\ $$
Commented by F_Nongue last updated on 20/Dec/20
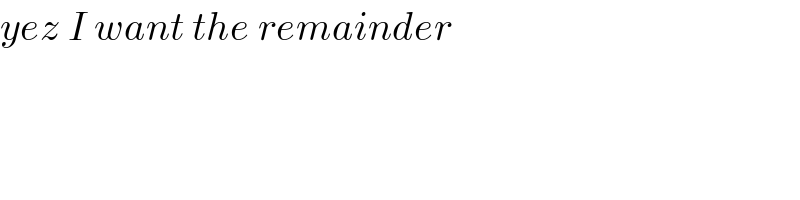
$${yez}\:{I}\:{want}\:{the}\:{remainder} \\ $$
Commented by MJS_new last updated on 20/Dec/20
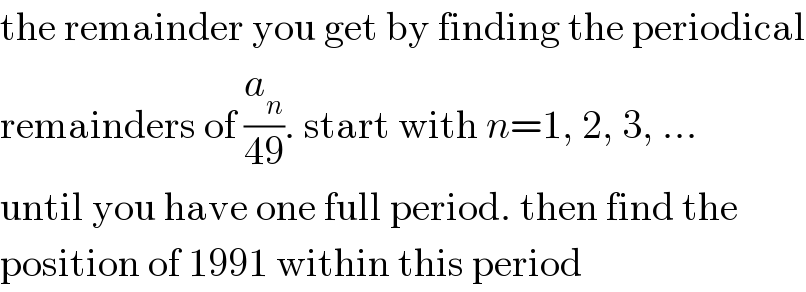
$$\mathrm{the}\:\mathrm{remainder}\:\mathrm{you}\:\mathrm{get}\:\mathrm{by}\:\mathrm{finding}\:\mathrm{the}\:\mathrm{periodical} \\ $$$$\mathrm{remainders}\:\mathrm{of}\:\frac{{a}_{{n}} }{\mathrm{49}}.\:\mathrm{start}\:\mathrm{with}\:{n}=\mathrm{1},\:\mathrm{2},\:\mathrm{3},\:… \\ $$$$\mathrm{until}\:\mathrm{you}\:\mathrm{have}\:\mathrm{one}\:\mathrm{full}\:\mathrm{period}.\:\mathrm{then}\:\mathrm{find}\:\mathrm{the} \\ $$$$\mathrm{position}\:\mathrm{of}\:\mathrm{1991}\:\mathrm{within}\:\mathrm{this}\:\mathrm{period} \\ $$
Answered by floor(10²Eta[1]) last updated on 20/Dec/20

$$\mathrm{6}^{\mathrm{1991}} +\mathrm{8}^{\mathrm{1991}} \left(\mathrm{mod}\:\mathrm{49}\right) \\ $$$$\phi\left(\mathrm{49}\right)=\mathrm{7}^{\mathrm{2}} −\mathrm{7}=\mathrm{42} \\ $$$$\mathrm{6}^{\mathrm{1991}} =\left(\mathrm{6}^{\mathrm{47}} \right)^{\mathrm{42}+\mathrm{17}} \equiv\mathrm{6}^{\mathrm{17}} \\ $$$$\mathrm{8}^{\mathrm{1991}} \equiv\mathrm{8}^{\mathrm{17}} \\ $$$$\mathrm{a}_{\mathrm{1991}} \equiv\mathrm{6}^{\mathrm{17}} +\mathrm{8}^{\mathrm{17}} \left(\mathrm{mod}\:\mathrm{49}\right) \\ $$$$\mathrm{6}^{\mathrm{2}} =\mathrm{36}\equiv−\mathrm{13}\left(\mathrm{mod}\:\mathrm{49}\right) \\ $$$$\mathrm{6}^{\mathrm{17}} =\left(\mathrm{6}^{\mathrm{2}} \right)^{\mathrm{8}} .\mathrm{6}\equiv\mathrm{13}^{\mathrm{8}} .\mathrm{6}=\left(\mathrm{13}^{\mathrm{2}} \right)^{\mathrm{4}} .\mathrm{6}\equiv\mathrm{22}^{\mathrm{4}} .\mathrm{6} \\ $$$$\equiv\left(\mathrm{22}^{\mathrm{2}} \right)^{\mathrm{2}} .\mathrm{6}\equiv\left(−\mathrm{6}\right)^{\mathrm{2}} .\mathrm{6}\equiv\mathrm{6}^{\mathrm{2}} .\mathrm{6}\equiv−\mathrm{13}.\mathrm{6}\equiv−\mathrm{78}\equiv\mathrm{20}\left(\mathrm{mod}\:\mathrm{49}\right) \\ $$$$\mathrm{8}^{\mathrm{2}} =\mathrm{64}\equiv\mathrm{15}\left(\mathrm{mod}\:\mathrm{49}\right) \\ $$$$\mathrm{8}^{\mathrm{17}} \equiv\left(\mathrm{8}^{\mathrm{2}} \right)^{\mathrm{8}} .\mathrm{8}\equiv\mathrm{15}^{\mathrm{8}} .\mathrm{8}=\left(\mathrm{15}^{\mathrm{2}} \right)^{\mathrm{4}} .\mathrm{8}\equiv\left(−\mathrm{20}\right)^{\mathrm{4}} .\mathrm{8}=\mathrm{20}^{\mathrm{4}} .\mathrm{8} \\ $$$$=\left(\mathrm{20}^{\mathrm{2}} \right)^{\mathrm{2}} .\mathrm{8}\equiv\mathrm{8}^{\mathrm{2}} .\mathrm{8}\equiv\mathrm{15}.\mathrm{8}\equiv\mathrm{22}\left(\mathrm{mod}\:\mathrm{49}\right) \\ $$$$\mathrm{a}_{\mathrm{1991}} \equiv\mathrm{20}+\mathrm{22}\equiv\mathrm{42}\left(\mathrm{mod49}\right) \\ $$$$ \\ $$
