Question Number 63054 by jimful last updated on 28/Jun/19
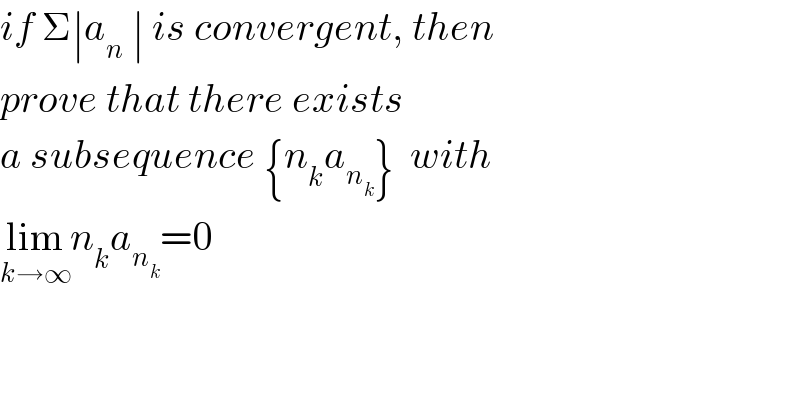
$${if}\:\Sigma\mid{a}_{{n}} \:\mid\:{is}\:{convergent},\:{then} \\ $$$${prove}\:{that}\:{there}\:{exists}\: \\ $$$${a}\:{subsequence}\:\left\{{n}_{{k}} {a}_{{n}_{{k}} } \right\}\:\:{with} \\ $$$$\underset{{k}\rightarrow\infty} {\mathrm{lim}}{n}_{{k}} {a}_{{n}_{{k}} } =\mathrm{0} \\ $$
