Question Number 63466 by vajpaithegrate@gmail.com last updated on 04/Jul/19
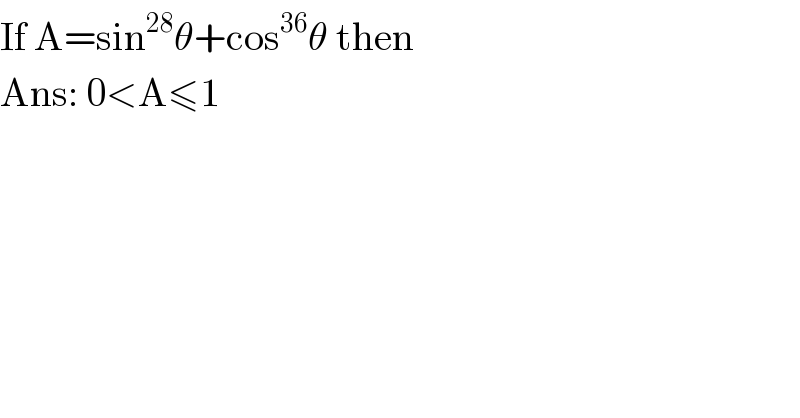
$$\mathrm{If}\:\mathrm{A}=\mathrm{sin}^{\mathrm{28}} \theta+\mathrm{cos}^{\mathrm{36}} \theta\:\mathrm{then} \\ $$$$\mathrm{Ans}:\:\mathrm{0}<\mathrm{A}\leqslant\mathrm{1} \\ $$
Commented by MJS last updated on 05/Jul/19
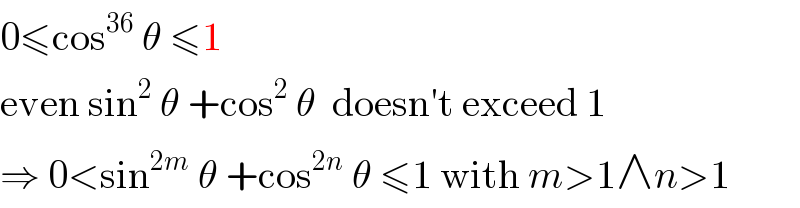
$$\mathrm{0}\leqslant\mathrm{cos}^{\mathrm{36}} \:\theta\:\leqslant\mathrm{1} \\ $$$$\mathrm{even}\:\mathrm{sin}^{\mathrm{2}} \:\theta\:+\mathrm{cos}^{\mathrm{2}} \:\theta\:\:\mathrm{doesn}'\mathrm{t}\:\mathrm{exceed}\:\mathrm{1} \\ $$$$\Rightarrow\:\mathrm{0}<\mathrm{sin}^{\mathrm{2}{m}} \:\theta\:+\mathrm{cos}^{\mathrm{2}{n}} \:\theta\:\leqslant\mathrm{1}\:\mathrm{with}\:{m}>\mathrm{1}\wedge{n}>\mathrm{1} \\ $$
Commented by Prithwish sen last updated on 05/Jul/19
![−1≤ sinθ≤ 1 and −1≤ cosθ ≤ 1 or, 0≤ sin^(28) θ ≤1 and 0≤ cos^(36) θ ≤ 1 ∵ sin^(28) θ ≠ cos^(36) θ ∀ θ ∈ [−∞,∞] ∴ 0<sin^(28) θ + cos^(36) θ≤ 1 please check.](https://www.tinkutara.com/question/Q63486.png)
$$\:−\mathrm{1}\leqslant\:\mathrm{sin}\theta\leqslant\:\mathrm{1}\:\:\:\:\mathrm{and}\:\:−\mathrm{1}\leqslant\:\mathrm{cos}\theta\:\leqslant\:\mathrm{1} \\ $$$$\:\mathrm{or},\:\mathrm{0}\leqslant\:\mathrm{sin}^{\mathrm{28}} \theta\:\leqslant\mathrm{1}\:\:\:\mathrm{and}\:\mathrm{0}\leqslant\:\mathrm{cos}^{\mathrm{36}} \theta\:\leqslant\:\mathrm{1} \\ $$$$\because\:\mathrm{sin}^{\mathrm{28}} \theta\:\neq\:\mathrm{cos}^{\mathrm{36}} \theta\:\:\forall\:\theta\:\in\:\left[−\infty,\infty\right] \\ $$$$\therefore\:\mathrm{0}<\mathrm{sin}^{\mathrm{28}} \theta\:+\:\mathrm{cos}^{\mathrm{36}} \theta\leqslant\:\mathrm{1} \\ $$$$\mathrm{please}\:\mathrm{check}. \\ $$
Commented by vajpaithegrate@gmail.com last updated on 05/Jul/19

$$\mathrm{tnq}\:\mathrm{sir} \\ $$
Commented by Prithwish sen last updated on 05/Jul/19
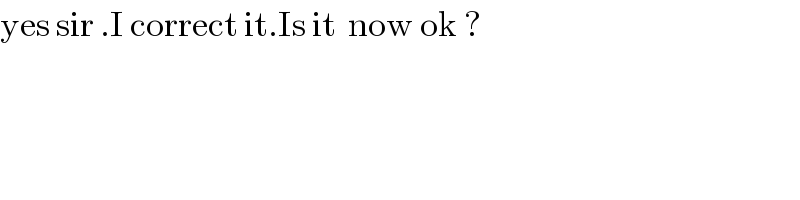
$$\mathrm{yes}\:\mathrm{sir}\:.\mathrm{I}\:\mathrm{correct}\:\mathrm{it}.\mathrm{Is}\:\mathrm{it}\:\:\mathrm{now}\:\mathrm{ok}\:? \\ $$
Commented by Prithwish sen last updated on 05/Jul/19
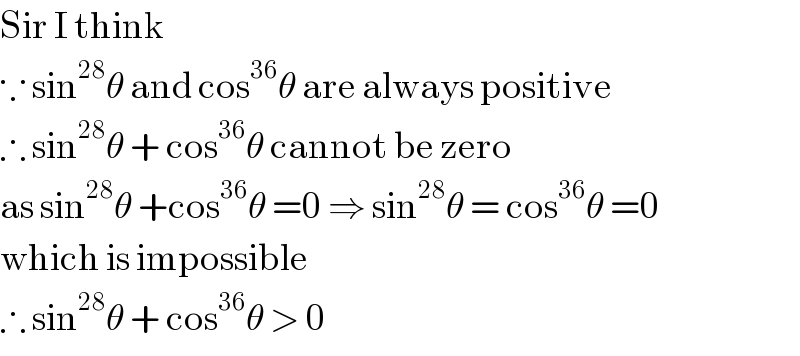
$$\mathrm{Sir}\:\mathrm{I}\:\mathrm{think}\: \\ $$$$\because\:\mathrm{sin}^{\mathrm{28}} \theta\:\mathrm{and}\:\mathrm{cos}^{\mathrm{36}} \theta\:\mathrm{are}\:\mathrm{always}\:\mathrm{positive} \\ $$$$\therefore\:\mathrm{sin}^{\mathrm{28}} \theta\:+\:\mathrm{cos}^{\mathrm{36}} \theta\:\mathrm{cannot}\:\mathrm{be}\:\mathrm{zero} \\ $$$$\mathrm{as}\:\mathrm{sin}^{\mathrm{28}} \theta\:+\mathrm{cos}^{\mathrm{36}} \theta\:=\mathrm{0}\:\Rightarrow\:\mathrm{sin}^{\mathrm{28}} \theta\:=\:\mathrm{cos}^{\mathrm{36}} \theta\:=\mathrm{0} \\ $$$$\mathrm{which}\:\mathrm{is}\:\mathrm{impossible} \\ $$$$\therefore\:\mathrm{sin}^{\mathrm{28}} \theta\:+\:\mathrm{cos}^{\mathrm{36}} \theta\:>\:\mathrm{0} \\ $$
Commented by MJS last updated on 05/Jul/19
$$\mathrm{you}'\mathrm{re}\:\mathrm{right} \\ $$$$\mathrm{but}\:\mathrm{above}\:\mathrm{there}'\mathrm{s}\:\mathrm{still}\:\mathrm{a}\:\mathrm{typo}\:\mathrm{in}\:\mathrm{your}\:\mathrm{first} \\ $$$$\mathrm{comment}:\:\mathrm{it}\:\mathrm{must}\:\mathrm{be}\:\mathrm{0}<…\leqslant\mathrm{1} \\ $$
Commented by Prithwish sen last updated on 05/Jul/19
$$\mathrm{Thankyou}\:\mathrm{very}\:\mathrm{much}\:\mathrm{sir}. \\ $$
