If-a-x-9-x-9-a-7-find-a-x-9-1-4-x-9-a-1-4-

Question Number 182530 by HeferH last updated on 10/Dec/22

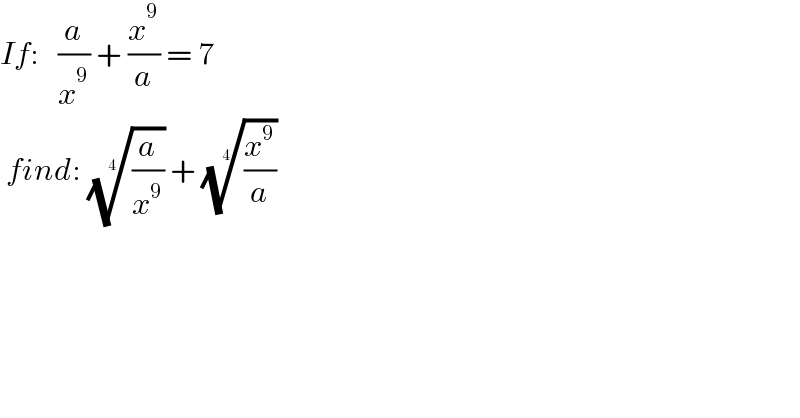
$${If}:\:\:\:\frac{{a}}{{x}^{\mathrm{9}} }\:+\:\frac{{x}^{\mathrm{9}} }{{a}}\:=\:\mathrm{7} \\ $$$$\:{find}:\:\sqrt[{\mathrm{4}}]{\frac{{a}}{{x}^{\mathrm{9}} }}\:+\:\sqrt[{\mathrm{4}}]{\frac{{x}^{\mathrm{9}} }{{a}}} \\ $$

Answered by mr W last updated on 10/Dec/22

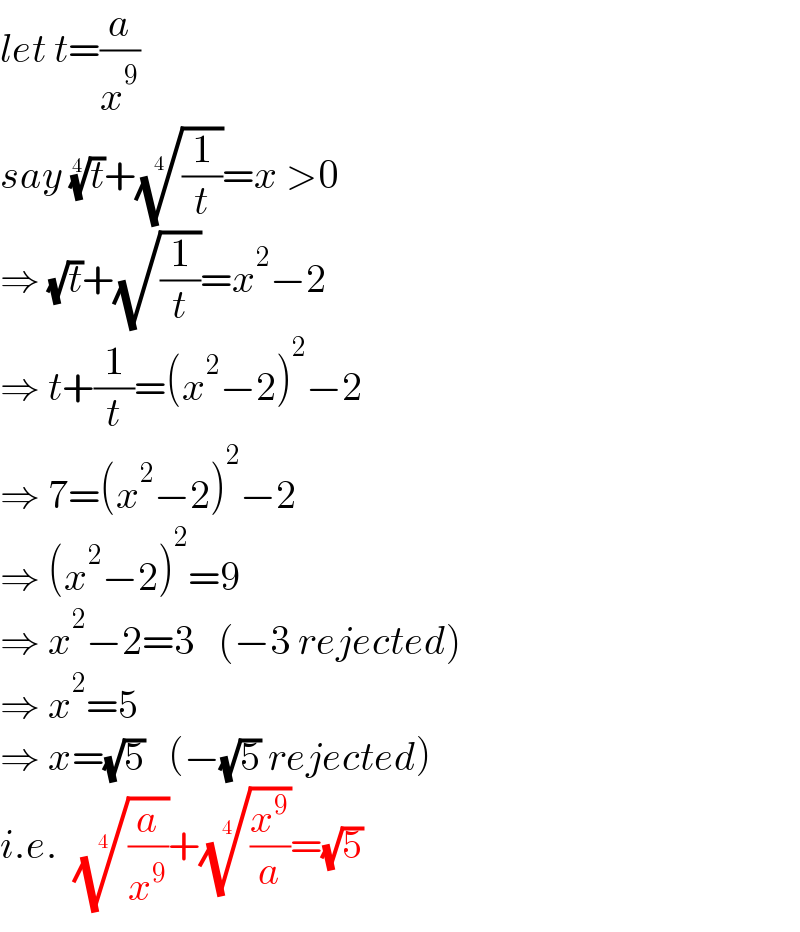
let t=(a/x^9 ) say (t)^(1/4) +((1/t))^(1/4) =x >0 ⇒ (√t)+(√(1/t))=x^2 −2 ⇒ t+(1/t)=(x^2 −2)^2 −2 ⇒ 7=(x^2 −2)^2 −2 ⇒ (x^2 −2)^2 =9 ⇒ x^2 −2=3 (−3 rejected) ⇒ x^2 =5 ⇒ x=(√5) (−(√5) rejected) i.e. ((a/x^9 ))^(1/4) +((x^9 /a))^(1/4) =(√5)

$${let}\:{t}=\frac{{a}}{{x}^{\mathrm{9}} } \\ $$$${say}\:\sqrt[{\mathrm{4}}]{{t}}+\sqrt[{\mathrm{4}}]{\frac{\mathrm{1}}{{t}}}={x}\:>\mathrm{0} \\ $$$$\Rightarrow\:\sqrt{{t}}+\sqrt{\frac{\mathrm{1}}{{t}}}={x}^{\mathrm{2}} −\mathrm{2} \\ $$$$\Rightarrow\:{t}+\frac{\mathrm{1}}{{t}}=\left({x}^{\mathrm{2}} −\mathrm{2}\right)^{\mathrm{2}} −\mathrm{2} \\ $$$$\Rightarrow\:\mathrm{7}=\left({x}^{\mathrm{2}} −\mathrm{2}\right)^{\mathrm{2}} −\mathrm{2} \\ $$$$\Rightarrow\:\left({x}^{\mathrm{2}} −\mathrm{2}\right)^{\mathrm{2}} =\mathrm{9} \\ $$$$\Rightarrow\:{x}^{\mathrm{2}} −\mathrm{2}=\mathrm{3}\:\:\:\left(−\mathrm{3}\:{rejected}\right) \\ $$$$\Rightarrow\:{x}^{\mathrm{2}} =\mathrm{5} \\ $$$$\Rightarrow\:{x}=\sqrt{\mathrm{5}}\:\:\:\left(−\sqrt{\mathrm{5}}\:{rejected}\right) \\ $$$${i}.{e}.\:\:\sqrt[{\mathrm{4}}]{\frac{{a}}{{x}^{\mathrm{9}} }}+\sqrt[{\mathrm{4}}]{\frac{{x}^{\mathrm{9}} }{{a}}}=\sqrt{\mathrm{5}} \\ $$

Answered by Frix last updated on 10/Dec/22

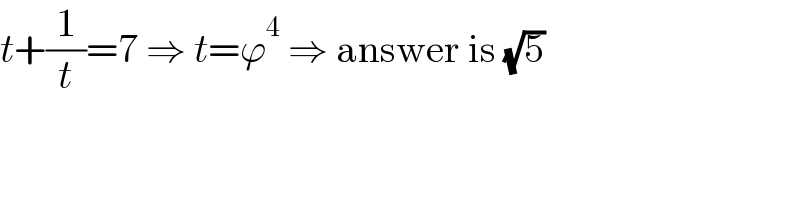
$${t}+\frac{\mathrm{1}}{{t}}=\mathrm{7}\:\Rightarrow\:{t}=\varphi^{\mathrm{4}} \:\Rightarrow\:\mathrm{answer}\:\mathrm{is}\:\sqrt{\mathrm{5}} \\ $$

Commented by manxsol last updated on 11/Dec/22

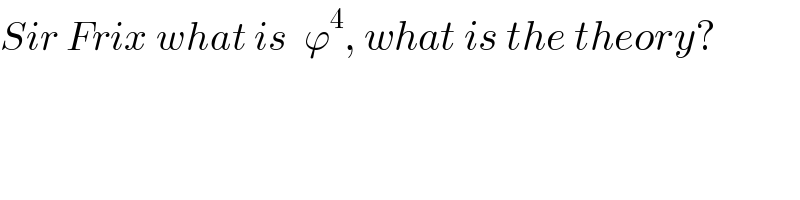
Sir Frix what is ϕ^4 , what is the theory?

$${Sir}\:{Frix}\:{what}\:{is}\:\:\varphi^{\mathrm{4}} ,\:{what}\:{is}\:{the}\:{theory}? \\ $$

Commented by Frix last updated on 11/Dec/22

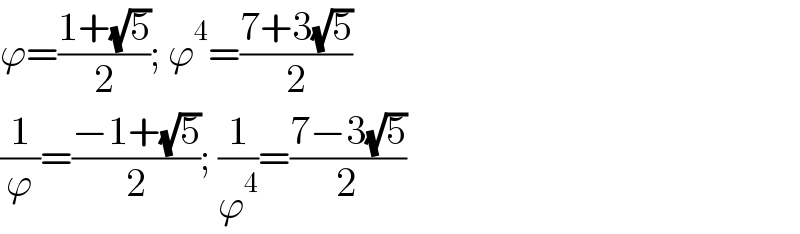
ϕ=((1+(√5))/2); ϕ^4 =((7+3(√5))/2) (1/ϕ)=((−1+(√5))/2); (1/ϕ^4 )=((7−3(√5))/2)

$$\varphi=\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}};\:\varphi^{\mathrm{4}} =\frac{\mathrm{7}+\mathrm{3}\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$$\frac{\mathrm{1}}{\varphi}=\frac{−\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}};\:\frac{\mathrm{1}}{\varphi^{\mathrm{4}} }=\frac{\mathrm{7}−\mathrm{3}\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$

Commented by manxsol last updated on 12/Dec/22

$${thanks},{Sir}\:{Frix}\:{is}\:{golden}\:{number}.\:{check}\:{my}\:{next}\:{question} \\ $$

Answered by Ar Brandon last updated on 11/Dec/22

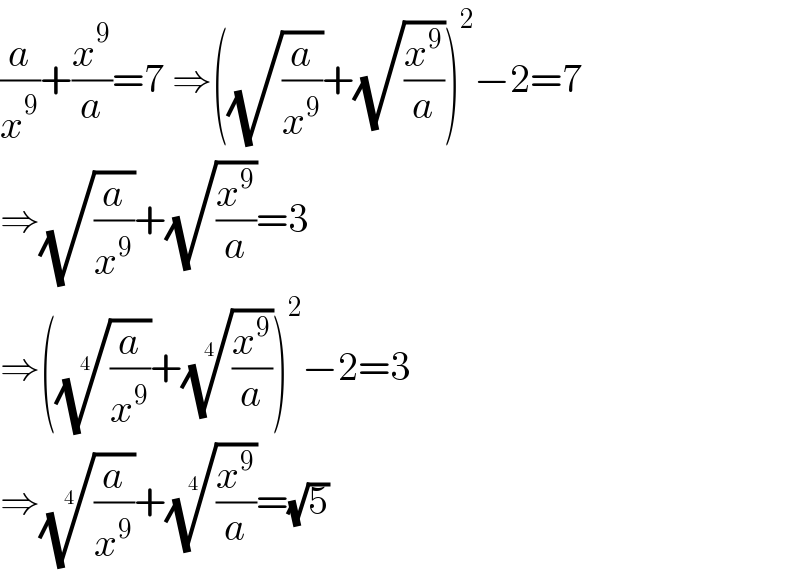
(a/x^9 )+(x^9 /a)=7 ⇒((√(a/x^9 ))+(√(x^9 /a)))^2 −2=7 ⇒(√(a/x^9 ))+(√(x^9 /a))=3 ⇒(((a/x^9 ))^(1/4) +((x^9 /a))^(1/4) )^2 −2=3 ⇒((a/x^9 ))^(1/4) +((x^9 /a))^(1/4) =(√5)

$$\frac{{a}}{{x}^{\mathrm{9}} }+\frac{{x}^{\mathrm{9}} }{{a}}=\mathrm{7}\:\Rightarrow\left(\sqrt{\frac{{a}}{{x}^{\mathrm{9}} }}+\sqrt{\frac{{x}^{\mathrm{9}} }{{a}}}\right)^{\mathrm{2}} −\mathrm{2}=\mathrm{7} \\ $$$$\Rightarrow\sqrt{\frac{{a}}{{x}^{\mathrm{9}} }}+\sqrt{\frac{{x}^{\mathrm{9}} }{{a}}}=\mathrm{3} \\ $$$$\Rightarrow\left(\sqrt[{\mathrm{4}}]{\frac{{a}}{{x}^{\mathrm{9}} }}+\sqrt[{\mathrm{4}}]{\frac{{x}^{\mathrm{9}} }{{a}}}\right)^{\mathrm{2}} −\mathrm{2}=\mathrm{3} \\ $$$$\Rightarrow\sqrt[{\mathrm{4}}]{\frac{{a}}{{x}^{\mathrm{9}} }}+\sqrt[{\mathrm{4}}]{\frac{{x}^{\mathrm{9}} }{{a}}}=\sqrt{\mathrm{5}} \\ $$

Facebook Tweet Pin

If-a-x-9-x-9-a-7-find-a-x-9-1-4-x-9-a-1-4-

Leave a Reply Cancel reply