Menu Close

If-acosh-x-bsinh-x-c-show-that-x-ln-c-c-2-b-2-a-2-a-b-

Tinku Tara 0 Comments
Pin




Question Number 178415 by Spillover last updated on 16/Oct/22
If acosh x+bsinh x=c show that. x=ln [((c±(√(c^2 +b^2 −a^2 )))/(a+b))]
$$\mathrm{If}\:\mathrm{acosh}\:\mathrm{x}+\mathrm{bsinh}\:\mathrm{x}=\mathrm{c}\: \\ $$$$\mathrm{show}\:\mathrm{that}. \\ $$$$\mathrm{x}=\mathrm{ln}\:\left[\frac{\mathrm{c}\pm\sqrt{\mathrm{c}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} −\mathrm{a}^{\mathrm{2}} }}{\mathrm{a}+\mathrm{b}}\right] \\ $$
Answered by haladu last updated on 16/Oct/22
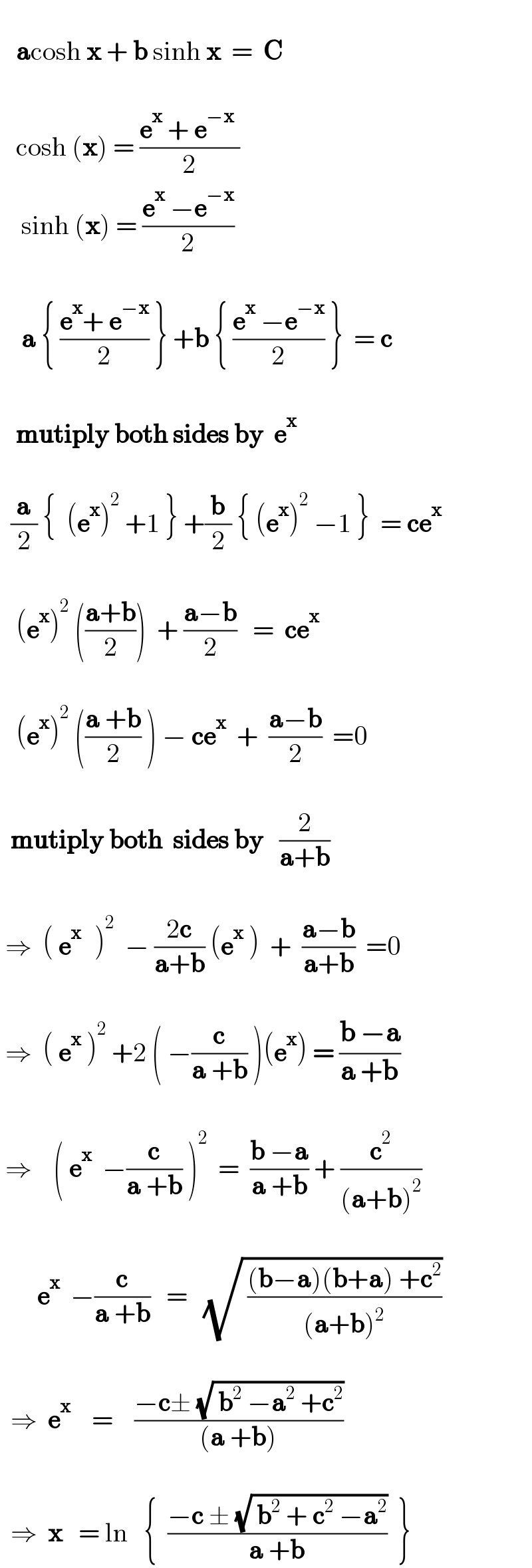
acosh x + b sinh x = C cosh (x) = ((e^x + e^(−x) )/2) sinh (x) = ((e^x −e^(−x) )/2) a { ((e^x + e^(−x) )/2) } +b { ((e^x −e^(−x) )/2) } = c mutiply both sides by e^x (a/2) { (e^x )^2 +1 } +(b/2) { (e^x )^2 −1 } = ce^x (e^x )^2 (((a+b)/2)) + ((a−b)/2) = ce^x (e^x )^2 (((a +b)/2) ) − ce^x + ((a−b)/2) =0 mutiply both sides by (2/(a+b)) ⇒ ( e^(x ) )^2 − ((2c)/(a+b)) (e^x ) + ((a−b)/(a+b)) =0 ⇒ ( e^x )^2 +2 ( −(c/(a +b)) )(e^x ) = ((b −a)/(a +b)) ⇒ ( e^x −(c/(a +b)) )^2 = ((b −a)/(a +b)) + (c^2 /((a+b)^2 )) e^x −(c/(a +b)) = (√( (((b−a)(b+a) +c^2 )/((a+b)^2 )))) ⇒ e^x = ((−c± (√( b^2 −a^2 +c^2 )))/((a +b))) ⇒ x = ln { ((−c ± (√( b^2 + c^2 −a^2 )))/(a +b)) }
$$ \\ $$$$\:\:\:\boldsymbol{\mathrm{a}}\mathrm{cosh}\:\boldsymbol{\mathrm{x}}\:+\:\boldsymbol{\mathrm{b}}\:\mathrm{sinh}\:\boldsymbol{\mathrm{x}}\:\:=\:\:\boldsymbol{\mathrm{C}} \\ $$$$\:\:\: \\ $$$$\:\:\:\mathrm{cosh}\:\left(\boldsymbol{\mathrm{x}}\right)\:=\:\frac{\boldsymbol{\mathrm{e}}^{\boldsymbol{\mathrm{x}}} \:+\:\boldsymbol{\mathrm{e}}^{−\boldsymbol{\mathrm{x}}} \:}{\mathrm{2}} \\ $$$$\:\:\:\:\mathrm{sinh}\:\left(\boldsymbol{\mathrm{x}}\right)\:=\:\frac{\boldsymbol{\mathrm{e}}^{\boldsymbol{\mathrm{x}}} \:−\boldsymbol{\mathrm{e}}^{−\boldsymbol{\mathrm{x}}} }{\mathrm{2}} \\ $$$$\:\:\:\: \\ $$$$\:\:\:\:\boldsymbol{\mathrm{a}}\:\left\{\:\frac{\boldsymbol{\mathrm{e}}^{\boldsymbol{\mathrm{x}}} +\:\boldsymbol{\mathrm{e}}^{−\boldsymbol{\mathrm{x}}} }{\mathrm{2}}\:\right\}\:+\boldsymbol{\mathrm{b}}\:\left\{\:\frac{\boldsymbol{\mathrm{e}}^{\boldsymbol{\mathrm{x}}} \:−\boldsymbol{\mathrm{e}}^{−\boldsymbol{\mathrm{x}}} }{\mathrm{2}}\:\right\}\:\:=\:\boldsymbol{\mathrm{c}} \\ $$$$\:\:\: \\ $$$$\:\:\:\boldsymbol{\mathrm{mutiply}}\:\boldsymbol{\mathrm{both}}\:\boldsymbol{\mathrm{sides}}\:\boldsymbol{\mathrm{by}}\:\:\boldsymbol{\mathrm{e}}^{\boldsymbol{\mathrm{x}}} \:\: \\ $$$$\:\:\: \\ $$$$\:\:\frac{\boldsymbol{\mathrm{a}}}{\mathrm{2}}\:\left\{\:\:\left(\boldsymbol{\mathrm{e}}^{\boldsymbol{\mathrm{x}}} \right)^{\mathrm{2}} \:+\mathrm{1}\:\right\}\:+\frac{\boldsymbol{\mathrm{b}}}{\mathrm{2}}\:\left\{\:\left(\boldsymbol{\mathrm{e}}^{\boldsymbol{\mathrm{x}}} \right)^{\mathrm{2}} \:−\mathrm{1}\:\right\}\:\:=\:\boldsymbol{\mathrm{ce}}^{\boldsymbol{\mathrm{x}}} \\ $$$$\:\:\:\:\: \\ $$$$\:\:\:\left(\boldsymbol{\mathrm{e}}^{\boldsymbol{\mathrm{x}}} \right)^{\mathrm{2}} \:\left(\frac{\boldsymbol{\mathrm{a}}+\boldsymbol{\mathrm{b}}}{\mathrm{2}}\right)\:\:+\:\frac{\boldsymbol{\mathrm{a}}−\boldsymbol{\mathrm{b}}}{\mathrm{2}}\:\:\:=\:\:\boldsymbol{\mathrm{ce}}^{\boldsymbol{\mathrm{x}}} \:\: \\ $$$$\:\:\:\: \\ $$$$\:\:\:\left(\boldsymbol{\mathrm{e}}^{\boldsymbol{\mathrm{x}}} \right)^{\mathrm{2}} \:\left(\frac{\boldsymbol{\mathrm{a}}\:+\boldsymbol{\mathrm{b}}}{\mathrm{2}}\:\right)\:−\:\boldsymbol{\mathrm{ce}}^{\boldsymbol{\mathrm{x}}} \:\:+\:\:\frac{\boldsymbol{\mathrm{a}}−\boldsymbol{\mathrm{b}}}{\mathrm{2}}\:\:=\mathrm{0} \\ $$$$\:\:\: \\ $$$$\:\:\boldsymbol{\mathrm{mutiply}}\:\boldsymbol{\mathrm{both}}\:\:\boldsymbol{\mathrm{sides}}\:\boldsymbol{\mathrm{by}}\:\:\:\frac{\mathrm{2}}{\boldsymbol{\mathrm{a}}+\boldsymbol{\mathrm{b}}} \\ $$$$\:\: \\ $$$$\:\Rightarrow\:\:\left(\:\boldsymbol{\mathrm{e}}^{\boldsymbol{\mathrm{x}}\:} \:\:\right)^{\mathrm{2}} \:\:−\:\frac{\mathrm{2}\boldsymbol{\mathrm{c}}}{\boldsymbol{\mathrm{a}}+\boldsymbol{\mathrm{b}}}\:\left(\boldsymbol{\mathrm{e}}^{\boldsymbol{\mathrm{x}}} \:\right)\:\:+\:\:\frac{\boldsymbol{\mathrm{a}}−\boldsymbol{\mathrm{b}}}{\boldsymbol{\mathrm{a}}+\boldsymbol{\mathrm{b}}}\:\:=\mathrm{0} \\ $$$$\:\:\: \\ $$$$\:\Rightarrow\:\:\left(\:\boldsymbol{\mathrm{e}}^{\boldsymbol{\mathrm{x}}} \:\right)^{\mathrm{2}} \:+\mathrm{2}\:\left(\:−\frac{\boldsymbol{\mathrm{c}}}{\boldsymbol{\mathrm{a}}\:+\boldsymbol{\mathrm{b}}}\:\right)\left(\boldsymbol{\mathrm{e}}^{\boldsymbol{\mathrm{x}}} \right)\:=\:\frac{\boldsymbol{\mathrm{b}}\:−\boldsymbol{\mathrm{a}}}{\boldsymbol{\mathrm{a}}\:+\boldsymbol{\mathrm{b}}}\:\: \\ $$$$\:\:\: \\ $$$$\:\Rightarrow\:\:\:\:\left(\:\boldsymbol{\mathrm{e}}^{\boldsymbol{\mathrm{x}}} \:\:−\frac{\boldsymbol{\mathrm{c}}}{\boldsymbol{\mathrm{a}}\:+\boldsymbol{\mathrm{b}}}\:\right)^{\mathrm{2}} \:\:=\:\:\frac{\boldsymbol{\mathrm{b}}\:−\boldsymbol{\mathrm{a}}}{\boldsymbol{\mathrm{a}}\:+\boldsymbol{\mathrm{b}}}\:+\:\frac{\boldsymbol{\mathrm{c}}^{\mathrm{2}} }{\left(\boldsymbol{\mathrm{a}}+\boldsymbol{\mathrm{b}}\right)^{\mathrm{2}} } \\ $$$$\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\boldsymbol{\mathrm{e}}^{\boldsymbol{\mathrm{x}}} \:\:−\frac{\boldsymbol{\mathrm{c}}}{\boldsymbol{\mathrm{a}}\:+\boldsymbol{\mathrm{b}}}\:\:\:=\:\:\:\sqrt{\:\frac{\left(\boldsymbol{\mathrm{b}}−\boldsymbol{\mathrm{a}}\right)\left(\boldsymbol{\mathrm{b}}+\boldsymbol{\mathrm{a}}\right)\:+\boldsymbol{\mathrm{c}}^{\mathrm{2}} }{\left(\boldsymbol{\mathrm{a}}+\boldsymbol{\mathrm{b}}\right)^{\mathrm{2}} }} \\ $$$$\:\:\:\:\: \\ $$$$\:\:\Rightarrow\:\:\boldsymbol{\mathrm{e}}^{\boldsymbol{\mathrm{x}}} \:\:\:\:=\:\:\:\:\frac{−\boldsymbol{\mathrm{c}}\pm\:\sqrt{\:\boldsymbol{\mathrm{b}}^{\mathrm{2}} \:−\boldsymbol{\mathrm{a}}^{\mathrm{2}} \:+\boldsymbol{\mathrm{c}}^{\mathrm{2}} }}{\left(\boldsymbol{\mathrm{a}}\:+\boldsymbol{\mathrm{b}}\right)} \\ $$$$\:\:\:\: \\ $$$$\:\:\Rightarrow\:\:\boldsymbol{\mathrm{x}}\:\:\:=\:\mathrm{ln}\:\:\:\left\{\:\:\frac{−\boldsymbol{\mathrm{c}}\:\pm\:\sqrt{\:\boldsymbol{\mathrm{b}}^{\mathrm{2}} \:+\:\boldsymbol{\mathrm{c}}^{\mathrm{2}} \:−\boldsymbol{\mathrm{a}}^{\mathrm{2}} }}{\boldsymbol{\mathrm{a}}\:+\boldsymbol{\mathrm{b}}}\:\:\right\}\: \\ $$
Commented by Spillover last updated on 16/Oct/22
thank you
$${thank}\:{you} \\ $$
Commented by haladu last updated on 16/Oct/22
You are wellcome
$$\: \\ $$$$\:\:\boldsymbol{\mathrm{You}}\:\boldsymbol{\mathrm{are}}\:\boldsymbol{\mathrm{wellcome}}\: \\ $$
Answered by CElcedricjunior last updated on 16/Oct/22
on acoshx+bsinhx=c =>acoshx+bsinhx=a(((e^x +e^(−x) )/2))+b(((e^x −e^(−x) )/2)) = =>(a+b)e^(2x) +(a−b)−2ce^x =0 =>Δ=4c^2 −4(a^2 −b^2 ) supposons que 𝚫>0 ie c^2 >a^2 −b^2 =>𝚫=2(√(c^2 +b^2 −a^2 )) =>e^x =((c∓(√(c^2 +b^2 −a^2 )))/(a+b)) =>x=ln∣((c∓(√(c^2 +b^2 −c)))/(a+b))∣ ............le celebre cedric junior.......
$$\boldsymbol{\mathrm{on}}\:\boldsymbol{\mathrm{acoshx}}+\boldsymbol{\mathrm{bsinhx}}=\boldsymbol{\mathrm{c}} \\ $$$$=>\boldsymbol{\mathrm{acoshx}}+\boldsymbol{\mathrm{bsinhx}}=\boldsymbol{\mathrm{a}}\left(\frac{\boldsymbol{\mathrm{e}}^{\boldsymbol{\mathrm{x}}} +\boldsymbol{\mathrm{e}}^{−\boldsymbol{\mathrm{x}}} }{\mathrm{2}}\right)+\boldsymbol{\mathrm{b}}\left(\frac{\boldsymbol{\mathrm{e}}^{\boldsymbol{\mathrm{x}}} −\boldsymbol{\mathrm{e}}^{−\boldsymbol{\mathrm{x}}} }{\mathrm{2}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:= \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=>\left(\boldsymbol{\mathrm{a}}+\boldsymbol{\mathrm{b}}\right)\boldsymbol{\mathrm{e}}^{\mathrm{2}\boldsymbol{\mathrm{x}}} +\left(\boldsymbol{\mathrm{a}}−\boldsymbol{\mathrm{b}}\right)−\mathrm{2}\boldsymbol{\mathrm{ce}}^{\boldsymbol{\mathrm{x}}} =\mathrm{0} \\ $$$$=>\Delta=\mathrm{4}\boldsymbol{\mathrm{c}}^{\mathrm{2}} −\mathrm{4}\left(\boldsymbol{\mathrm{a}}^{\mathrm{2}} −\boldsymbol{\mathrm{b}}^{\mathrm{2}} \right) \\ $$$$\boldsymbol{\mathrm{supposons}}\:\boldsymbol{\mathrm{que}}\:\boldsymbol{\Delta}>\mathrm{0}\:\boldsymbol{\mathrm{ie}}\:\boldsymbol{\mathrm{c}}^{\mathrm{2}} >\boldsymbol{\mathrm{a}}^{\mathrm{2}} −\boldsymbol{\mathrm{b}}^{\mathrm{2}} =>\boldsymbol{\Delta}=\mathrm{2}\sqrt{\boldsymbol{\mathrm{c}}^{\mathrm{2}} +\boldsymbol{\mathrm{b}}^{\mathrm{2}} −\boldsymbol{\mathrm{a}}^{\mathrm{2}} } \\ $$$$=>\boldsymbol{\mathrm{e}}^{\boldsymbol{\mathrm{x}}} =\frac{\boldsymbol{\mathrm{c}}\mp\sqrt{\boldsymbol{\mathrm{c}}^{\mathrm{2}} +\boldsymbol{\mathrm{b}}^{\mathrm{2}} −\boldsymbol{\mathrm{a}}^{\mathrm{2}} }}{\boldsymbol{\mathrm{a}}+\boldsymbol{\mathrm{b}}} \\ $$$$=>\boldsymbol{\mathrm{x}}=\boldsymbol{\mathrm{ln}}\mid\frac{\boldsymbol{\mathrm{c}}\mp\sqrt{\boldsymbol{\mathrm{c}}^{\mathrm{2}} +\boldsymbol{\mathrm{b}}^{\mathrm{2}} −\boldsymbol{\mathrm{c}}}}{\boldsymbol{\mathrm{a}}+\boldsymbol{\mathrm{b}}}\mid \\ $$$$\: \\ $$$$…………{le}\:{celebre}\:{cedric}\:{junior}……. \\ $$
Commented by Spillover last updated on 16/Oct/22
thanks
$${thanks} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *