Question Number 167985 by peter frank last updated on 31/Mar/22
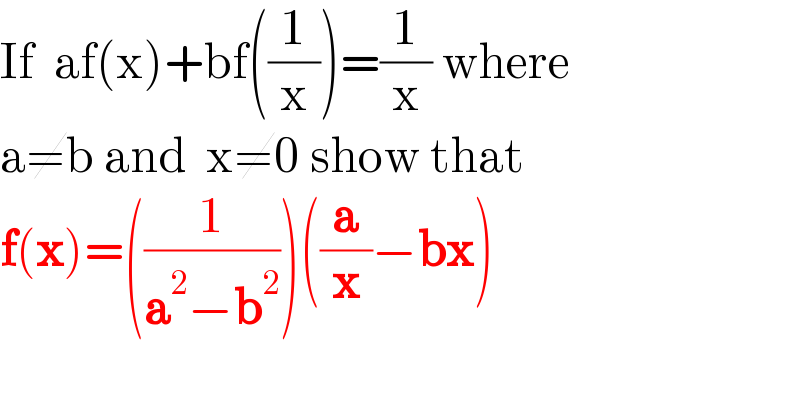
$$\mathrm{If}\:\:\mathrm{af}\left(\mathrm{x}\right)+\mathrm{bf}\left(\frac{\mathrm{1}}{\mathrm{x}}\right)=\frac{\mathrm{1}}{\mathrm{x}}\:\mathrm{where}\: \\ $$$$\mathrm{a}\neq\mathrm{b}\:\mathrm{and}\:\:\mathrm{x}\neq\mathrm{0}\:\mathrm{show}\:\mathrm{that} \\ $$$$\boldsymbol{\mathrm{f}}\left(\boldsymbol{\mathrm{x}}\right)=\left(\frac{\mathrm{1}}{\boldsymbol{\mathrm{a}}^{\mathrm{2}} −\boldsymbol{\mathrm{b}}^{\mathrm{2}} }\right)\left(\frac{\boldsymbol{\mathrm{a}}}{\boldsymbol{\mathrm{x}}}−\boldsymbol{\mathrm{bx}}\right) \\ $$
Answered by som(math1967) last updated on 31/Mar/22
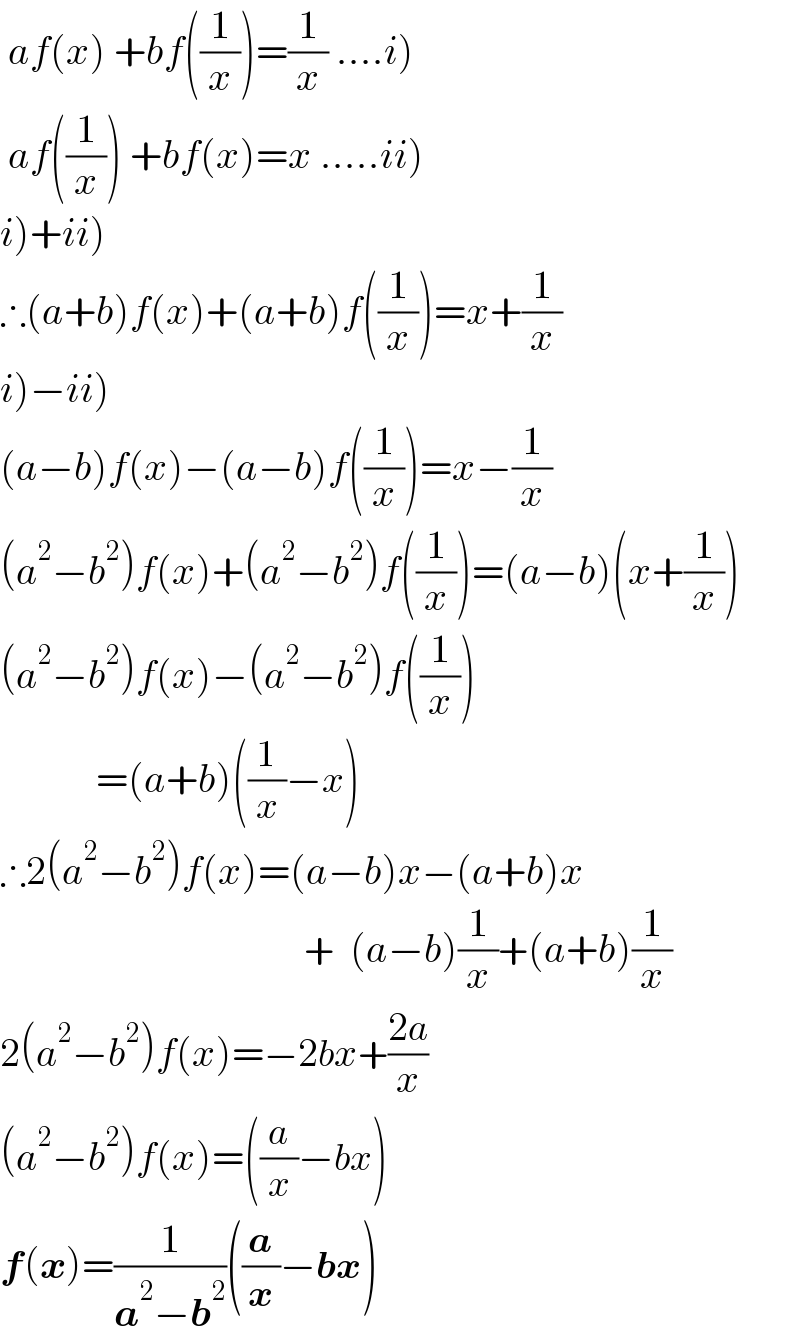
$$\left.\:{af}\left({x}\right)\:+{bf}\left(\frac{\mathrm{1}}{{x}}\right)=\frac{\mathrm{1}}{{x}}\:….{i}\right) \\ $$$$\left.\:{af}\left(\frac{\mathrm{1}}{{x}}\right)\:+{bf}\left({x}\right)={x}\:…..{ii}\right) \\ $$$$\left.{i}\left.\right)+{ii}\right) \\ $$$$\therefore\left({a}+{b}\right){f}\left({x}\right)+\left({a}+{b}\right){f}\left(\frac{\mathrm{1}}{{x}}\right)={x}+\frac{\mathrm{1}}{{x}} \\ $$$$\left.{i}\left.\right)−{ii}\right) \\ $$$$\left({a}−{b}\right){f}\left({x}\right)−\left({a}−{b}\right){f}\left(\frac{\mathrm{1}}{{x}}\right)={x}−\frac{\mathrm{1}}{{x}} \\ $$$$\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right){f}\left({x}\right)+\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right){f}\left(\frac{\mathrm{1}}{{x}}\right)=\left({a}−{b}\right)\left({x}+\frac{\mathrm{1}}{{x}}\right) \\ $$$$\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right){f}\left({x}\right)−\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right){f}\left(\frac{\mathrm{1}}{{x}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\left({a}+{b}\right)\left(\frac{\mathrm{1}}{{x}}−{x}\right) \\ $$$$\therefore\mathrm{2}\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right){f}\left({x}\right)=\left({a}−{b}\right){x}−\left({a}+{b}\right){x} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\:\:\left({a}−{b}\right)\frac{\mathrm{1}}{{x}}+\left({a}+{b}\right)\frac{\mathrm{1}}{{x}} \\ $$$$\mathrm{2}\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right){f}\left({x}\right)=−\mathrm{2}{bx}+\frac{\mathrm{2}{a}}{{x}}\:\: \\ $$$$\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right){f}\left({x}\right)=\left(\frac{{a}}{{x}}−{bx}\right) \\ $$$$\boldsymbol{{f}}\left(\boldsymbol{{x}}\right)=\frac{\mathrm{1}}{\boldsymbol{{a}}^{\mathrm{2}} −\boldsymbol{{b}}^{\mathrm{2}} }\left(\frac{\boldsymbol{{a}}}{\boldsymbol{{x}}}−\boldsymbol{{bx}}\right) \\ $$
Commented by peter frank last updated on 31/Mar/22

$$\mathrm{thank}\:\mathrm{you} \\ $$
Answered by qaz last updated on 31/Mar/22
![af(x)+bf((1/x))=(1/x) ⇒f(x)=(1/(ax))−(b/a)f((1/x)) ⇒f(x)=(1/(ax))−(b/a)[(1/(a∙(1/x)))−(b/a)f((1/(1/x)))] =(1/(ax))−(b/a^2 )x+(b^2 /a^2 )f(x) ⇒f(x)=(((1/(ax))−(b/a^2 )x)/(1−(b^2 /a^2 )))=(((a/x)−bx)/(a^2 −b^2 ))](https://www.tinkutara.com/question/Q167995.png)
$$\mathrm{af}\left(\mathrm{x}\right)+\mathrm{bf}\left(\frac{\mathrm{1}}{\mathrm{x}}\right)=\frac{\mathrm{1}}{\mathrm{x}} \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{1}}{\mathrm{ax}}−\frac{\mathrm{b}}{\mathrm{a}}\mathrm{f}\left(\frac{\mathrm{1}}{\mathrm{x}}\right) \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{1}}{\mathrm{ax}}−\frac{\mathrm{b}}{\mathrm{a}}\left[\frac{\mathrm{1}}{\mathrm{a}\centerdot\frac{\mathrm{1}}{\mathrm{x}}}−\frac{\mathrm{b}}{\mathrm{a}}\mathrm{f}\left(\frac{\mathrm{1}}{\frac{\mathrm{1}}{\mathrm{x}}}\right)\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{ax}}−\frac{\mathrm{b}}{\mathrm{a}^{\mathrm{2}} }\mathrm{x}+\frac{\mathrm{b}^{\mathrm{2}} }{\mathrm{a}^{\mathrm{2}} }\mathrm{f}\left(\mathrm{x}\right) \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{x}\right)=\frac{\frac{\mathrm{1}}{\mathrm{ax}}−\frac{\mathrm{b}}{\mathrm{a}^{\mathrm{2}} }\mathrm{x}}{\mathrm{1}−\frac{\mathrm{b}^{\mathrm{2}} }{\mathrm{a}^{\mathrm{2}} }}=\frac{\frac{\mathrm{a}}{\mathrm{x}}−\mathrm{bx}}{\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} } \\ $$
Commented by peter frank last updated on 31/Mar/22

$$\mathrm{thank}\:\mathrm{you} \\ $$
